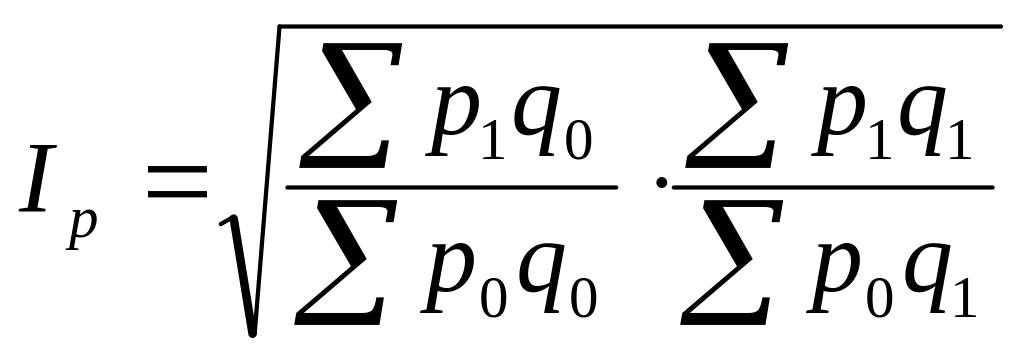- •Содержание
- •Введение
- •Тематический план
- •Планы практических занятий
- •Занятие 7. Тема 4. Обобщающие статистические показатели
- •Общие положения, методический инструментарий и задания на практические занятия по темам
- •Тема 1. Методические основы статистики (2 ч.)
- •Основные положения темы
- •Вопросы и задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 2. Статистическое наблюдение (2 ч.) Основные положения темы
- •Иллюстративный материал темы к вопросу: формы, виды и способы наблюдения
- •Организационные формы
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 3. Сводка и группировка статистических данных (4 ч.) Основные положения темы
- •Методический материал и примеры решения типовых задач к вопросу: сущность и классификация статистических группировок
- •Пример группировки данных
- •Выполнение задания
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 4. Обобщающие статистические показатели (10 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: абсолютные величины Пример расчета условно-натуральных величин
- •К вопросу: относительные величины
- •Пример расчета относительных величин динамики
- •Пример расчета относительных величин планового задания
- •Пример расчета относительных величин выполнения планового задания
- •Пример расчета показателей, основанного на взаимосвязи относительных величин динамики, планового задания и выполнения плана
- •Пример расчета относительной величины структуры
- •Пример расчета относительной величины координации
- •Пример расчета относительной величины сравнения
- •К вопросу: средние величины
- •Пример расчета средних величин по не сгруппированным и сгруппированным данным
- •Пример расчета средней гармонической простой
- •Пример расчета средней гармонической взвешенной
- •Примеры расчета средней геометрической простой
- •Пример расчета средней квадратической
- •Пример применения правила выбора формы средней величины качественного признака
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 5. Анализ рядов распределения (10 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: понятие рядов распределения
- •Пример расчета средней арифметической взвешенной величины методом моментов
- •К вопросу: мода и медиана
- •Пример расчета медианы
- •Пример расчета моды
- •К вопросу: показатели вариации
- •Пример расчета показателей вариации
- •Пример расчета дисперсии методом моментов
- •Пример расчета дисперсии методом разности
- •К вопросу: виды дисперсии. Правило сложения дисперсии. Понятие эмпирического коэффициента детерминации и эмпирического корреляционного отношения
- •Пример расчета общей, межгрупповой и внутригрупповой дисперсии, эмпирического коэффициента детерминации и эмпирического корреляционного отношения
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 6. Анализ концентрации, дифференциации
- •Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: показатели дифференциации распределения
- •Пример расчета квартилей
- •Пример расчета децилей
- •Пример расчета квартильного и децильного коэффициентов
- •К вопросу: показатели концентрации распределения
- •Пример расчета коэффициента концентрации Джини
- •Пример расчета коэффициентов концентрации Герфиндаля и Розенблюта
- •К вопросу: понятие о закономерностях распределения
- •Пример расчета критериев согласия
- •К вопросу: показатели формы распределения
- •Пример расчета показателей формы распределения
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 7. Статистические методы измерения взаимосвязей (8 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: метод сравнения параллельных рядов
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента Фехнера
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена в случае совпадения их значений
- •К вопросу: метод аналитической группировки. Понятие таблиц взаимной сопряженности
- •Пример расчета эмпирического корреляционного отношения
- •Пример оценки степени надежности эмпирического корреляционного отношения с помощью критериев Фишера и Стьюдента
- •К вопросу: показатели тесноты связи между двумя атрибутивными признаками
- •Пример расчета показателей тесноты связи между атрибутивными признаками
- •Пример расчета коэффициента взаимной сопряженности Чупрова
- •К вопросу: понятие корреляционно-регрессионного анализа
- •К вопросу: парная линейная регрессия
- •Пример построения уравнения парной линейной регрессии
- •Пример расчета коэффициентов эластичности
- •Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента
- •К вопросу: понятие многофакторного корреляционно-регрессионного анализа
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 8. Анализ интенсивности динамики (4 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика рядов динамики
- •Пример смыкания рядов динамики данных, отличающихся друг от друга по числу включаемых в исследуемую совокупность единиц
- •Пример смыкания рядов динамики данных, отличающихся друг от друга методикой расчета показателей
- •К вопросу: статистические характеристики рядов динамики
- •Пример расчета показателей интенсивности динамики
- •Пример расчета среднего уровня полного интервального ряда динамики
- •Пример расчета среднего уровня неполного интервального ряда динамики
- •Пример расчета среднего уровня полного моментного ряда динамики
- •Пример расчета среднего уровня неполного моментного ряда динамики
- •Пример расчета средних показателей интенсивности динамики
- •К вопросу: сравнительный анализ рядов динамики
- •Пример сравнительного анализа рядов динамики
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 9. Анализ тенденции развития и колебаний (6 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: структура ряда динамики
- •К вопросу: изучение основной тенденции развития
- •Этапы изучения основной тенденции развития
- •1. Ряд динамики проверяется на наличие тренда
- •2. Производится выравнивание временного ряда
- •Пример проверки ряда динамики на наличие тренда
- •Пример проверки ряда динамики на наличие тренда с помощью метода серий
- •К вопросу: механическое выравнивание рядов динамики Пример механического выравнивания ряда динамики методом укрупненных интервалов
- •Пример механического выравнивания ряда динамики методом скользящей средней
- •К вопросу: аналитическое выравнивание рядов динамики
- •Пример аналитического выравнивания ряда динамики
- •К вопросу: характеристика колеблемости
- •К вопросу: сезонные колебания
- •Пример расчета индексов сезонности при условии отсутствия четко выраженной тенденции изменения уровней ряда динамики
- •Пример расчета индексов сезонности при условии наличия тренда
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 10. Индексный метод (8 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика статистических индексов
- •К вопросу: агрегатный индекс как основная форма общего индекса
- •Пример расчета индивидуальных и агрегатных индексов
- •К вопросу: общие индексы как средние из индивидуальных индексов
- •Пример расчета общих индексов как средних из индивидуальных индексов
- •10.4 Системы взаимосвязанных индексов
- •Пример взаимосвязи индексов и расчета величины абсолютного прироста результативного признака за счет изменения признаков-факторов
- •К вопросу: индексы с постоянной и переменной базой сравнения
- •Пример расчета цепных и базисных индексов физического объема, цен и товарооборота
- •К вопросу: индексы средних величин
- •Пример анализа относительного и абсолютного изменения средних значений качественного признака, в том числе за счет изменения соответствующих факторов
- •К вопросу: территориальные индексы
- •Пример расчета территориальных индексов
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 11. Выборочный метод (4 ч.) Основные положения темы
- •Индивидуальный
- •К вопросу: ошибки выборки
- •Пример расчета ошибок репрезентативности показателей выборки
- •Пример расчета средних ошибок выборки
- •Пример расчета предельных ошибок выборки и доверительных интервалов для характеристик генеральной совокупности
- •К вопросу: определение численности выборки
- •Пример расчета численности выборки, обеспечивающей заданную точность результатов исследования, формируемой посредством случайного бесповторного отбора
- •Пример расчета численности стратифицированной выборки, а также границ, в которых находится среднее значение признака единицы генеральной совокупности
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 12. Представление статистических данных:
- •Основные положения темы
- •Иллюстративный материал темы к вопросу: статистические таблицы
- •К вопросу: классификация статистических графиков
- •Вопросы и задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Список рекомендуемой литературы
- •98309 Г. Керчь, Орджоникидзе, 82
Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика статистических индексов
Индивидуальные индексы обозначаются с помощью буквы i.
Около основания индекса всегда ставится символ того явления, изменение которого изучают. Показатель, изменение которого изучается, называется индексируемым, и его сопровождают знаком 1, если это данные отчетного периода, и 0, если они представлены за базисный период.
Например, индивидуальный индекс физического объема продукции определенного вида (iq), представленный в форме коэффициента, рассчитывается по формуле
 ,
(10.1)
,
(10.1)
где q0 и q1 – соответственно объем конкретного вида продукции базисного и отчетного периодов в натуральных единицах измерения.
Общие (сводные) индексы обозначаются I.
Индекс как относительная величина может быть выражен в виде коэффициентов или процентов.
К вопросу: агрегатный индекс как основная форма общего индекса
При моделировании агрегатных индексов необходимо придерживаться общепринятого в статистике порядка символического обозначения соответствующих явлений, представленного на рис. 10.1.
Для построения общих индексов важно учитывать взаимосвязь приведенных на рис. 10.1 показателей, так:
- pq – стоимость произведенной или реализованной продукции (общий товарооборот);
- zq – общие затраты на производство продукции в денежном выражении;


Рисунок 10.1 - Обозначения показателей, изучаемых с помощью индексов
- zq – общие затраты на производство продукции в денежном выражении;
- tq - общие затраты времени на производство продукции выраженные в трудовых единицах измерения;
- wТ - объем произведенной продукции Q (в натуральном или стоимостном выражении в зависимости от того в каких единицах измерения выражена выработка продукции);
- t = 1/w;
- w = 1/t.
Общий индекс товарооборота (Ipq) рассчитывается по формуле
 ,
(10.2)
,
(10.2)
где p1q1, p0q0 – товарооборот отдельных видов товаров соответственно в отчетном и базисном периодах.
Общий индекс физического объема товарооборота (Iq) рассчитывается по формуле
 .
(10.3)
.
(10.3)
Общий индекс цен (Ip) рассчитывается по формуле
 .
(10.4)
.
(10.4)
По этой же схеме (формулы 10.2-10.4) строятся агрегатные индексы других показателей.
Пример расчета индивидуальных и агрегатных индексов
По данным таблицы 10.1 следует проанализировать динамику физического объема продаж, цен и выручки от реализации (товарооборота) как отдельных видов товаров, так и всей товарной группы бакалейного отдела магазина в 2008 г. по сравнению с 2007 г.
Для определения изменения физического объема продаж и цен отдельных продуктов, реализуемых в бакалейном отделе магазина, а также выручки от их реализации, рассчитаем индивидуальные индексы физического объема, цен и товарооборота в соответствии с методикой, представленной формулой 10.1.
Таблица 10.1 - Данные, характеризующие физический объем и цены реализации
продовольственных товаров в бакалейном отделе магазина в 2007-2008 гг.
Наименование товара |
Продано единиц товаров |
Средняя цена единицы товара, грн. |
||
2007 г. |
2008 г. |
2007 г. |
2008 г. |
|
Сахар, кг Макаронные изделия, кг Крупы, кг Чай, усл. пачки Кофе, усл. банки |
3600 845 1240 1587 726 |
3240 1120 1280 1600 750 |
3,60 2,80 2,50 5,60 10,00 |
4,50 3,00 3,20 5,60 11,00 |
Стоимость продаж (выручка от реализации) каждого вида товаров определяется как произведение физического объема его реализации на цену. Результаты расчетов соответствующих показателей приведены в таблице 10.2.
Таблица 10.2 - Данные, характеризующие динамику продаж товаров в бакалейном отделе
магазина в 2007-2008 гг.
Наименование товара |
Продано единиц товаров |
Средняя цена единицы, грн. |
Стоимость проданных товаров, тыс. грн. |
Индивидуальные индексы, % |
||||||
2007 г. |
2008 г. |
2007 г. |
2008 г. |
2007 г. |
2008 г. |
2008 г. в ценах 2007 г. |
физического объема |
цен |
стоимости продаж |
|
q0 |
q1 |
p0 |
p1 |
p0q0 |
p1q1 |
q1p0 |
iq |
ip |
iqp |
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Сахар, кг Макаронные изделия, кг Крупы, кг Чай, усл. пачки Кофе, усл. банки |
3600
845 1240 1587 726 |
3240
1120 1180 1600 750 |
3,60
2,80 2,50 5,60 10,00 |
4,50
3,00 3,20 5,60 11,00 |
12,960
2,366 3,100 8,887 7,260 |
14,580
3,360 3,776 8,960 8,250 |
11,664
3,136 2,950 8,960 7,500 |
90,0
132,5 95,2 100,8 103,3 |
125,0
107,1 128,0 100,0 110,0 |
112,5
142,0 121,8 100,8 113,6 |
Всего |
х |
х |
х |
х |
34,573 |
38,926 |
34,210 |
х |
х |
х |
Данные столбца 8 таблицы 10.2 свидетельствуют о том, что в 2008 г. по сравнению с 2007 г. физический объем продаж макаронных изделий, кофе и чая увеличился соответственно на 32,5 % (132,5 - 100,0), 3,3 % (103,3 – 100,0) и 0,8 % (100,8 -100,0). В то же время, в анализируемом периоде отмечается уменьшение физического объема продаж сахара на 10,0 % (90,0 - 100,0) и круп на 4,8 % (95,2 – 100,0).
По данным столбца 9 таблицы 10.2 видно, что цены практически на все виды товаров в исследуемом периоде увеличились соответственно на 25,0 % (сахар); 7,1 % (макаронные изделия); 28,0 % (крупы) и 10,0 % (кофе). Исключение составили только цены на чай, сохранившиеся в 2008 г. на уровне 2007 г.
Объемы продаж каждого вида товаров в стоимостном выражении возросли соответственно на 12,5 %; 42,0 %; 21,8 %; 0,8 %; 13,6 % (по данным столбца 10 таблицы10.2).
Для характеристики динамики физического объема продаж, цен на продукты питания и товарооборота в целом по бакалейному отделу магазина в 2008 г. по сравнению с 2007 г. исчислим соответствующие общие индексы.
Общий
индекс физического объема товарооборота,
рассчитанный по формуле 10.3 на основе
итоговых данных 7 и 5 столбцов таблицы
10.2, равен:
![]() %,
что свидетельствует о снижении общего
физического объема реализации продукции
бакалейного отдела в 2008 г. по сравнению
с 2007 г. на 1,05 % (98,95 -
100).
%,
что свидетельствует о снижении общего
физического объема реализации продукции
бакалейного отдела в 2008 г. по сравнению
с 2007 г. на 1,05 % (98,95 -
100).
Общий
индекс цен, рассчитанный по формуле
10.4 на основе итоговых данных 6 и 7 столбцов
таблицы 10.3, равен:
![]() %,
т. е. в 2008 г. по сравнению с 2007 г. цены на
продукцию бакалейного отдела возросли
на 13,8 % (113,8-100).
%,
т. е. в 2008 г. по сравнению с 2007 г. цены на
продукцию бакалейного отдела возросли
на 13,8 % (113,8-100).
Общий
индекс товарооборота, рассчитанный по
формуле 10.2 на основе итоговых данных
5 и 6 столбцов таблицы 10.2, равен:
![]() %,
что свидетельствует о росте объема
реализации товаров (товарооборота)
бакалейного отдела в 2008 г. по сравнению
с 2007 г. на 12,6%.
%,
что свидетельствует о росте объема
реализации товаров (товарооборота)
бакалейного отдела в 2008 г. по сравнению
с 2007 г. на 12,6%.
Агрегатные индексы физического объема товарооборота и цен Леспейреса, Пааше и Фишера показаны в таблице 10.3.
Таблица 10.3 – Агрегатные индексы физического объема товарооборота и цен
Леспейреса, Пааше и Фишера
Формула |
Агрегатные индексы |
|||
физического объема товарооборота |
№ формулы |
цен |
№ формулы |
|
Леспейреса |
|
10.5 |
|
10.6 |
Пааше |
|
10.7 |
|
10.8 |
Фишера |
|
10.9 |
|
10.10 |