К вопросу: показатели вариации

Размаха вариации (R) рассчитывается по формуле

, (5.5)

где Х_max и Х_min – соответственно максимальное и минимальное значения признака в исследуемой совокупности.

Среднее линейное отклонение ( ) по не сгруппированным данным рассчитывается по формуле

. (5.6)

Среднее линейное отклонение ( ) по сгруппированным данным рассчитывается по формуле

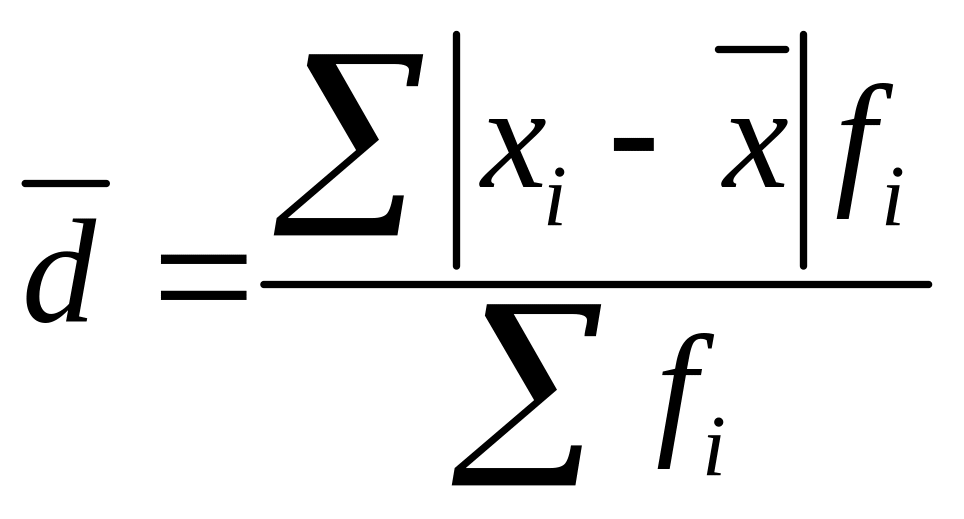. (5.7)

Дисперсия (σ²) по не сгруппированным данным рассчитывается по формуле

. (5.8)

Дисперсия (σ²) по сгруппированным данным рассчитывается по формуле

. (5.9)

Среднее квадратическое отклонение (σ) рассчитывается по формуле

. (5.10)

Коэффициент вариации (V) рассчитывается по формуле

. (5.11)

Следует помнить, что оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава. Так, для совокупности сельхозпредприятий вариация урожайности в одном и том же природном регионе может быть оценена как слабая, если V < 10 %, умеренная при 10 % < V <25 % и сильная при V > 25 %. Напротив, вариация роста в совокупности взрослых мужчин или женщин уже при коэффициенте, равном 7 %, должна быть оценена и восприниматься людьми как сильная. Таким образом, оценка интенсивности вариации состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив. Если различия в урожайности, заработной плате или доходе на душу населения в несколько и даже в десятки раз воспринимаются как вполне естественные, то различия роста людей хотя бы в полтора раза уже воспринимаются как очень сильные.

Пример расчета показателей вариации

По данным таблицы 5.5 необходимо охарактеризовать ряд распределения работников предприятия по заработной плате на предмет его однородности и типичности среднего значения уровня заработной платы для работников предприятия.

По формуле 5.5 размах вариации R = 2000 – 800 = 1200 грн., т.е. разница между максимальным и минимальным уровнем оплаты труда на предприятии составляет приблизительно 1200 грн. На первый взгляд это достаточно большой разброс в оплате труда работников предприятия, т. е. исследуемая совокупность не однородна по оплате труда. Данное предположение подтвердится или нет последующими расчетами. Отметим, что верхнюю границу последнего открытого интервала определили исходя их величины смежного с ним интервала, которая равна 200 грн. (1800 - 1600), 1800 + 200 = 2000 грн.

Расчет среднего линейного отклонения проведем с помощью данных таблицы 5.9. Напомним, что средняя заработная плата работников предприятия, исчисленная по формулам 4.21 и 5.1 равна 1340 грн.

Таблица 5.9 - Данные для расчета среднего линейного отклонения

заработной платы работников предприятия

Группы работников по уровню заработной платы, грн.	Число работников, чел. (fi)	Середина интервала, грн. (xi)	= = | xi - 1340|
800 -1000 1000 -1200 1200 - 1400 1400 - 1600 1600 - 1800 1800 и выше	20 80 160 90 40 10	900 1100 1300 1500 1700 1900	440 240 40 160 360 560	8800 19200 6400 14400 14400 5600
Всего	400	-	-	68800

По формуле 5.7 среднее линейное отклонение грн.

Расчет дисперсии (среднего квадрата отклонений) проведем с помощью данных таблицы 5.10.

Таблица 5.10 - Данные для расчета среднего квадрата отклонений

заработной платы работников предприятия

Группы работников по уровню заработной платы, грн.	Число работников, чел. (fi)	Середина интервала, грн. (xi)
800 -1000 1000 -1200 1200 - 1400 1400 - 1600 1600 - 1800 1800 и выше	20 80 160 90 40 10	900 1100 1300 1500 1700 1900	193600 57600 1600 25600 129600 313600	3872000 4608000 256000 2304000 5184000 3136000
Всего	400	-	-	19360000

По формуле 5.9 дисперсия .

По формуле 5.10 среднее квадратическое отклонение грн.

На основании полученных показателей вариации пока еще трудно оценить однородность работников предприятия по уровню их заработной платы.

По формуле 5.11 коэффициент вариации , что говорит о достаточной однородности исследуемой совокупности по уровню зарплаты и типичности ее среднего уровня.

Математические свойства дисперсии, упрощающие технику ее расчета:

1) если от всех вариант ряда распределения отнять какое-то постоянное число А, то дисперсия от этого не изменится.

2) если все значения вариант разделить на какое-то постоянное число h, то дисперсия уменьшится от этого в h² раз, а среднее квадратическое отклонение – в h раз.

Эти свойства положены в основу расчета дисперсии способом моментов. Способ моментов применим в том случае, если задан интервальный ряд с равными интервалами.

Дисперсия методом моментов рассчитывается по формуле

, (5.12)

где h – шаг интервала;

m´, m´´- соответственно моменты первого и второго порядка. Напомним, что момент первого порядка рассчитывается по формуле 5.2. Момент второго порядка рассчитывается по формуле

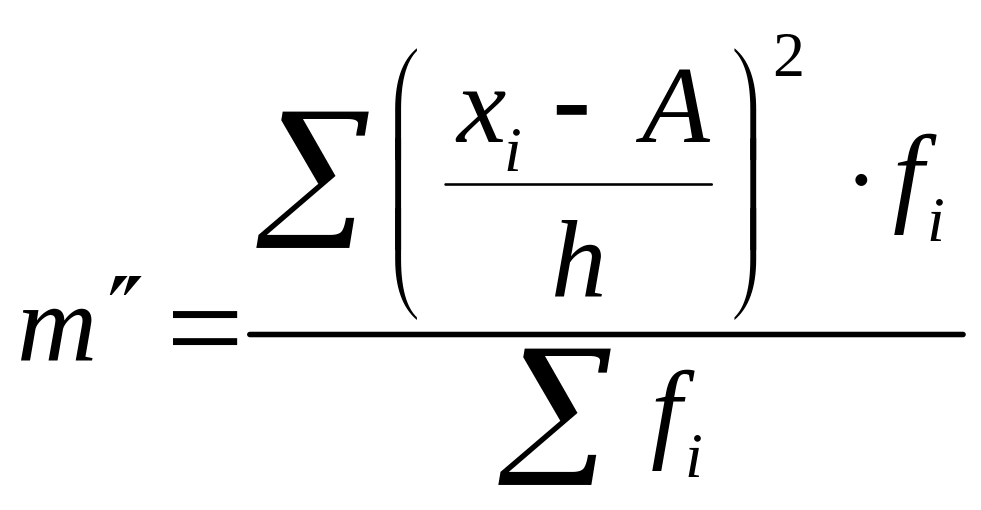. (5.13)