Примеры решения задач.

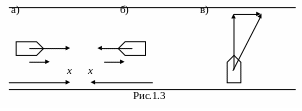
1. Найти скорость относительно берега реки: а) лодки, идущей по течению; б) лодки, идущей против течения; в) лодки, идущей под углом α = 90⁰к течению. Скорость течения реки u = 1 м/с, скорость лодки относительно воды υ₀ = 2 м/с.

Р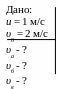 ешение.

а). или в проекции на ось х: .

б). или в проекции на ось х: .

в). . Сложив вектора по правилу треугольников, получим:

.

Ответ: υ_а = 3 м/с; υ_б = 1 м/с; υ_в = 2,24 м/с.

2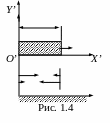 . Колонна мотоциклистов движется по шоссе со скоростью υ = 10м/с, растянувшись на расстояние l = 5км. Их хвоста и головы колонны одновременно выезжают навстречу друг другу два мотоциклиста со скоростями υ₁ = 20м/с и υ₂ = 15м/с соответственно. За какое время первый мотоциклист достигнет головы, а второй – хвоста колонны?

Р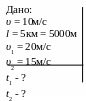 ешение.

I способ. Движущуюся систему отсчёта свяжем с колонной. За начало координат O’ примем хвост колонны, а за положительное направление оси O’ X’ - направление движения колонны.

Неподвижную систему отсчёта свяжем с Землёй, начало координат совместим с точкой, где находился хвост колонны в момент выезда мотоциклистов, положительное направление оси такое же, как и оси O’ X’. Обозначим через и скорости первого и второго мотоциклистов в движущейся системе отсчёта.

Согласно закону сложения скоростей, , , откуда:

.

Найдём проекции векторов и на ось O’ X’, учитывая при этом, что проекция разности векторов равна разности их проекций (на одну и туже ось):

или

Запишем уравнение, выражающее зависимость координаты первого мотоциклиста от времени t:

(1)

В момент времени t = t₁ мотоциклист достигнет головы колонны; его координата x’₁ = l. На основании уравнения (1) получим , откуда

(2)

Зависимость координаты второго мотоциклиста от времени выразится уравнением

(3)

В момент времени t = t₂ второй мотоциклист достигнет хвоста колонны, координата которого x’₂ = 0. Согласно уравнению (3) получим , откуда:

(4)

По формулам (2) и (4) найдём с и с

II способ. Эту задачу можно решить иначе. Рассматривая движение колонны мотоциклистов относительно неподвижной системы, отсчёта запишем уравнения для координат первого x₁ и второго x₂мотоциклистов, а также для координат головы x₃ и хвоста x₄ колонны:

В момент времени t = t₁, когда мотоциклист достигнет головы колонны, будет иметь место равенство x₁ = x₃, т.е.

В момент времени t = t₂ второй мотоциклист достигнет хвоста колонны, при этом x₂ = x₄. Следовательно

Таким образом, независимо от выбора системы отсчёта результат получается один и тот же.

Ответ: с и с.

3. Радиус-вектор, характеризующий положение частицы М относительно неподвижной точки О, меняется со временем по закону , где А и В - постоянные векторы, причем ; ω - положительная постоянная. Найти ускорение а частицы и уравнение ее траектории y(x), взяв оси х и у совпадающими по направлению с векторами А и В соответственно и имеющими начало в точке О.

Р ешение.

Продифференцировав по времени дважды, по­лучим

,

т. е. вектор а все время направлен к точке О, а его модуль пропор­ционален расстоянию частицы до этой точки.

Т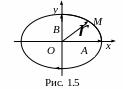 еперь найдем уравнение траектории. Спроецировав на оси х и у, получим

,

Исключив ωt из этих двух уравнений, найдем

.

Это уравнение эллипса, А и В - его полуоси (рис. 1.5) , где стрелкой показано направление движения частицы М).

Ответ: ; .

4. Точка движется замедленно по окружности радиуса r так, что ее тангенциальное и нормальное ускорения в каждый момент равны друг другу по моду­лю. В начальный момент точке была сообщена скорость υ₀. Найти скорость υ и модуль полного ускорения а точки в зависимости от пройденного пути S.

Р ешение.

По условию, . Представив dt как , преобразуем исходное уравнение к виду

.

Интегрирование этого уравнения с учетом начальной скорости при­водит к следующему результату:

,

В данном случае , поэтому полное ускорение , или

Ответ: ; .

5. Движение материальной точки задано уравнением . Определить момент времени, в который скорость точки равна нулю. Найти координату и ускорение точки в этот момент. Построить графики координаты, пути, скорости и ускорения этого движения от времени.

Р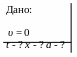 ешение.

В озьмём первую производную от уравнения движения точки и, получив уравнение скорости, приравняем его к нулю и определим время: с. Ускорение найдём, взяв первую производную от уравнения скорости: м/с ². Подставив время в уравнение пути, получим: м. Построим графики (рис. 1.6).

Ответ: t = 40с; a = -0,1м/с ²; x = 80м.