Основные определения и формулы.

Кинематика - раздел механики, изучающий геометрические свойства движения тел без учета их масс и действующих на них сил.

Материальная точка - это тело, размеры и форма которого несущественны в рассматриваемой задаче.

Движение материальной точки считается заданным, если известно её положение относительно выбранной системы отсчета в любой момент времени.

Совокупность жестко связанных тела отсчета, системы координат и отсчитывающих время часов называется системой отсчета (с.о).

Основная задача кинематики - установление способов задания движения точек или тел и определение соответствующих кинематических характеристик этих движений.

Отношение вектора перемещения ко времени называется вектором средней скорости.

. (1.1)

Величина мгновенной скорости прохождения пути определяется по формуле

(1.2)

Ускорение – физическая векторная величина, характеризующая быстроту изменения вектора скорости движения материальной точки по числовому значению и по направлению.

Средним ускорением неравномерного движения называется векторная величина, равная отношению изменения вектора скорости к интервалу времени t за которое произошло это изменение.

(1.3)

Мгновенным ускорением называется векторная величина равная первой производной скорости по времени или вторая производная радиус – вектор по времени

(1.4)

Для нахождения мгновенного ускорения его раскладывают на две составляющие: тангенциальное (или касательное) и центростремительное (или нормальное) _n (рис. 1.1).

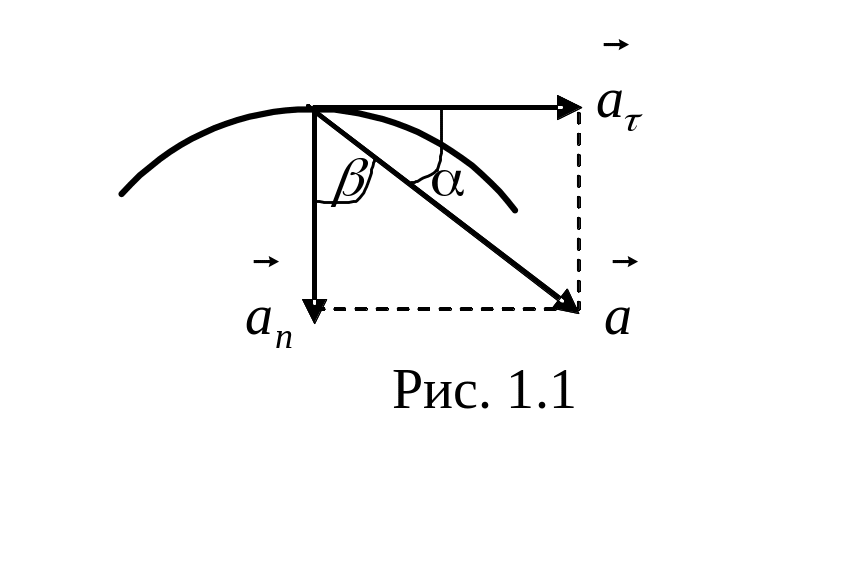
Касательное ускорение характеризует изменение скорости по величине в единицу времени, оно направлено по касательной к траектории. Величина касательного ускорения определяется по формуле:

. (1.5)

Нормальное ускорение характеризует изменение скорости по направлению в единицу времени, оно направленно к центру кривизны траектории по радиусу и выражается формулой

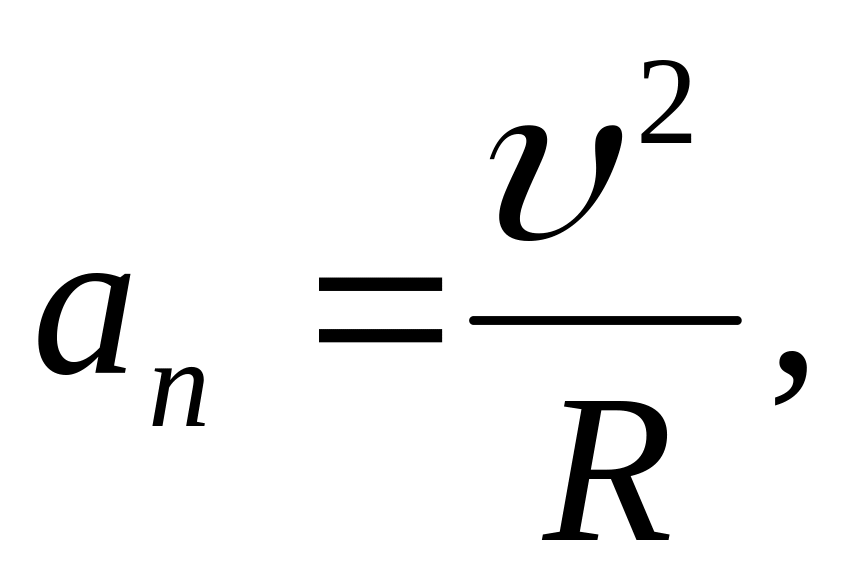(1.6)

где R - радиус кривизны траектории в данной точке.

Величина полного ускорения

(1.7)

Г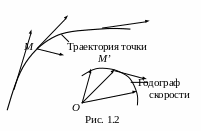 одограф в механике, кривая, представляющая собой геометрическое место концов переменного (изменяющегося со временем) вектора, значения которого в разные моменты времени отложены от общего начала О (рис 1.2). Он даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого изменения, имеющей направление касательной к годографу. Например, скорость точки является величиной, изображаемой переменным вектором . Отложив значения, которые имеет вектор в разные моменты времени, от начала О, получим годограф скорости; при этом величина, характеризующая быстроту изменения скорости в точке М, т. е. ускорение (в этой точке, имеет для любого момента времени направление касательной к годографу скорости в соответствующей его точке (М’).