29. Повторная и бесповторная выборка

При повторном отборе каждая единица, отобранная в случайном порядке из генеральной совокупности, после проведения наблюдения возвращается в эту совокупность и может быть вновь подвергнута обследованию. На практике такой способ от­бора встречается редко. Гораздо более распространен собственно случайный бесповторный отбор, при котором обследованные еди­ницы в генеральную совокупность не возвращаются и не могут быть обследованы повторно. При повторном отборе вероятность попадания в выборку для каждой единицы генеральной совокуп­ности остается неизменной. При бесповторном отборе она меня­ется, но для всех единиц, оставшихся в генеральной совокупнос­ти после отбора из нее нескольких единиц, вероятность попадания в выборку одинакова.

29. Средняя ошибка выборки

Средняя ошибка выборки — это среднее квадратическое откло­нение всех возможных значений выборочной средней от генераль­ной средней, т.е. от своего математического ожидания.

Дисперсия возможных значений выборочной средней

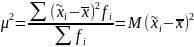
В математической статистике доказано, что эта величина в п раз меньше дисперсии в генеральной совокупности. В данном при­мере дисперсия в генеральной совокупности σ²_г = 0,5, а объем выборки n = 2, тогда Следовательно, средняя ошибка выборки может быть опреде­лена по формуле .

При собственно случайном повторном отборе средняя ошибка выборки зависит от:

• вариации изучаемого признака в генеральной совокупности:

• объема выборки.

Чем больше вариация признака, тем больше ошибка выборки. Для ее уменьшения необходимо увеличить объем выборочной со­вокупности.

В действительности решается обратная задача: на основе вы­борочных данных делается вывод о некоторых характеристиках генеральной совокупности. 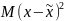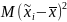Согласно правилу сложения диспер­сий дисперсия в генеральной совокупности может быть представлена как сумма двух слагаемых: средней величины из от­клонений отдельных значений от выборочных средних и средней величины из отклонений выборочных средних от гене­ральной средней т.е.

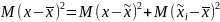
Учитывая что 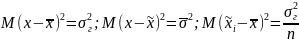получим 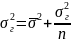или 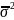= 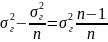где средняя дисперсия выборочных совокупностей

Следовательно 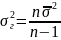. В таком случае средняя ошибка выборки

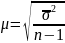
Так как все возможные значения дисперсии в выборочной со­вокупности неизвестны, при нахождении средней ошибки выбор­ки вместо σ² в формуле используют дисперсию конкретной выборки σ². При такой замене велика вероятность малой погреш­ности. При достаточно большом объеме выборочной совокупно­сти в формуле вместо (п — 1) можно использовать величину п. Таким образом, средняя ошибка выборки при собственно случай­ном повторном отборе будет рассчитываться по формуле .

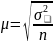29. Предельная ошибка выборки.

Отклонение выборочной харак­теристики от генеральной называется предельной ошибкой выборки А. Она определяется в долях средней ошибки с заданной вероятно­стью, т.е. 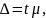где t — коэффициент доверия, зависящий от вероятности, с ко­торой определяется предельная ошибка выборки. Вероятность появления определенной ошибки выборки нахо­дят с помощью теорем теории вероятностей. Согласно теореме П.Л. Чебышёва, при достаточно большом объеме выборки и ограни­ченной дисперсии генеральной совокупности вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:

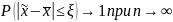
A.M. Ляпунов доказал, что независимо от характера распреде­ления генеральной совокупности при увеличении объема выборки рас­пределение вероятностей появления того или иного значения выбо­рочной средней приближается к нормальному распределению. (Это так называемая центральная предельная теорема.) Следователь­но, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошиб­ки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:

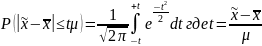- нормированное отклонеие выборочной средней от генеральной средней