19. Эксцесс распределения (куртозис, Ex)

Для нормального распределения 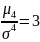поэтому для оценки крутизны данного распределения в сравнении с нормальным вы­числяется эксцесс распределения

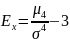
20. Сглаживание эмпирического распределения нормальным законно распределения

При построении статистических моделей весьма широко при­меняется нормальное распределение.

Распределение непрерывной случайной величины х называют нормальным N(x, с), если соответствующая ей плотность распре­деления выражается формулой:

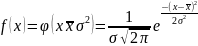или

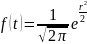
где 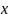- значение изучаемого признака

- средняя арифметическая ряда

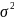- дисперсия значений изучаемого признака

- среднее квадратическое отклонение изучаемого признака

= 3.1415

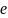= 2.7182

- нормированное отклонение

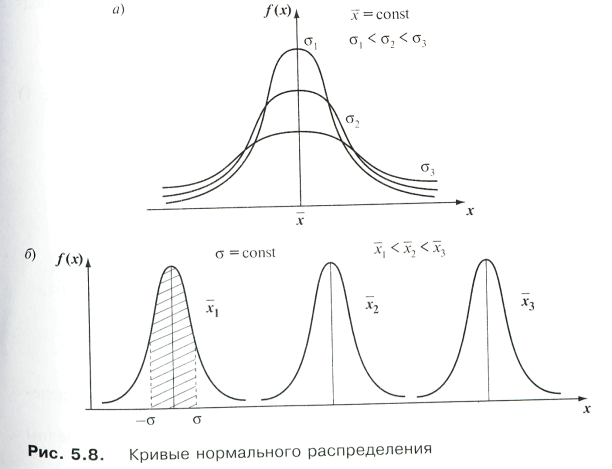
При графическом изображении плотности распределения f(x) получим кривую нормального распределения, симметричную от­носительно вертикальной прямой х= х (рис. 5.8), поэтому вели­чину х называют центром распределения.

Случайные величины, распределенные по нормальному зако­ну, различаются значениями параметров х и а, поэтому очень важно выяснить, как эти параметры влияют на вид нормальной

кривой.

Если х не меняется, а изменяется только а, то:

1) чем меньше о, тем более вытянута вверх кривая (см. рис. 5.8, а), а так как площадь, ограниченная осью х и данной кривой, рав­на 1, то вытягивание вверх компенсируется сжатием около центра распределения х и более быстрым приближением кри­вой к оси абсцисс;

2) чем больше о, тем более плоской и растянутой вдоль оси аб­сцисс становится кривая.

Если а остается неизменной, а х изменяется, то кривые нор­мального распределения имеют одинаковую форму, но отличаются друг от друга положением максимальной ординаты (см. рис. 5.8, б).

21. Понятие статистической гипотезы и статистического критерия, как инструмента проверки статистических гипотез

Результаты выборочных наблюдений широко используются в статистике для проверки предположений, выдвигаемых в отноше­нии характера или параметров распределения случайной величины в генеральной совокупности. Такие предположения, которые пла­нируется проверить с помощью специальных статистических мето­дов, называются статистическими гипотезами.

Проверка статистической гипотезы заключается в том, чтобы оценить, можно ли считать случайным расхождение между вы­двинутой гипотезой и результатами выборочного наблюдения. Такая оценка всегда носит вероятностный характер. Если расхож­дение между эмпирическими и теоретическими значениями не выходит за пределы случайной ошибки, то можно считать, что с заданной вероятностью выдвинутая гипотеза не опровергается. При этом справедливость самой гипотезы не доказывается, а лишь делается вывод о том, можно ли ее считать допустимой или необ­ходимо отвергнуть.

Например, для санитарного контроля проводится мониторинг, в ходе которого устанавливается степень соответствия фактическо­го содержания вредных веществ в атмосфере предельно допусти­мой концентрации (ПДК). Обозначим ПДК какого-либо вредного вещества, например двуокиси углерода, через х₀, а фактическую концентрацию, установленную в результате мониторинга, через х. Требуется проверить справедливость гипотезы о том, что содержа ние вредного вещества в атмосфере города можно признать допу­стимым. Если эта гипотеза не подтверждается, т.е. окажется, что х > х₀, то необходимы дополнительные меры по охране атмосфер­ного воздуха.

Проверяемая гипотеза называется основной и обозначается че­рез Н_0. Суть проверки — убедиться в отсутствии систематической ошибки между исследуемым параметром генеральной совокупно­сти и заданным его значением, т.е. проверяется гипотеза о нуле­вом расхождении между ними, поэтому основную гипотезу назы­вают также нулевой.

При записи содержание гипотезы отделяется от символа Н₀ двоеточием. В приведенном примере суть проверяемой гипотезы может быть представлена следующим образом:

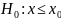
Гипотеза, альтернативная основной, обозначается через Н.. В нашем случае альтернативной является гипотеза о том, что со­держание вредного вещества в атмосфере города превышает ПЛК. Т.е.

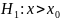
Выдвигаемые гипотезы могут быть простыми и сложными. Простая гипотеза однозначно характеризует оцениваемый пара­метр генеральной совокупности. Например, Н₀: х = х₀, т.е. сте­пень загрязнения воздуха точно соответствует ПДК. Сложная ги­потеза определяет область возможных значений исследуемого параметра. Так. выдвинутая ранее гипотеза Н₀: х < х. является сложной.