
Вопрос №1
Матрицы и многомерные векторы. Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.
Виды матриц.
Две матрицы называются равными, если их соответствующие элементы равны.
Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.
Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.
Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.
Матрица, состоящая из одних нулей, называется нулевой.
Если в квадратной матрице все элементы стоящие ниже (выше) главной диагонали равны 0, то она называется верхний (нижний) треугольник.
Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться транспонированной к матрице А.
Если матрица А равна транспонированной, то она называется симметричной.
Вопрос №3
Перестановки. Расположение n элементов набора в произвольном порядке называется перестановка. Транспозицией называется перестановка двух каких либо элементов. Инверсией в перестановке называется наличие пары чисел, в которое большее число предшествует меньшему. Если число инверсий в перестановке честное, то она называется четной и наоборот.
Определитель произвольного порядка. Определителем квадратной матрицы n-го порядка, называется число равное алгебраической сумме n факториал слагаемых, каждый из которых является произведением n элементов матрицы взятых по одному из каждой строки и столбца, при этом каждое слагаемое умножается на (-1) в степени число инверсий в перестановке j если первые индексы взяты в порядке нарастания.
Вопрос №2
Определители 2-го и 3-го порядка и их свойства. Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае - матрица вырожденная или особая.
Определителем квадратной матрицы 2-го порядка, называется число равное разности произведений элементов главной и побочной диагонали матрицы.
О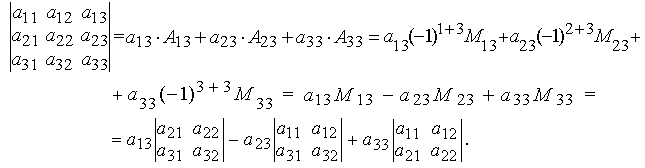 пределителем
квадратной матрицы3-го
порядка,
называется число равное:
пределителем
квадратной матрицы3-го
порядка,
называется число равное:
Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.
Свойства определителей:
1) Если строка (столбец) матрицы состоит из 0, то ее определитель равен 0.
2) Если все элементы, какой либо строки (столбца) матрицы умножить на одно и тоже число, то и ее определитель умножится на это же число.
3) При транспонировании матрицы ее определитель не меняется.
4) При перестановки, каких либо двух строк (столбцов) матрицы знак матрицы меняется на противоположный. Доказательство вытекает из того, что при перестановке одной транспозиции четность инверсии меняется.
5) Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.
6) Сумма произведений элементов, какой либо строки (столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.
7) Если элементы, какой либо строки (столбца) равны сумме двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая k-строка (столбец) в первом определителе содержит первые слагаемые, во втором вторые.
8) Определитель матрицы не изменится если к элементам какой либо строки (столбца) прибавить элемент какой либо строки (столбца) предварительно умноженные на одно и то же число.
