45. Выбор формы зависимости между переменными. Метод наименьших квадратов

Одна из наиболее общих задач статистики состоит в определении формы и оценивании связи между переменными Х и Y (если такая связь существует). Если имеется n пар наблюдений над такими переменными, то наблюдения можно представить точками на плоскости, получая так называемую диаграмму (или поле) рассеяния. Затем можно постараться подобрать некоторую гладкую кривую таким образом, чтобы она располагалась как можно «ближе» к этим точкам. Особенность задачи состоит в том, чтобы наличие случайных возмущений делает бесполезным подбор такой функции, которая точно описывала бы опытные значения, т.е. график искомой функции не должен обязательно проходить через все точки диаграммы рассеяния. Другими словами, требуется как можно точнее отразить общую тенденцию зависимости Y от Х, сглаживая при этом случайные возмущения.

Для решения поставленной задачи часто применяется метод наименьших квадратов. Этот метод дает возможность при заданном виде зависимости переменных выбрать ее параметры (коэффициенты) так, чтобы получаемая кривая в некотором смысле наилучшим образом отображала экспериментальные данные.

Весьма часто вопрос о типе зависимости между переменными Х и Y решается по внешнему виду поля рассеяния. Например, экспериментальные точки, изображенные на первом из двух представленных ниже рисунков, явно наводит на мысль о линейной зависимости вида , где и b – некоторые постоянные величины, – случайная переменная, характеризующая отклонение от теоретической кривой. Квадратичная зависимость, изображенная на втором рисунке, хорошо может быть представлена многочленом второй степени .

Предположим, что исходя из некоторых соображений, выбран вид зависимости , где – неизвестные параметры, – случайная переменная, характеризующая отклонение от теоретической кривой. Требуется так выбрать параметры , чтобы кривая «наилучшим» образом отображала зависимость, полученную в опыте.

Метод наименьших квадратов выбора сглаживающей кривой состоит в том, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум. Другими словами, требуется выбрать параметры так, чтобы функция

достигала минимума.

Если функция имеет частные производные по всем параметрам , то необходимое условие минимума функции представляет собой систему уравнений с m неизвестными:

Контрольные вопросы

1. Как определяется зависимость между признаками: а) функциональная; б) вероятностная; в) корреляционная?

2. В чем заключается задача: а) корреляционного анализа; б) регрессионного анализа?

3. Что называется диаграммой рассеяния или корреляционным полем?

4. Для каких целей используется диаграмма рассеяния?

5. В чем состоит сущность метода наименьших квадратов?

46. Коэффициент корреляции и проверка его значимости. Линейная регрессия и прогноз

В п. 29 – 32 были даны определения теоретического коэффициента корреляции и коррелированных величин, перечислены свойства коэффициента корреляции.

Точечной оценкой теоретического коэффициента корреляции является выборочный коэффициент корреляции , который находится по формуле:

,

где и – выборочные средние; , – выборочные средние квадратические отклонения переменных Х и Y соответственно; – выборочное среднее значение переменной .

Можно показать, что выборочный коэффициент корреляции обладает всеми свойствами теоретического коэффициента корреляции, т.е.

1. Для любых переменных Х и Y абсолютная величина коэффициента корреляции не превосходит единицы, т.е. ;

2. Если Х и Y независимы, то 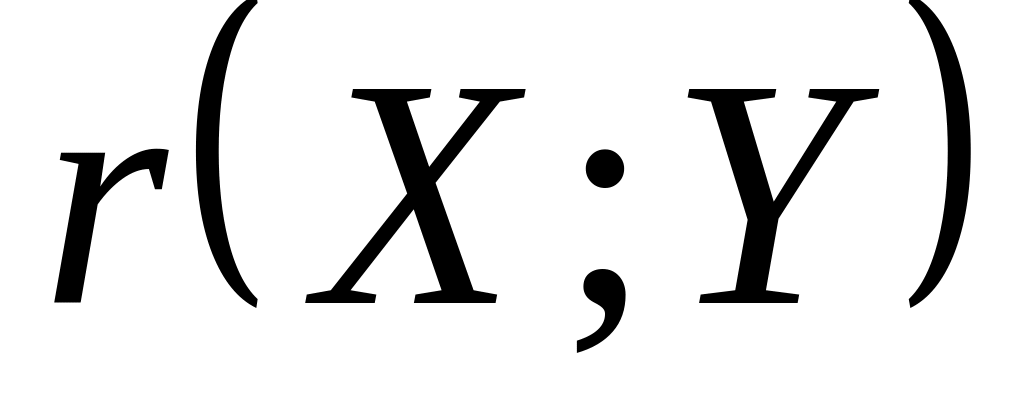= 0;

3. Абсолютная величина коэффициента корреляции равна единице тогда и только тогда, когда между переменными Х и Y существует линейная связь, т.е. , где и b – некоторые постоянные величины. При этом = 1, если a>0, и = -1, если a<0.

В силу всего сказанного выше, можно заключить, что изучение вида линейной зависимости между переменными Х и Y имеет смысл лишь тогда, когда величина значима или существенна, т.е. не очень близка к нулю. Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между переменными, полученное по выборочным данным, в известной мере может быть распространено и на генеральную совокупность. Для достижения этой цели может быть использован критерий, основанный на распределении Стьюдента.

Для оценки достоверности коэффициента корреляции проверяется гипотеза Н₀ об отсутствии линейной корреляционной связи между переменными в генеральной совокупности (против альтернативной гипотезы, состоящей в том, что зависимость между Х и Y значима), т.е. Н₀: , по следующей схеме:

1. Вычисляется статистика 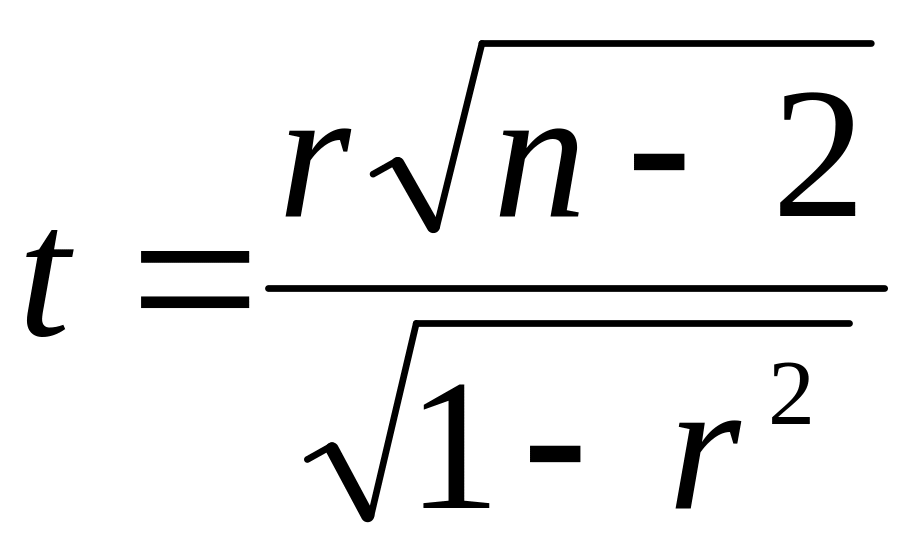отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции , где n – число наблюдений;

2. По таблице критических точек распределения Стьюдента на уровне значимости и при числе степеней свободы находим значение ;

3. Если не выполняется неравенство , гипотеза Н₀ отвергается, т.е. выборочный коэффициент корреляции существенно отличается от нуля, что свидетельствует о достоверности коэффициента корреляции.

Задача. Выборочный коэффициент корреляции между переменными Х и Y при числе наблюдений n = 50 оказался равным 0,74. Оценить достоверность коэффициента корреляции на 5% уровне значимости.

Решение. Найдем статистику критерия по формуле :

.

Для уровня значимости и числа степеней свободы , находим критическое значение статистики . Поскольку , то коэффициент корреляции достоверен на 5% уровне значимости.

Как было отмечено в п. 32, при линейной зависимости между переменными Х и Y уравнение регрессии Y на Х представляет собой прямую

,

где а и b – неизвестные коэффициенты.

Исходя из выборочных данных, методом наименьших квадратов находят следующие оценки неизвестных коэффициентов уравнения:

,

,

где , , , , r определяются формулами, приведенными в предыдущих разделах.

Оценкой теоретической прямой регрессии является выборочная прямая регрессии

.

Чтобы подчеркнуть, что речь идет о выборочном условном среднем, прямую, определяемую последним уравнением, обозначают .

Точность линейной аппроксимации выборочных данных визуально можно оценить, сравнив поле рассеяния с графиком выборочной прямой регрессии.

Наилучший точечный линейный прогноз среднего значения зависимой переменной Y при любом фиксированном значении независимой переменной Х = х₀ задается при помощи выборочного уравнения регрессии Y на Х:

.

Задача 2. В детской поликлинике была собрана следующая информация о связи между временем реакции ребенка Y и его возрастом (в месяцах) X:

Возраст (мес.)	1	2	3	4
Время реакции (сек)	1,5	0,8	0,5	0,4

Используя полученные данные, необходимо вычислить выборочный коэффициент корреляции, проанализировать степень тесноты и направление связи между изучаемыми переменными. Предскажите время реакции ребенка в возрасте 4,5 месяца.

Решение. По данным таблицы найдем выборочные средние и среднее квадратические отклонения переменных Х и Y:

Вычислим выборочное среднее значение величины :

.

Выборочный коэффициент корреляции найдем по формуле:

Полученное значение выборочного коэффициента корреляции показывает, что между переменными Х и Y существует достаточно тесная связь, близкая к линейной. Поскольку , то эта связь убывающая, т.е. по мере увеличения возраста, уменьшается время реакции ребенка.

Выборочное уравнение линейной регрессии Y на Х будем искать в виде:

,

и в данной задаче оно таково:

.

Подставляя в последнее соотношение значение х = 4,5 (мес.), найдем ожидаемое время реакции ребенка:

(сек).