10. Локальная формула Муавра-Лапласа. Формула Пуассона

Очевидно, что пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий с очень большими числами. Например, если n = 50, а m = 30, то при р = 0,1 для отыскания вероятности надо вычислить 50!, 30!, 20!, 0,1³⁰, 0,9²⁰. Но 50!=30 414 093 ∙ 10⁵⁷, 30! = 26 525 286 ∙ 10²⁵, 20!= 24 329 020 ∙ 10¹¹. Вычисления можно упростить, применяя таблицы логарифмов факториалов, но недостаток в этом случае состоит в том, что таблицы содержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности и в итоге окончательный результат может значительно отличаться от истинного.

Решить проблему позволяет локальная теорема Лапласа, которая даёт асимптотическую формулу, которая позволяет приближенно найти вероятность того, что событие в n опытах появиться m раз при условии, что вероятность появления события в каждом опыте одна и та же. Для частного случае при р=0,5 асимптотическая формула была найдена в 1730 году Муавром, а в 1783 году Лаплас обобщил формулу Муавра для произвольного значения р, отличного от 0 и 1.

Локальная теорема Муавра-Лапласа формулируется следующим образом:

Если вероятность p появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А в n опытах появится m раз выражается формулой

, (10.1)

где .

Формула (10.1) тем точнее, чем больше n.

Задачи.

1. Найти вероятность того, что при 100 выстрелах стрелок попадёт в мишень 75 раз при условии, что при одном выстреле он попадает в мишень с вероятностью 0,75.

2. Та же задача, только производится 10 выстрелов, ожидается 8 попаданий.

Решение.

1. ; ; ; . Формула Бернулли приводит к такому же результату.

2. , ;

. . Формула Бернулли приводит к иному результату, а именно . Столь значительное расхождение ответов объясняется тем, что в настоящем примере n имеет малое значение.

Если вероятность наступления события А близка к 0, а n – велико, то применение локальной формулы Муавра-Лапласа приводит к большой погрешности. В этом случае пользуются формулой Пуассона

,

где .

Задача. Вероятность изготовления нестандартной детали равна 0,004. Какова вероятность того, что из 1000 деталей 5 будут нестандартными?

Решение. .

11. Интегральная формула Муавра-Лапласа. Вероятность отклонения частоты события от его вероятности в n независимых испытаниях

Достаточно часто при решении задач требуется найти вероятность того, что некоторое событие произойдет число раз, заключенное в некоторых пределах. Рассмотрим пример такой задачи.

Задача. Вероятность поражения мишени стрелком при выстреле равна 0,75. Найти вероятность того, что при 4 выстрелах стрелок поразит мишень не менее 3 раз.

Решение. Найдем вероятности того, что стрелок при четырех выстрелах поразит мишень 0, 1, 2, 3 раза:

;

;

;

.

Вероятность того, что при 4 выстрелах стрелок поразит мишень не менее 3 раз выражается так: .

Искомую вероятность можно было найти по-другому:

.

В том случае, когда число испытаний достаточно велико для нахождения вероятности того, что некоторое событие произойдет число раз, заключенное в некоторых пределах, пользуются интегральной формулой Муавра-Лапласа:

Если вероятность p появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А в n опытах появится число раз, заключенное в пределах от a до b выражается формулой

, (11.1)

где , , 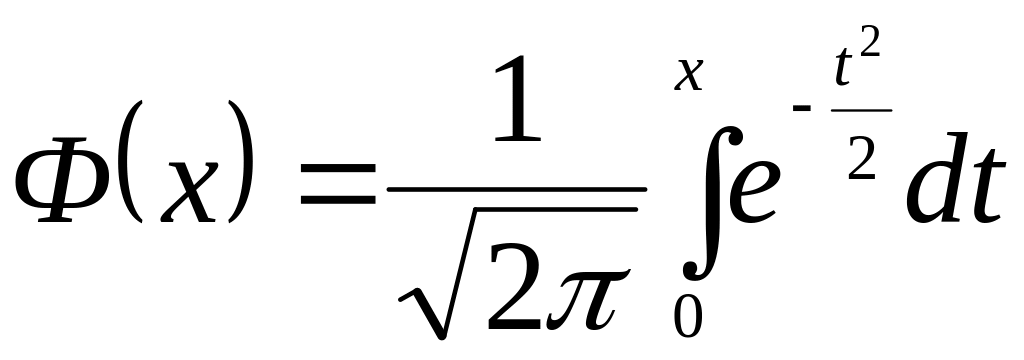- функция Лапласа.

Формула (11.1) тем точнее, чем больше n.

Замечания:

1. Табличные значения функции Лапласа приводятся в любых учебниках по теории вероятностей.

2. Ф(−х)=−Ф(х).

3. При х>5 Ф(х)=0,5.

Задача. Найти вероятность того, что из 1000 новорожденных мальчиков будет от 455 до 555 включительно, если вероятность рождения мальчиков равна 0,515.

Решение. В данной задaче a=455, b=555, p=0,515, q=0,485, n=1000.

Согласно интегральной формуле Муавра-Лапласа имеем:

В некоторых задачах придётся находить вероятность того, что число наступления события А будут заключено в границах: левая а меньше, а правая b больше числа np на одно и то же число r, т.е. a = np – r , b = np + r.

т.е.

(11.2)

В свою очередь из формулы (11.2) можно получить формулу для нахождения - вероятности того, что абсолютная величина отклонения частоты события А от вероятности этого события p в n независимых испытаниях не превзойдет данного положительного числа ε, если вероятность наступления события А в каждом испытании постоянна.

Для этого обе части неравенства умножим на n, получим: .

Таким образом, вероятность того, что абсолютная величина отклонения частоты события А от вероятности этого события p в n независимых испытаниях не превзойдет данного положительного числа ε, если вероятность наступления события А в каждом испытании постоянна выражается формулой

, (11.3)

где .

С помощью формулы (11.3) можно также находить и наименьшее число n испытаний, необходимых для того, чтобы с заданной вероятностью β отклонение частоты события А от вероятности его p по абсолютной величине не превзошла ε, если вероятность наступления события А в каждом испытании равна p.

Задача. Доля тяжёлых частиц в космическом излучении составляет в среднем 15%. Какое наименьшее число космических частиц должно быть зарегистрировано, чтобы с вероятностью 0,996 отклонение доли тяжёлых среди них от вероятности частицы быть тяжёлой не превзошло бы по абсолютной величине 0,04.

Решение. В данной задaче p=0,15, q=0,85, . Необходимо найти n. Имеем уравнение

,

или ,

или .

Решение последнего уравнения является n = 661. Это значит, что n = 661 – наименьшее число космических частиц должно быть зарегистрировано, чтобы с вероятностью 0,996 отклонение доли тяжёлых среди них от вероятности частицы быть тяжёлой не превзошло бы по абсолютной величине 0,04, т.е. будет заключено от 0,11 до 0,19.