Контрольные вопросы
Какое распределение вероятностей называется биномиальным распределением?
Какой смысл имеет с.в., распределенная по биномиальному закону с параметрами n и р?
Какое распределение вероятностей называется гипергеометрическим распределением?
Какими параметрами характеризуется гипергеометрическое распределение?
Какой смысл имеет с.в., распределенная по гипергеометрическому закону?
Какое распределение вероятностей называется геометрическим распределением? Чем объясняется такое название распределения?
Какой смысл имеет с.в., распределенная по геометрическому закону с параметром р?
Какое распределение вероятностей называется распределением Пуассона?
Почему закон распределения Пуассона также называют законом «редких событий»?
Как выглядят формулы для математического ожидания и дисперсии биномиального распределения?
Как выглядят формулы для математического ожидания и дисперсии геометрического распределения?
Как выглядят формулы для математического ожидания и дисперсии распределения Пуассона?
Контрольные задания
Доказать, что последовательность вероятностей, задаваемая формулой , где , k = 1, 2, …, n, … может задавать ряд распределения, т.е.
.Доказать, что математическое ожидание случайной величины, распределенной по геометрическому закону удовлетворяет формуле .
Доказать, что дисперсия случайной величины, распределенной по геометрическому закону удовлетворяет формуле .
Доказать, что последовательность вероятностей, задаваемая формулой Пуассона, может представлять собой ряд распределения, т.е. сумма вероятностей равна единице.
Доказать, что математическое ожидание случайной величины, распределенной по закону Пуассона удовлетворяет формуле М(Х)= =
.Доказать, что дисперсия случайной величины, распределенной по закону Пуассона удовлетворяет формуле D(Х)= .
Доказать, что сумма двух независимых случайных величин, распределенных по закону Пуассона с параметрами а и b является также случайной величины, распределенной по закону Пуассона с параметром а + b.
19. Типы распределений непрерывных случайных величин
19.1 Равномерное распределение
В некоторых задачах практики встречаются непрерывные величины, о которых заранее известно, что их возможные значения лежат в пределах определенного интервала [а; b]; кроме того, известно, что в пределах этого интервала [а; b] все значения случайной величины одинаково вероятны, т.е. обладают одной и той же вероятностью. В этом случае говорят, что случайная величина подчинена равномерному закону распределения, плотность вероятности такой случайной величины выражается формулой:
Для определения
плотности f(x)
воспользуемся свойством плотности
:
;
откуда
.
Плотность распределения f(x) имеет вид:
Данная формула и выражает закон равномерной плотности на интервале [а; b].
Функцию распределения F(x) найдем через интеграл от плотности распределения, несложно показать, что F(x) удовлетворяет выражению
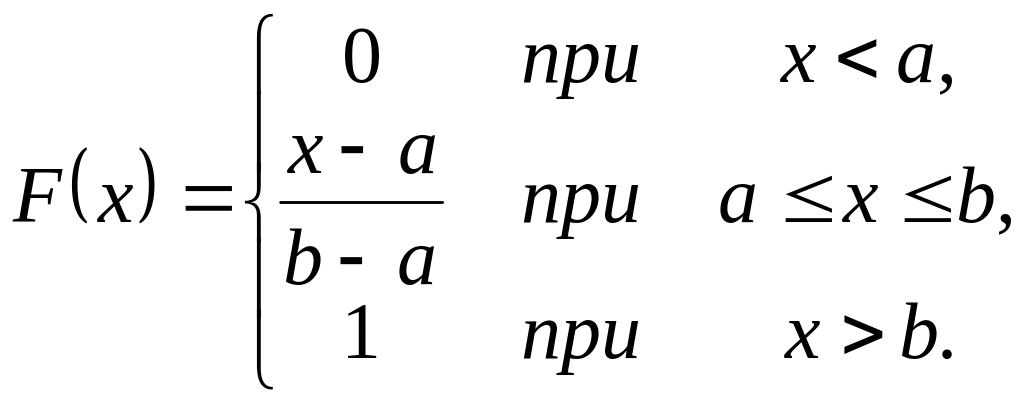
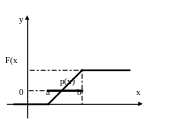
Определим основные числовые характеристики случайной величины Х, подчиненной закону равномерной плотности на интервале [а; b]:
;
;
.
Найдем вероятность попадания случайной величины Х, распределенной по закону равномерной плотности, на участок (α, β), представляющий собой часть участка [а; b]:
.
Равномерное распределение имеют, например, ошибки округления при проведении числовых расчетов. Такая ошибка, как правило, оказывается равномерно распределенной на интервале от – 5 до +5 единиц округляемого десятичного знака. Так, если вычисления проводятся с точностью до 0,001, то ошибка округления при этом равномерно распределена на отрезке [–0,005, 0,005].
Также равномерное распределение имеет время ожидания «обслуживания» при периодическом, через каждые Т единиц времени, включении (прибытии) «обслуживающего устройства» и при случайном поступлении (прибытии) заявки на обслуживание в этом интервале времени. Например, время ожидания пассажиром прибытия поезда метро при их точных пятиминутных интервалах движения и случайном моменте появления пассажира на платформе будет распределено равномерно на промежутке [0 мин, 5 мин].