19.2 Показательное распределение
В теории массового обслуживания, физике, биологии, в вопросах надежности имеем дело со случайными величинами, подчиненными показательному распределению:
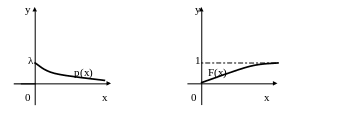
Найдем функцию распределения случайной величины Х, подчиненной показательному закону распределения:
.
Таким образом,
Вычислим основные числовые характеристики величины Х, подчиненной показательному распределению – математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача. Пусть случайная величина Х - время работы электрической лампочки – подчинена показательному распределению. Найти вероятность того, что время работы лампы меньше 600 часов, если в среднем лампа работает 400 часов.
Решение.
По условию задачи М(Х)=400,
значит λ=
.
Укажем две области применения теории вероятностей, где показательное распределение играет основную роль. К первой из них относятся задачи, связанные с величинами типа «времени жизни». Например, в медицине или биологии под ним может пониматься продолжительность жизни организмов; в психологии – время, затраченное испытуемым на выполнение тестовых заданий; в технике – время безотказной работы механизма.
Второй областью использования показательного распределения являются задачи массового обслуживания. Например, речь может идти о любой системе (телефонная станция, станция «Скорой помощи», билетная касса, ПЭВМ), предназначенной для обслуживания каких-либо требований или заявок, поступающих на нее в случайные моменты времени.
20. Нормальный закон распределения
Нормальный закон (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это наиболее часто встречающийся на практике закон распределения. Он является предельным законом, к которому приближаются другие законы распределения, поскольку можно доказать, что сумма достаточно большого числа независимых случайных величин, подчиненных каким угодно законам распределения приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется.
Нормальный закон распределения характеризуется плотностью вероятности вида:
.
Кривая распределения
носит название кривой Гаусса и представлена
выше. Кривая Гаусса имеет симметричный
холмообразный вид. Максимальная ордината
кривой, равная
,
соответствует точке х=m;
по мере удаления от точки m
плотность распределения падает, и при
кривая асимптотически приближается к
оси абсцисс.
Нормальный закон характеризуется двумя параметрами: m и σ. Выясним их вероятностный смысл. Для чего вычислим основные числовые характеристики величины Х – математическое ожидание и дисперсию:
то есть параметр m представляет собой математическое ожидание величины Х.
Следовательно, параметр σ в формуле есть среднее квадратическое отклонение величины Х.
21. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Правило трёх сигма
Найдем функцию распределения случайной величины Х, подчиненной нормальному закону распределения:
,
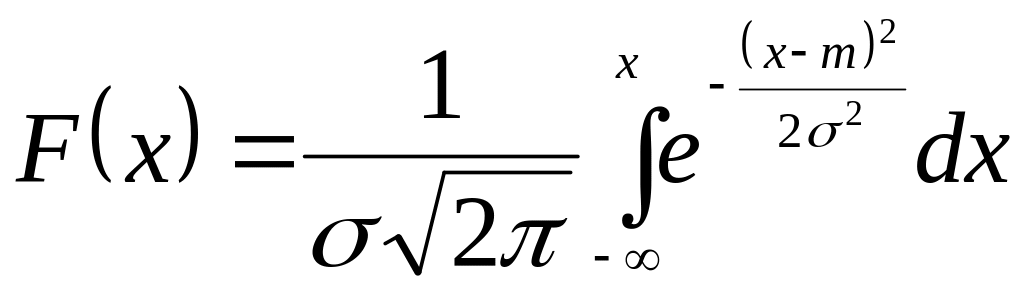сделаем в интеграле
замену
и приведем его к виду:
.
Интеграл
не выражается через элементарные
функции, но его можно вычислить через
специальную функцию, выражающую
определенный интеграл от выражения
или
.
Выразим функцию
через функцию Лапласа Ф(х):
.
Вероятность попадания случайной величины Х на участок (α, β) выражается формулой:
.
С помощью последней формулы можно оценить вероятность отклонения нормальной случайной величины от своего математического ожидания на заранее заданную сколь угодно малую положительную величину ε:
,
То есть
.
Пусть
,
тогда
и
.
При t=3
получим
,
т.е. событие, заключающееся в том, что
отклонение нормально распределенной
случайной величины от математического
ожидания, будет меньше
,
является практически достоверным.
В этом состоит правило трех сигм: если случайная величина распределена нормально, то абсолютная величина отклонения ее значений от математического ожидания не превосходит утроенного среднего квадратического отклонения.
Задача.
Пусть диаметр изготовляемой цехом
детали является случайной величиной,
распределенной нормально, m
= 4,5 см,
см.
Найти вероятность того, что размер
диаметра наудачу взятой детали отличается
от ее математического ожидания не более,
чем на 1 мм.
Решение.
Данная задача характеризуется следующими
значениями параметров, определяющих
искомую вероятность:
,
,
Ф(0,2)=0,0793,
