Контрольные вопросы

1. Какую случайную величину называют: а) двумерной; б) трехмерной; в) n-мерной?

2. Какая n-мерная случайная величина называется дискретной?

3. Как можно задать закон распределения двумерной дискретной случайной величины?

4. Как, зная закон распределения двумерной дискретной случайной величины, найти законы распределения ее составляющих?

24. Функция распределения двух случайных величин. Вероятность попадания случайной величины в полуполосу и прямоугольник

Ф ункцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств: X<x, Y<y:

.

Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения есть вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной в точке (х, у) (см. рисунок).

Свойства функции распределения системы случайных величин:

1. При любых значениях х и у , так как представляет собой вероятность.

2. есть неубывающая функция обоих своих аргументов, т.е. при х₂>x₁ , а при у₂>у₁ . В этом свойстве легко убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадания в квадрант с вершиной в точке (х, у). Действительно, увеличивая х (смещая правую границу квадранта вправо) или увеличивая у (смещая верхнюю границу вверх), мы не можем уменьшить вероятность попадания в этот квадрант.

3. Если хотя бы один из аргументов стремится к минус бесконечности, то , т.е. . В самом деле соответствующие вероятности как вероятности невозможных событий.

4. Если ровно один из аргументов стремится к плюс бесконечности, то функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу: т.е. , , где и - соответственно функции распределения случайных величин Х и У. В самом деле, вероятности и перестают зависеть от аргументов у и х соответственно.

5. Е сли оба аргумента равны плюс бесконечности, то функция распределения равна единице: . В самом деле, как вероятность достоверного события.

Вероятность попадания случайной точки в полубесконечную полосу, изображенную на рисунке слева .

Вероятность попадания случайной точки в полубесконечную полосу, изображенную на рисунке слева .

В ероятность попадания случайной точки в прямоугольник, изображенный на рисунке слева

25. Плотность распределения системы двух случайных величин. Законы распределения отдельных величин, входящих в систему

Функция распределения существует для любых систем случайных величин: непрерывных и дискретных. Наибольшее практическое значение имеют системы непрерывных случайных величин. Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.

Плотность распределения для одной случайной величины определялась как предел отношения вероятности попадания на малый участок к длине этого участка при ее неограниченном уменьшении. Аналогично определяется плотность распределения системы двух случайных величин.

Допустим, что система непрерывных случайных величин (X, Y) характеризуется функцией распределения , которая является непрерывной и дифференцируемой функцией. Функция р(x, y), задаваемая равенством

,

называется плотностью распределения системы.

Геометрически функцию можно изобразить некоторой поверхностью, которая называется поверхностью распределения.

Свойства плотности распределения:

1. р(x, у)0, т.е. является неотрицательной функцией, в с.д., F(x, у) – неубывающая функция;

2. Вероятность попадания случайной точки в произвольную область D выражается формулой ;

3. ;

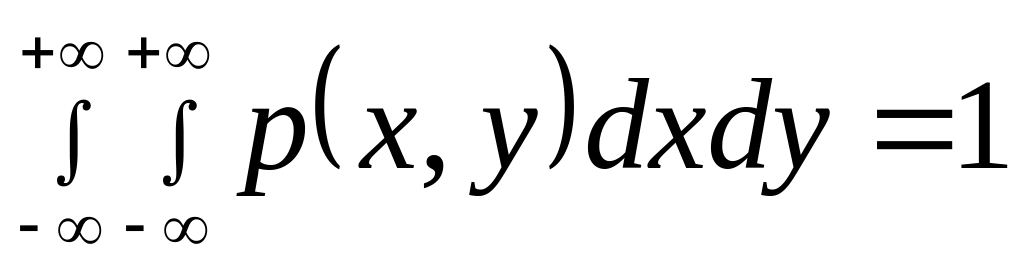4. . В с.д., указанный интеграл есть вероятность попадания случайной точки на всю плоскость хОу, т.е.вероятность достоверного события. Геометрически это свойство означает, что объем тела, ограниченного поверхностью распределения и плоскостью хОу, равен единице.

Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин. В частности, выше было показано, что выражения для функций распределения составляющих имеют вид:

, .

Выразим плотность распределения каждой из величин, входящих в систему, через плотность распределения системы. Для этого сначала выразим функции распределения составляющих системы через плотность распределения системы. В частности, для составляющей Х имеем:

.

Продифференцируем полученное равенство по х, получим выражение для плотности распределения составляющей х:

.

Аналогично

.

Таким образом, для того чтобы получить плотность распределения одной из величин, входящих в систему, нужно плотность распределения системы проинтегрировать в бесконечных пределах по аргументу, соответствующему другой составляющей.