§6. Распределение Максвелла.

В газе, находящимся в равновесии при температуре Т, скорость каждой отдельно взятой молекулы из-за столкновений непрерывно изменяется как по своему значению, так и по направлению. Поскольку в состоянии равновесия все направления движения молекул газа равновероятны, то распределения молекул по направлениям движения равномерно.

Иначе обстоит дело с абсолютными значениями скоростей молекул: они не будут равновероятны. Однако установившееся распределение молекул по значениям скорости не нарушается вследствие молекулярного движения и столкновений, т.е. оно не зависит от времени. Это значит, что непрерывное перераспределение скоростей между молекулами происходит так, что число молекул, обладающих значениями скорости, заключёнными в любом интервале [υ₁, υ₂], все время остается постоянным. И это подтверждает опыт.

Пусть газ находится в равновесии при температуре Т и имеет N молекул массы m₀ каждая. Тогда число молекул dN_, скорости которых имеют значения от υ до υ+dυ (т.е. заключены внутри интервала dυ, лежащего возле точки υ), очевидно, пропорционально общему числу молекул N в газе, величине интервала d, а также будет зависеть от самого значения скорости υ (последнее следует из неравномерного распределения абсолютных значений скорости), т. е.

(64)

dN_=NF(υ)dυ

где F(υ) ― функция, характеризующая распределение молекул по скоростям.

Равенство (64) можно переписать в виде:

(65)

В левой части равенства (65) стоит величина равная вероятности того, что «взятая наугад» молекула будет иметь скорость заключенную в интервале [υ, υ+dυ] (см. приложение А)

(66)

Если проинтегрировать (66) по всем возможным скоростям (значения скоростей будем предполагать изменяющиеся от 0 до ∞), то получим, согласно условию нормировки вероятности (см. приложение А),

(67)

,

которое физически означает, что «взятая наугад» молекула имеет какую-то скорость с вероятностью равной единице, т.е. достоверно.

Из (67) и (66) следует, что

(68)

Можно показать, что функция распределения по скоростям F(V) имеет вид:

(69)

Функцию F(υ) называют распределением Максвелла по абсолютным значениям скоростей молекул.

§7. Свойства распределения Максвелла.

На рис.4 представлен график функции F(υ). Как видно из рисунка, функция F(υ) имеет асимметричный вид относительно её максимальной ординаты.

Вероятность того, что величина скорости молекулы заключена в приделах от υ₁, до υ₂ (см. приложение А)

(70)

и изображается горизонтально заштрихованной площадью. Вероятность того, что скорость молекула превышает некоторое значение υ₀,

(71)

и на графике изображается вертикально заштрихованной площадью. Вся площадь под кривой и осью υ равна единице. Это следует из соотношения (68). Из графика F(υ) также видно, что доля молекул в газе, обладающих малыми скоростями, так же как и доля молекул, обладающая очень большими скоростями мала. Наибольшая часть молекул обладает скоростями, близкими к скорости, соответствующей максимуму функции F(υ). Эта скорость υ_В называется наиболее вероятной. Дифференцируя (69) по υ и приравнивая полученное выражение к нулю, находим выражение для вероятной скорости.

(72)

Подставляя это значение скорости в (69), находим значение максимальной ординаты функции F(υ)

(73)

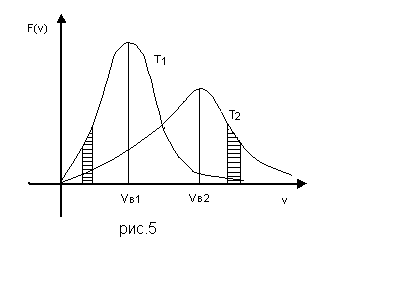
Из (72) и (73) следует, что при увеличении температуры максимум кривой F(υ) смещается в сторону больших скоростей и становится ниже, причём площадь под кривой остаётся неизменной и равной единице. Кривые распределения молекул одного и того же газа по скоростям при различных температурах имеют, поэтому вид, представленный на рис.5 (Т₁<Т₂).

Из рис.5 видно, чем больше температура газа, тем выше идёт правая ветвь кривой и тем ниже опускается её левая ветвь. Это означает, что с повышением температуры увеличивается доля молекул с большими скоростями и уменьшается доля молекул с малыми скоростями.

И з формулы (69) для функции F(υ), а также (72) и (73) видно, что F(υ) зависит также от природы газа, т.е. от массы его молекул m₀. Для разных газов при одной и той же температуре кривая распределения оказывается различной, причем, чем больше масса молекул, тем υ_в меньше, а F_max больше и, следовательно, тем более крутой имеет вид кривая F(υ). Кривая F(υ), соответствующая одной и той же температуре Т, но разным массам молекул m₀₁ и m₀₂ (m₀₁ > m₀₂) приведены на рис.6. Как видно, при одной и той же температуре у тяжёлого газа малые скорости встречаются чаще, а большие ― реже, чем у газа, состоящего из лёгких молекул.

Зная функцию F(υ), можно вычислить важные для молекулярной физики величины: среднюю скорость и среднюю квадратичную скорость молекул газа. Согласно формулам вычисления средних (см. приложение А)

(74)

(75 )

Подставляя в формулы (74) и (75) функцию распределения F(υ), получим после интегрирования

(76)

(77)

Из выражений (76) и (77) видно, что средняя квадратичная и средняя скорости молекул возрастают с ростом температуры. Это возрастание пропорционально квадратному корню из абсолютной температуры. Кроме того, эти скорости обратно пропорциональны корню квадратному из массы молекул.

Из сравнения формул (72), (76) и (77) заключаем, что наименьшей из трёх характерных скоростей максвелловского распределения является наиболее вероятная, а наибольшей ― средняя квадратичная, т. е.

(78)