4.11Критерии оптимальности
Для того чтобы точка выпуклого множества являлась точкой минимума выпуклой и дифференцируемой на функции , т.е. оптимальной, необходимо и достаточно, чтобы для любого выполнялось (99).
Следствие. Если функция строго выпукла, то единственна.
Доказать самостоятельно.
Итак, изучая выпуклые функции и их связь с выпуклыми множествами мы увидели важнейшее свойство этих объектов: если для выпуклой функции существует точка локального экстремума на выпуклом замкнутом множестве, то она является и точкой глобального экстремума; для строго выпуклой функции эта точка является единственной.
Введем вектор
=
—
,
где
— любое число. Пусть
=
.
Для того чтобы точка выпуклого множества являлась точкой минимума выпуклой и дифференцируемой на функции , необходимо и достаточно, чтобы =
,
где
=
—
.
Доказать самостоятельно.
Если от не требовать условия выпуклости, то справедливо следующее утверждение:
для
того чтобы точка
выпуклого множества
являлась точкой локального минимума
дифференцируемой на
функции
,
необходимо и достаточно, чтобы
=
=
.
Будет ли функция
=
выпукла на множестве
={
}?
При каких действительных значениях параметра выпукло множество
={
}?
Построить гиперплоскость, разделяющую множества
={
}
и
={
}.
Лекция № 5.Основы выпуклого программирования. Теория Куна-Таккера
Содержание учебного плана: задача выпуклого программирования (ЗВП) как задача определения стратегий-констант на выпуклом множестве контролируемых факторов; множители Лагранжа и их интерпретация; функция Лагранжа; условия регулярности; седловые точки и достаточные условия оптимальности ЗВП; теорема Куна-Таккера; дифференциальные условия Куна-Таккера.
Изучая операции, в которых отсутствуют неуправляемые факторы, приходим к необходимости решения задачи математического программирования:
.
Оптимизация
на множестве стратегий-констант
,
может пониматься как максимизация
показателя эффективности
,
так и его минимизация.
5.1Основная задача выпуклого программирования
Пусть задано выпуклое
и замкнутое множество
.
Рассмотрим множество
={
},
=(
,…,
),
.
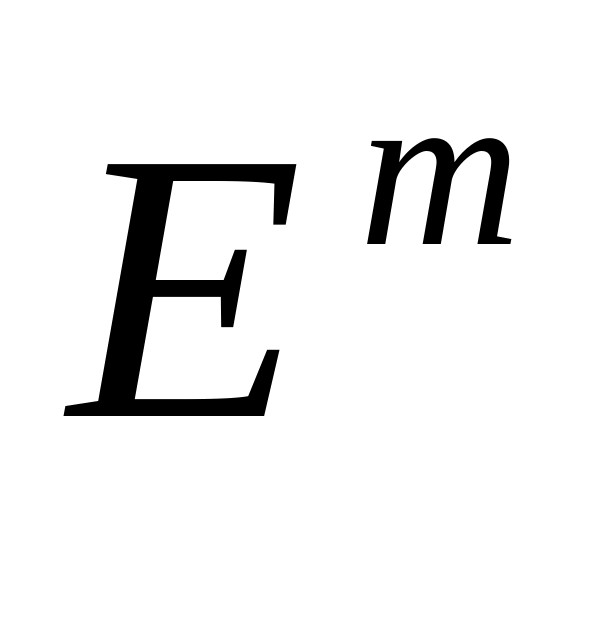где
(
)
— вогнутые (выпуклые вверх) непрерывные
на
скалярные функции. В теории математического
программирования каждый элемент
принято называть допустимым планом,
а само множество
— множеством допустимых планов.
Доказать самостоятельно выпуклость множества .
5.2Формальная постановка задачи выпуклого программирования
Задачу
,
где
выпукла, а
определяется условиями (101), называется
основной задачей выпуклого программирования.
Определение 31. означает, что ставится задача:
Если существует минимальное значение функции на множестве , то среди всех допустимых планов найти оптимальный план , для которого
=
=
при этом число называют значением задачи.
Если оптимального плана не существует, то требуется
а) либо найти значение задачи как точную нижнюю грань значений функции на множестве :
=
б) либо убедиться, что неограничена снизу на множестве ;
в) либо убедиться в том, что множество допустимых планов пусто.