4.2Определение и примеры выпуклых множеств.
Множество называют выпуклым, если вместе с любыми двумя точками , ему принадлежит и соединяющий их отрезок [ , ].
Выпуклость множества
означает, что для всех
,
и любого действительного числа
вектор
=(
+(1—
)
)
.
Уважаемые коллеги! Прошу Вас доказать выпуклость самостоятельно!
-Мерный куб с центром в точке и ребром :
=
.
-Мерный шар радиуса с центром в точке :
Гиперплоскость в , т.е. множество
,
где
— ненулевой вектор, называемый нормалью
к гиперплоскости,
.
В пространстве гиперплоскость определяет два полупространства:
и
.
Множество решений системы линейных равенств и неравенств:
,
где , — произвольные матрицы, выпукло и замкнуто.
Пусть вектор
.
Множество
называется стандартным симплексом и является выпуклым множеством.
Если выпукло, то выпуклы внутренность и замыкание .
Если , а точка , то полуинтервал [ , ) .
На каждом луче, исходящем из произвольной внутренней точки выпуклого множества , имеется самое большее одна граничная точка.
Привести пример множества , которое вместе с любыми своими точками , содержит точку
=(
+
)/2
и в то же время не является выпуклым
(необходима замкнутость).
Сумма конечного числа выпуклых множеств выпукла.
Пересечение конечного числа выпуклых множеств выпукло.
ДОКАЗАТЕЛЬСТВО следует непосредственно из определения выпуклого множества.
4.3Проекция точки на множество. Свойства.
Для заданной точки
определим число
и множество
,
=
.
Число
называют расстоянием точки
до множества
.
Проекцией
точки
на выпуклое множество
называют такую точку
,
что:
= ,
Для любого выпуклого замкнутого множества и любой точки существует единственная точка , являющаяся проекцией на .
ДОКАЗАТЕЛЬСТВО.
1. Существование
проекции следует из замкнутости множества
.
Действительно, если
,
то очевидно, что
=
и
.
Пусть точка
.
По определению числа
как точной нижней грани существует
такая последовательность {
}
точек
,
что
,
т.е. последовательность {
}
ограничена. В силу ограниченности
последовательности {
}
по тероеме Вейерштрасса найдется ее
сходящаяся подпоследовательность {
},
т.е.
.
Поскольку
замкнуто, то
.
2. Для доказательства
единственности предположим, что
существуют такие точки
,
,
,
что
и
Поскольку множество выпукло, то точка =( + )/2 принадлежит ; но из неравенства треугольника 3.3 (теоремы Пифагора) следует:
,
что противоречит либо определению , либо условию .
Для того чтобы точка была проекцией точки на выпуклое замкнутое множество , необходимо и достаточно, чтобы для всех выполнялось неравенство:
.
ДОКАЗАТЕЛЬСТВО. 1)
Пусть
=
и
.
Рассмотрим
.
Ввиду выпуклости
для любого
.
Так как
.
По определению для любого
.
Следовательно, для
любого
,
откуда следует (81).
2) Пусть теперь справедливо (81). Тогда для любого будет
.
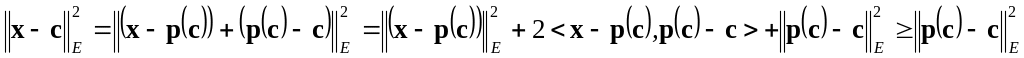т.е. = .
Для любого
.
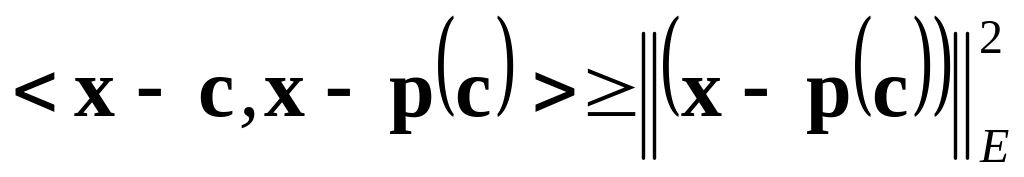и
.
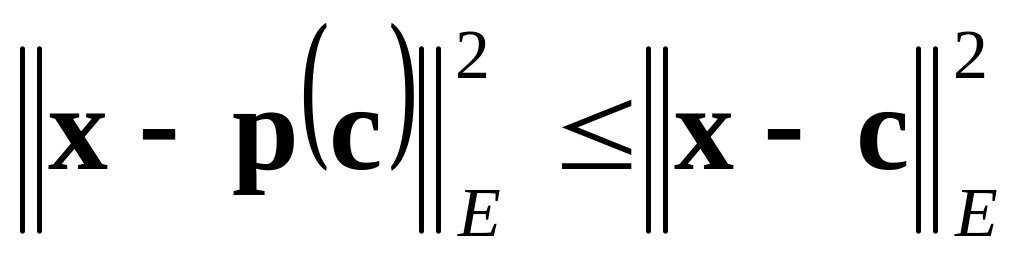Доказать самостоятельно. Дать геометрическую интерпретацию соотношений (86) и (87).