3.8Линейная обработка измерений (фильтрация) координат движущихся объектов

Эта задача лежит в основе теории автоматического регулирования.

Рассмотрим движение объекта, характеризуемое одной координатой , которую будем рассматривать в дискретные моменты времени и соответственно обозначать .

В результате измерений оперирующей стороне будет известно не , а величины + , где — случайные ошибки измерения. Для увеличения точности знания предлагается использовать линейную фильтрацию измерений путем введения в качестве приближенных значений величин величины

69. ,

где — весовые коэффициенты фильтрации ( не обязательно положительные). Здесь отражает априорное (до измерений) представление о величине .

В качестве ошибки фильтрации принимают критерий

70. = ,

При решении задачи фильтрации обычно разрешено осреднение критерия (70) по случайностям, при этом считаются независимыми со стандартными нормальными законами распределения (отсутствует систематическая ошибка измерения). Тогда выражение критерия эффективности приобретает вид

71. = ,

где дисперсия . Стратегиями оперирующей стороны здесь является выбор величин . Этот выбор, естественно, зависит от величины , которая, вообще говоря, является первым неопределенным фактором, хотя может быть и фиксирована. Это типичная природная неопределенность. Вторым неконтролируемым фактором является закон изменения . Как в предыдущем случае, здесь может быть много осмысленных вариантов.

3.8.1Случайное блуждание координат движущегося объекта

В этом случае предполагается, что случайны с равным нулю (или, что все равно, постоянным) математическим ожиданием, с известными дисперсиями и корреляцией между для разных . Эту постановку задачи изучали Колмогоров и Винер. Простейшими случаями здесь являются: все одинаковы (полная зависимость), и полная отсутствие корреляции.

3.8.2Зависимое блуждание координат движущегося объекта

В этом случае предполагается, что зависимость от принадлежит определенному классу функций, зависящих от параметров , значения которых неизвестны. В постановке задачи Рагозина и Заде

72. .

Эта задача имеет решение лишь в случае

73. ; .

Задача сводится к минимизации

74. = ,

при условиях (72)-(73).

Простейшими случаями здесь являются: все одинаковы (полная зависимость), и полная отсутствие корреляции.

3.8.3Ограниченное блуждание координат движущегося объекта

описывают движение объекта с ограниченными возможностями. Тогда неопределенные факторы подчинены условиям

75. .

Лекция № 4.Элементы выпуклого анализа

Содержание учебного плана: евклидово пространство; неравенство Коши-Буняковского; топологические, метрические и нормированные пространства в евклидовом пространстве; примеры выпуклых множеств; свойства выпуклых множеств и теорема о разделяющей гиперплоскости; крайние точки выпуклого множества; теорема о представлении произвольной точки выпуклого множества выпуклой комбинацией его крайних точек; выпуклые функции и их свойства; связь между выпуклыми функциями и выпуклыми множествами (4 ч.).

Мы будем, как правило, рассматривать функции, определенные на подмножествах конечномерного евклидова пространства .

4.1Вспомним основные понятия высшей алгебры

Напомним, что евклидово пространство является:

1. линейным пространством над множеством , т.е. множеством -мерных вещественных векторов, на элементах которого определены операции сложения и умножения со следующими свойствами:

   1. каждой паре векторов ,  (элементов нашего множества) отвечает вектор + , называемый суммой векторов и , при этом сложение

      1. коммутативно: + = + ;

      2. ассоциативно: +( + )=( + )+ ;

      3. существует нулевой вектор 0 такой, что +0= для любого вектора  ;

      4. для каждого вектора существует обратный элемент такой, что + =0.

   2. каждой паре ( , )  отвечает вектор , называемый произведением числа на вектор , при этом произведение

      1. ассоциативно: для любых чисел , и любого вектора =

      2. = для любого вектора .

   3. Операции сложения и умножения связаны между собой соотношениями

      1. умножение на число дистрибутивно относительно сложения векторов, т.е.

( + )= + ,

2. умножение на вектор дистрибутивно относительно сложения чисел,

( + ) = + .

Свойства 1.1 описывают множество векторов с точки зрения операции сложения и говорят о том, что оно по отношению к этой операции является абелевой группой.

Свойства 1.2 описывают множество векторов с точки зрения операции умножения вектора на число.

Свойства 1.3 описывают связь двух операций между собой.

2. Каждой паре векторов ,  соответствует число, < , >, называемое скалярные произведением, удовлетворяющее следующим свойствам:

   1. < , >=< , >;

   2. < , >= < , >;

   3. < + , >=< , >+< , > для любых , ,  ;

   4. < , >=0 при =0, <0,0>=0.

Вектор  называется нормированным, если < , >=1.

Скалярное произведение обладает важным свойством, известным как неравенство Коши-Буняковского:

для любых двух векторов ,  справедливо неравенство:

76. (< , >)²(< , >)*(< , >).

9. Неравенство Коши-Буняковского обращается в равенство тогда и только тогда, когда векторы ,  коллинеарны.

3. Евклидово пространство является нормированным, поскольку в нем введено понятие евклидовой нормы вектора :

,

для которой справедливы следующие соотношения:

1. , причем тогда и только тогда, когда =0;

2. = ;

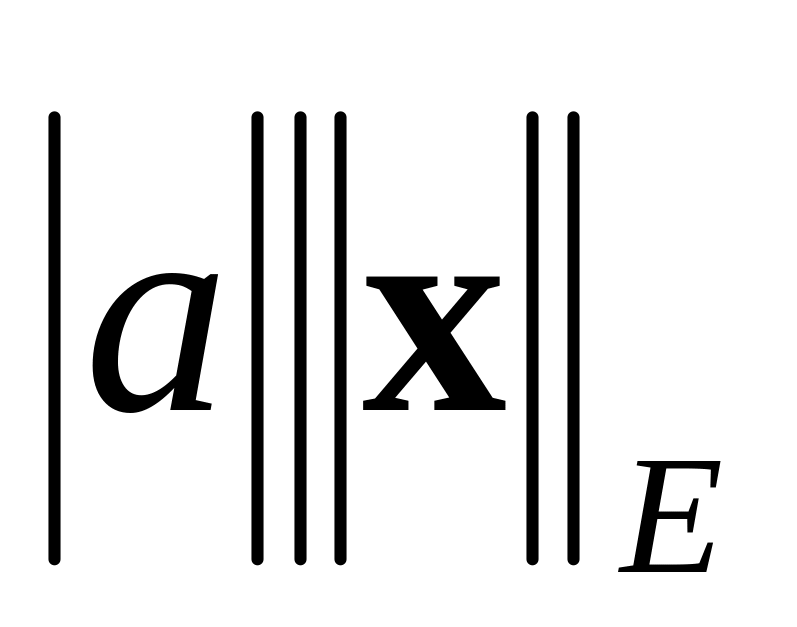3. — неравенство треугольника.

Евклидова норма и скалярное произведение связаны неравенством Коши-Буняковского:

77. (< , >)² .

Евклидова норма порождает в сходимость по норме.

Будем говорить, что последовательность { } точек  сходится к точке  при , т.е. , если .

Множество будем называть -окрестностью точки .

Множество называют замкнутым, если оно содержит все свои предельные точки, т.е. такие точки, что любой окрестности каждой из них принадлежит бесконечно много точек из . Замкнутое ограниченное множество называется компактом в .

Точка  называется внутренней точкой множества , если существует такая ее -окрестность, все точки которой принадлежат множеству . Множество всех внутренних точек множества называется внутренностью .

Точка  называется граничной точкой множества , если любая ее -окрестность содержит как точки, принадлежащие , так и точки, ему не принадлежащие. Множество, состоящее из всех граничных точек множества , называется границей множества .

Множество с его границей называется замыканием множества и обозначается .

10. Доказать, что множество граничных точек компакта непусто.

Суммой двух множеств ,  называют множество

={ : = + ,  ,  },

состоящее из всех попарных сумм элементов множеств , .