94. 6. Деякі властивості функцій

Однією з основних задач математичного аналізу є визначення властивостей функції.

Функція , що має область визначення симетричну відносно початку координат, називається парною, якщо :

і непарною, якщо :

.

Прикладами парних функцій можуть бути функції , і т.д. Відповідно непарними функціями є функції , .

Відзначимо, що функція може бути ні парною, ні непарною, наприклад, , , та ін.

Неважко показати, що графіки парних функцій симетричні відносно вісі ординат, а графіки непарних функцій симетричні відносно початку координат.

Функція називається періодичною, якщо існує таке додатне число : . При цьому число називається періодом функції. Відомо, що функції , періодичні з періодом , а функції , періодичні з періодом .

Можна показати, якщо число є періодом функції, число ( ) також є періодом цієї функції. Якщо функція періодична з періодом , функція періодична з періодом . Справді, . Наприклад, функція періодична з періодом , функція періодична з періодом .

Нулями функції називаються абсциси точок перетину графіка функції з віссю абсцис, тобто розв’язки рівняння . Розв’язати рівняння іноді важко, що вимагає наближених методів.

Функція називається зростаючою на проміжку, якщо для будь-яких значень аргументів цього проміжку з умови випливає, що , тобто більшому значенню аргументу відповідає більше значення функції.

Відповідно функція називається спадною на проміжку, якщо для будь-яких двох значень цього проміжку з умови випливає, що , тобто більшому значенню аргументу відповідає менше значення функції.

Функція називається не зростаючою на проміжку, якщо для будь-яких значень аргументів цього проміжку з умови випливає, що .

Відповідно функція називається не спадною на проміжку, якщо для будь-яких двох значень цього проміжку з умови випливає, що .

Зростаючі, спадні, не зростаючі та не спадні функції називаються монотонними.

95. 7. Функція, обернена до даної

Нехай функція визначена і монотонна в деякій області. Задаючи значення , будемо одержувати відповідні значення . Можна, вважаючи аргументом, а функцією, задавати значення і обчислювати відповідні значення . У такому випадку рівняння буде визначати як неявну функцію від .

Припустимо, що задане рівняння розв’язане відносно , тобто, одержимо . Знайдена функція називається оберненою до функції .

Якщо, дотримуючись стандартних позначень, під розуміти незалежну змінну, а під – функцію, тобто залежну змінну, обернену функцію варто писати у вигляді .

Функції і задають тим самим графіком, оскільки визначають ту саму функціональну залежність між x і y.

Рис. 2.2.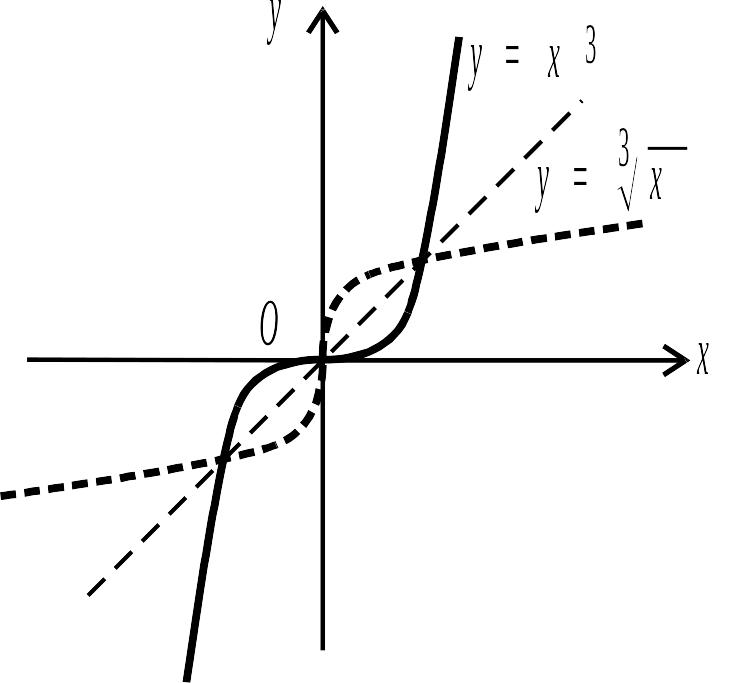

Якщо ж умовитися позначати незалежну змінну через , а залежну через , то, щоб із графіка даної функції одержати графік оберненої їй функції , досить перший графік дзеркально відобразити відносно прямої .

Так, щоб знайти функцію обернену до , знайдемо і перемінимо місцями і , одержимо функцію , обернену до функції , графік якої зображено на рис. 2.2.