141. 8. Неявно задані функції

Означення 4.14. Якщо змінна , яка є функцією аргументів задається за допомогою рівняння , то говорять, що функція задана неявно.

Наприклад, .

Розглянемо функцію , задану рівнянням

(4.10)

Продиференцюємо рівняння (4.10) по змінній та :

,

З останніх рівностей одержимо формули:

, .

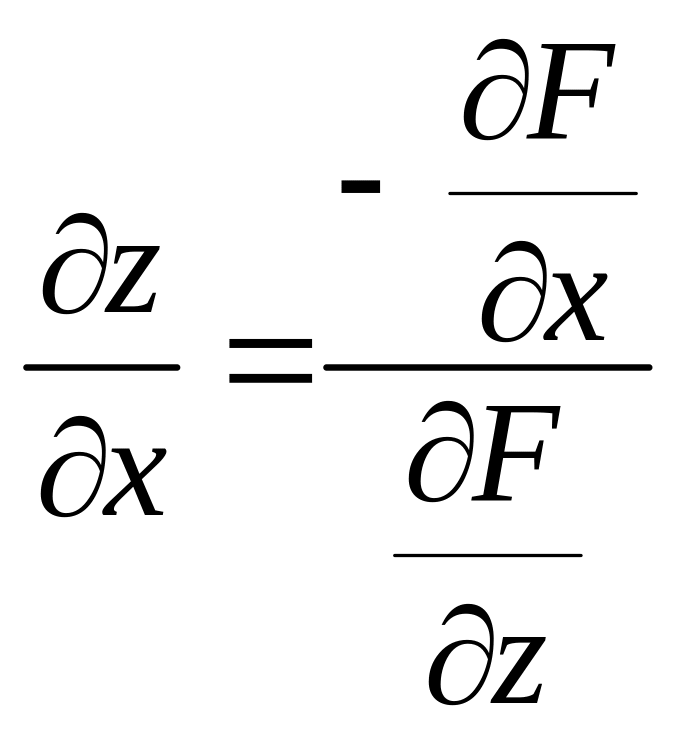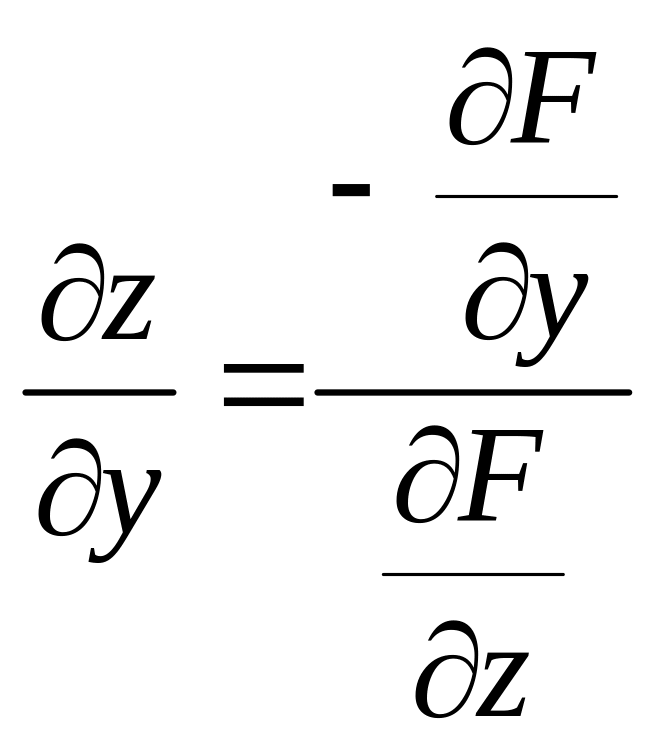Аналогічно можна ввести поняття частинних похідних другого, третього, будь-якого порядку.

Іноді неявні функції визначають системою функціональних рівнянь. Нехай функції знаходять як розв’язки системи рівнянь:

(4.11)

Розглянемо визначник:

.

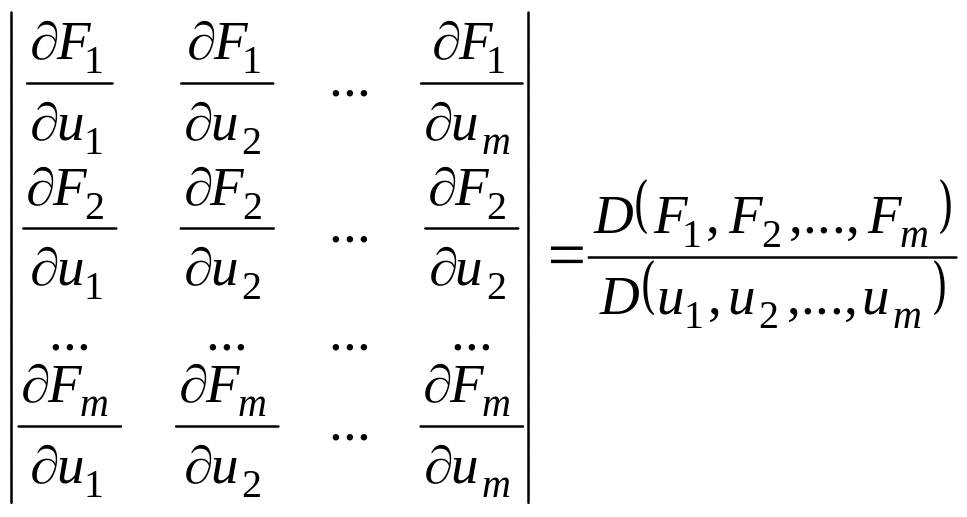Цей визначник називають визначником Якобі або якобіаном функцій по змінним .

Продиференцюємо рівняння системи (4.11) по змінній :

Цю систему можна розв’язати відносно змінних , ..., по формулам Крамера. Одержимо формули для знаходження частинних похідних:

.

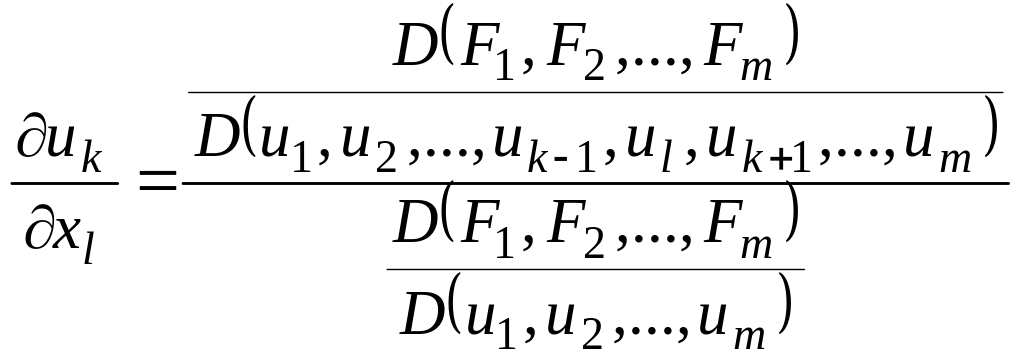142. 9. Умовний екстремум

Розглянемо функцію

. (4.12)

Нехай виконуються умови:

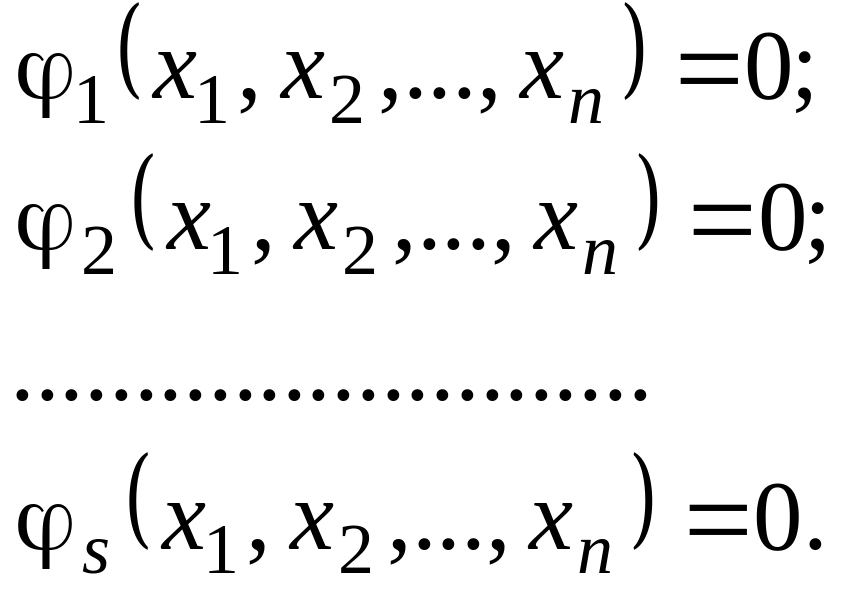(4.13)

Дослідження функції (4.12) на екстремум при виконанні умов (4.13) називають задачею на умовний екстремум.

Існує декілька шляхів розв’язання цієї задачі. Розглянемо метод Лагранжа.

Побудуємо допоміжну функцію

,

де – поки що невідомі множники Лагранжа. Будемо досліджувати побудовану функцію на локальний екстремум.

Приклад 4.7. Знайти умовний екстремум функції при умові: .

Розв’язання. Побудуємо функцію Лагранжа:

.

Дослідимо цю функцію на екстремум. Запишемо необхідну умову екстремуму та знайдемо стаціонарні точки з системи:

Стаціонарними точками будуть: при , при . Знайдемо другий диференціал в стаціонарних точках за формулою: . Для точки : .

Знак другого диференціалу невизначений, тобто в цій точці немає ні максимуму ні мінімуму.

Для точки : .

Оскільки , то . Тоді одержимо:

, тобто в цій точці максимум.

143. 10. Найбільше і найменше значення функції в області

Якщо функція визначена і неперервна в замкнутій обмеженій області , то вона набуває в цій області свого найбільшого і найменшого значень.

Для знаходження найбільшого і найменшого значень функції в області потрібно знайти всі критичні точки всередині області, обчислити значення функції в цих точках, потім знайти найбільше і найменше значення функції на границі області і з усіх отриманих таким чином значень вибрати найбільше і найменше.

Приклад 4.8. Знайти найбільше і найменше значення функції в замкнутій області, обмеженої лініями , , (рис.4.5).

Рис. 4.5.

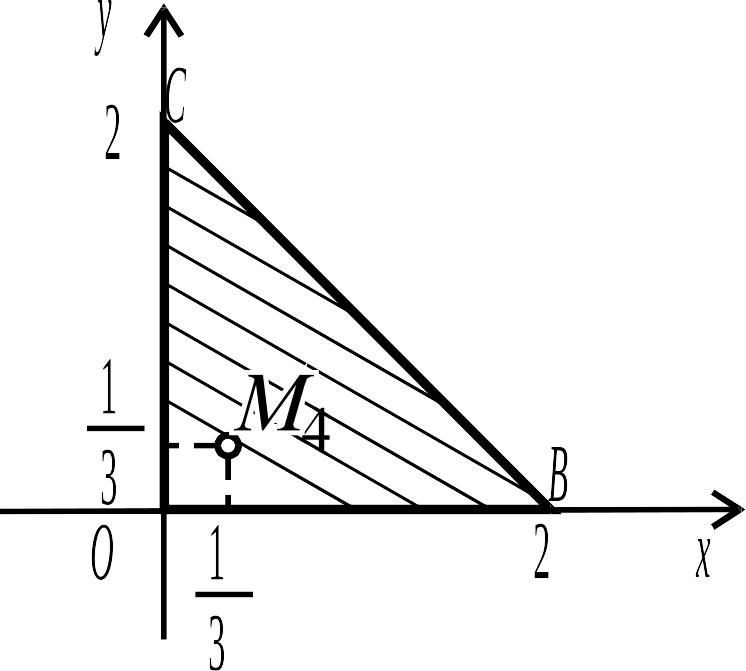
Розв’язання. Досліджуючи цю функцію на екстремум знайдемо чотири критичні точки , , , , з яких лише одна точка лежить всередині даної області. Значення функції в цій точці . Дослідимо функцію на границі області.

На маємо , . На маємо x=0, . На маємо і функція набуває вигляду причому . Похідна цієї функції при . Значення функції в цій точці .

На границях відрізка у точках і значення функції .

Порівнюючи знайдені значення, дійдемо висновку, що найбільше значення функції в даній області досягається всередині області в точці , тут . Найменшого значення функція набуває на межі області у точці , тут .