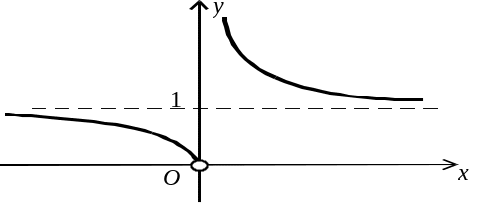- •Розділ 1. Теорія множин
- •1. Поняття множини
- •2. Найпростіші операції над множинами
- •3. Числові множини
- •4. Обмежені множини. Верхні та нижні грані множин
- •5. Поняття функції (відображення)
- •6. Еквівалентні множини. Потужність множин
- •7. Потужність континуума
- •Розділ 2. Послідовності. Функції однієї змінної
- •1. Числові послідовності
- •2. Границя послідовності
- •3. Застосування послідовностей в економіці
- •4. Поняття функції
- •5. Способи задання функції
- •6. Деякі властивості функцій
- •7. Функція, обернена до даної
- •8. Класифікація функцій
- •9. Основні методи побудови графіків функцій
- •10. Приклади застосування функцій в економіці
- •11. Границя функції
- •12. Нескінченно малі і нескінченно великі функції
- •13. Основні теореми про границі функцій
- •14. Обчислення границь функцій
- •15. Істотні границі Перша істотна границя
- •Друга істотна границя
- •16. Порівняння нескінченно малих
- •17. Неперервність функції в точці
- •18. Властивості функцій, неперервних в точці
- •19. Точки розриву і їхня класифікація
- •20. Властивості функцій, неперервних на відрізку
- •Розділ 3. Диференціальне числення функції однієї змінної
- •1. Задачі, що приводять до поняття похідної функції
- •2. Поняття похідної
- •3. Геометричний зміст похідної. Рівняння дотичної і нормалі до кривої
- •4. Диференційованість функції в точці
- •5. Похідні елементарних функцій
- •6. Основні правила диференціювання
- •7. Похідна складної функції
- •8. Логарифмічне диференціювання. Похідна степеневої, показникової, показниково-степеневої функцій
- •9. Похідна оберненої функції. Похідні обернених тригонометричних функцій
- •10. Таблиця похідних
- •11. Похідна неявно заданої функції
- •12. Похідна функції, заданої параметрично
- •13. Похідні вищих порядків
- •14. Наближені обчислення за допомогою похідної
- •15. Еластичність функції
- •Еластичності елементарних функцій:
- •16. Застосування еластичності в економічному аналізі Еластичність попиту відносно ціни
- •Еластичність і податкова політика
- •17. Основні теореми диференціального числення
- •18. Правило Лопіталя
- •19. Зростання і спадання функції на проміжку
- •20. Екстремуми функції
- •Необхідна умова екстремуму диференційованої функції.
- •Перша достатня умова екстремуму.
- •Друга достатня умова екстремуму.
- •Третя достатня умова екстремуму.
- •21. Найбільше і найменше значення функції на відрізку
- •22. Випуклість, увігнутість графіка функції. Перегин
- •Необхідна і достатня умова випуклості (увігнутості) графіка функції.
- •Необхідна умова точки перегину.
- •Достатні умови точки перегину.
- •23. Асимптоти графіка функції
- •24. Повне дослідження і побудова графіка функції
- •25. Застосування похідної в економіці Граничний аналіз в економіці.
- •Задачі на екстремум.
- •Розділ 4. Диференціальне числення функції багатьох змінних
- •1. Основні поняття
- •2. Границя і неперервність
- •3. Частинні похідні функції
- •4. Повний диференціал
- •5. Похідна функції за даним напрямком. Градієнт
- •6. Частинні похідні і диференціали вищих порядків
- •7. Локальний екстремум функції багатьох змінних
- •8. Неявно задані функції
- •9. Умовний екстремум
- •10. Найбільше і найменше значення функції в області
- •11. Метод найменших квадратів
- •12. Економічні задачі
18. Властивості функцій, неперервних в точці
Теорема 2.7. Сума, різниця, добуток скінченного числа функцій, неперервних у точці x0, також неперервні в цій точці.
Теорема 2.8. Частка від ділення двох функцій, неперервних у деякій точці x0, також неперервна в цій точці за умови, що знаменник у цій точці не дорівнює нулю.
Теореми доводяться на підставі відповідних теорем про границі.
Доведемо, наприклад, теорему 2.8. Нехай
функції
і
неперервні в точці
і
![]() .
Це значить, що
,
.
Це значить, що
,
![]() .
.
Розглянемо функцію
![]() .
Для цієї функції:
.
Для цієї функції:
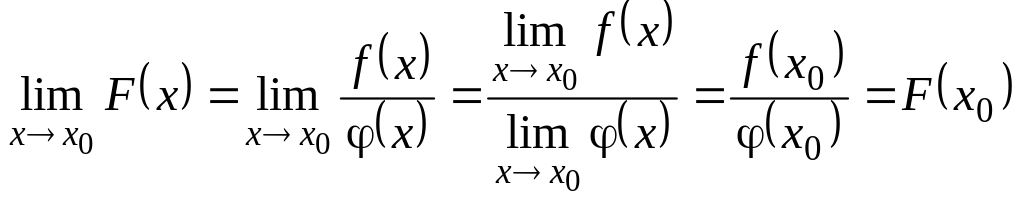 ,
,
тобто функція
![]() неперервна в точці
.
неперервна в точці
.
Теорема
2.9. Якщо функція
неперервна в точці
![]() ,
а функція
неперервна в точці
,
причому
,
а функція
неперервна в точці
,
причому
![]() ,
то складна функція
неперервна в точці
.
,
то складна функція
неперервна в точці
.
Покажемо, що для складної функції
виконується означення неперервності:
![]() ,
тобто складна функція
,
тобто складна функція
![]() неперервна в точці
.
неперервна в точці
.
На підставі приведених теорем можна стверджувати, що всяка елементарна функція неперервна в кожній точці своєї області визначення.
19. Точки розриву і їхня класифікація
Нехай функція визначена в деякому околі точки . Якщо функція неперервна в точці , для неї виконується означення неперервності. Якщо хоча б одна з рівностей (2.15) порушується, говорять, що функція в точці терпить розрив, а сама точка називається точкою розриву.
Якщо односторонні границі функції в
точці
рівні, але не дорівнюють значенню функції
в точці, тобто
![]() ,
говорять, що в точці
усувний розрив. Прикладом такого розриву
є розрив функції
,
говорять, що в точці
усувний розрив. Прикладом такого розриву
є розрив функції
![]() в точці
в точці
![]() .
Дійсно, функція визначена, а значить і
неперервна для всіх
,
крім
.
Дійсно, функція визначена, а значить і
неперервна для всіх
,
крім
![]() .
У самій точці
функція не визначена, але
.
У самій точці
функція не визначена, але
![]() ,
отже, маємо усувний розрив. Досить
довизначити функцію в точці
,
поклавши
,
отже, маємо усувний розрив. Досить
довизначити функцію в точці
,
поклавши
![]() .
Нова функція
.
Нова функція

неперервна в точці і на всій числовій прямій.
Якщо односторонні границі функції в
точці
різні, але обидві скінченні, то говорять,
що в цій точці розрив першого роду.
Наприклад, функція
 не визначена в точці
.
не визначена в точці
.
Обчислимо односторонні границі функції в зазначеній точці, використовуючи символічні записи:
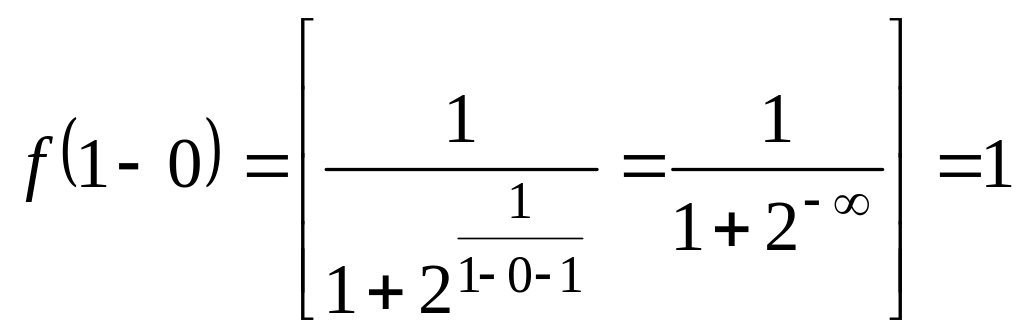 ,
,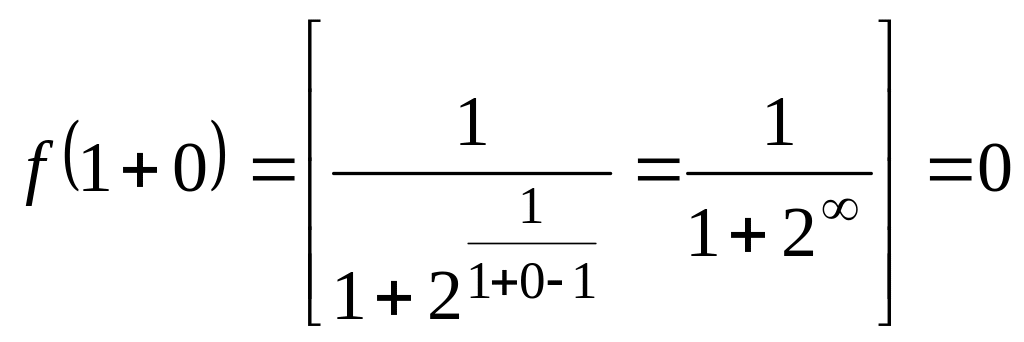 .
.
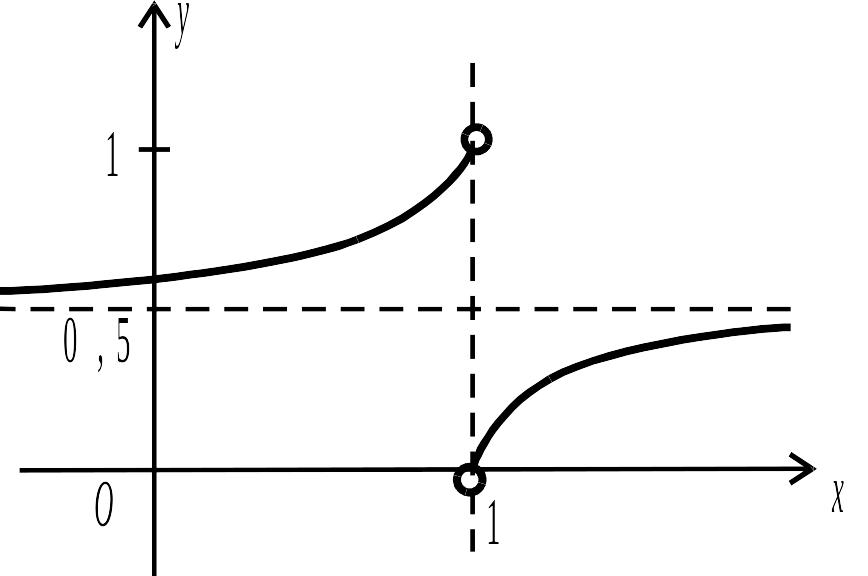
Отже, в точці функція терпить розрив першого роду. Графік такої функції зображений на рис. 2.32.
|
|
Рис. 2.32. |
Рис. 2.33. |
Розрив першого роду називають розривом зі скінченним стрибком.
Якщо ж хоча б одна з однобічних границь функції в точці дорівнює нескінченності, говорять, що в точці розрив другого роду або розрив з нескінченним стрибком.
Такий розрив має функція в точці .Дійсно:
Рис. 2.34.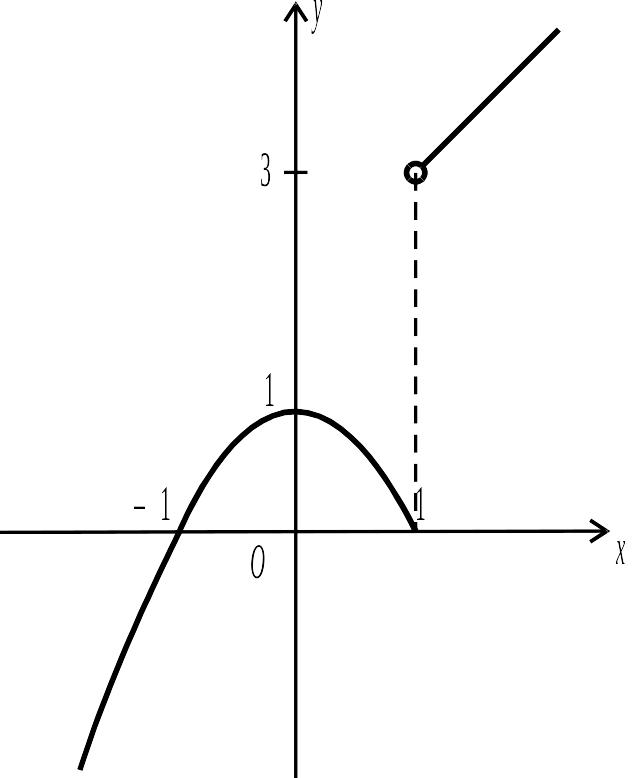
![]() ;
;
![]()
Графік функції зображений на рис. 2.33.
Приклад 2.13. Дослідити на неперервність функцію:
![]()
Розв’язання.
Оскільки всі елементарні функції
неперервні в кожній точці своєї області
визначення, функції
![]() і
і
![]() неперервні на всій числовій прямій.
Досліджуємо точку x=1. Обчислимо
односторонні границі функції в точці:
неперервні на всій числовій прямій.
Досліджуємо точку x=1. Обчислимо
односторонні границі функції в точці:
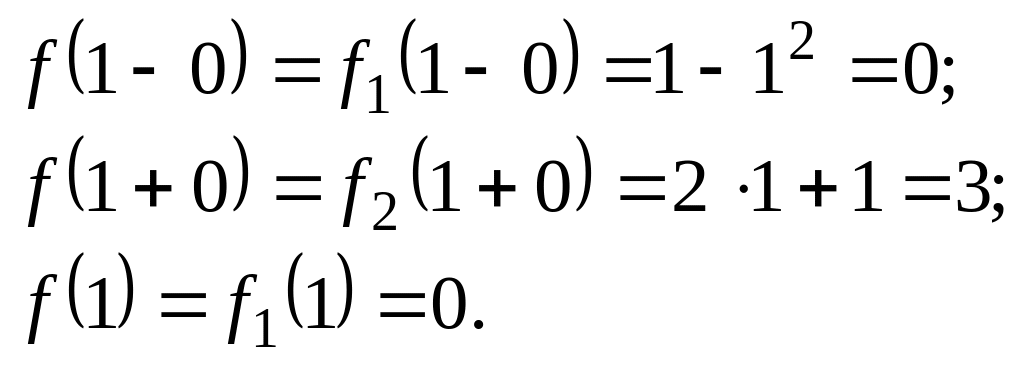
Отже, задана в умові функція неперервна в кожній точці числової прямої, крім точки x=1. У точці x=1 функція терпить розрив першого роду. Графік функції зображений на рис. 2.34.
20. Властивості функцій, неперервних на відрізку
Будемо називати функцію неперервною
на відрізку
![]() ,
якщо вона неперервна в кожній точці
інтервалу
,
якщо вона неперервна в кожній точці
інтервалу
![]() ,
неперервна справа в точці
і неперервна зліва в точці
.
,
неперервна справа в точці
і неперервна зліва в точці
.
Теорема
2.10. Якщо функція
неперервна на відрізку
,
то вона набуває на цьому відрізку
найбільшого
і найменшого
значення, тобто для всіх точок відрізка
виконується нерівність:
![]() .
.
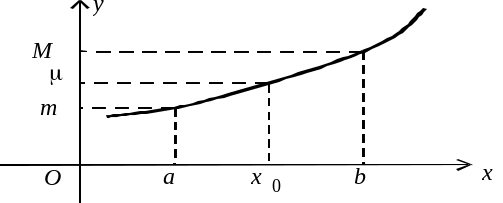
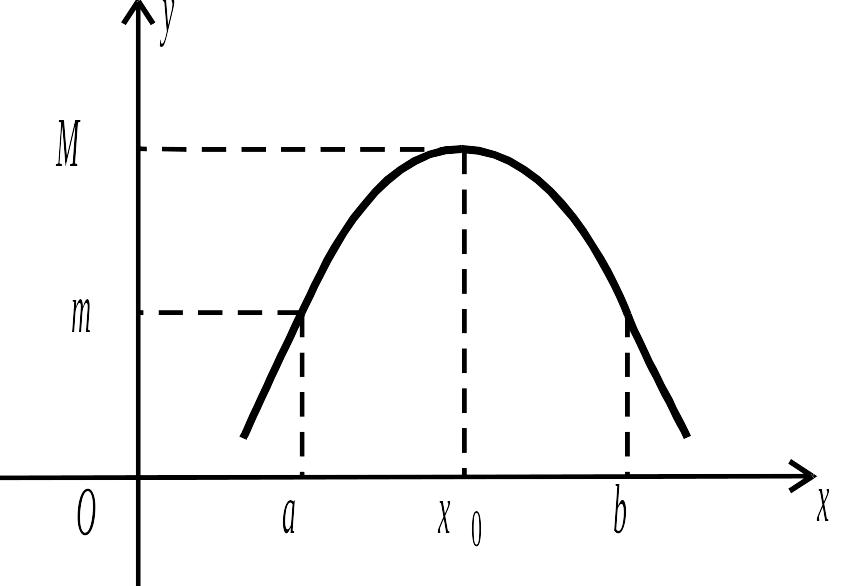
Якщо функція монотонна на відрізку , то такі значення збігаються зі значеннями функції на кінцях відрізка (рис. 2.35), якщо не монотонна – чи (чи обидва) можуть знаходитися в деякій внутрішній точці відрізка (рис. 2.36).
|
|
Рис. 2.35. |
Рис. 2.36. |
Свої найбільше і найменше значення
функція може приймати і кілька разів.
Так, функція
![]() на відрізку
на відрізку
![]() кілька разів набуває значення
кілька разів набуває значення
![]() і
і
![]() .
.
Теорема
2.11. Якщо функція
неперервна на відрізку
,
то для будь-якого числа![]() ,
взятого між найменшим
і найбільшим
значеннями функції на відрізку, усередині
відрізка знайдеться хоча б одна така
точка
,
що значення функції в зазначеній точці
буде дорівнювати
.
,
взятого між найменшим
і найбільшим
значеннями функції на відрізку, усередині
відрізка знайдеться хоча б одна така
точка
,
що значення функції в зазначеній точці
буде дорівнювати
.
Якщо функція монотонна на відрізку , то така точка єдина , якщо не монотонна – знайдеться кілька точок, значення функції в яких дорівнюватиме заданому числу.
Теорема 2.12. Якщо функція неперервна на відрізку і на кінцях відрізка набуває значення різних знаків, то у середині відрізка знайдеться хоча б одна така точка, значення функції в якій дорівнює нулю (рис. 2.37).
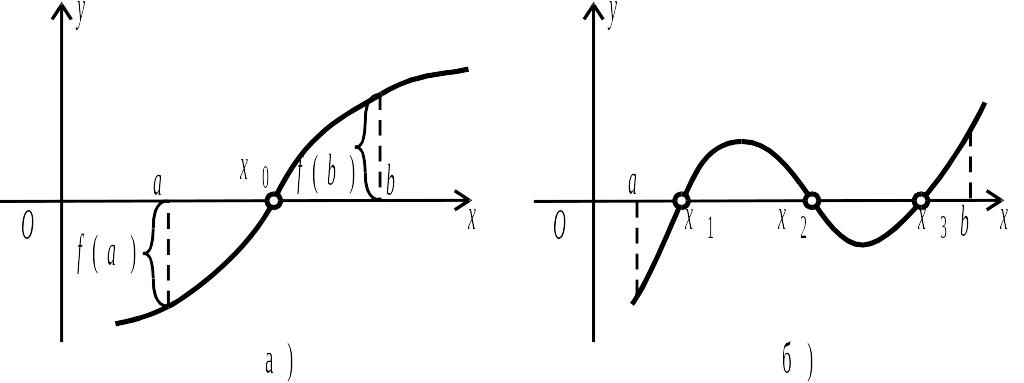
Рис. 2.37.
Говорять, якщо функція на кінцях відрізка набуває значення різних знаків, але на цьому відрізку в неї існує хоча б один корінь.
Теорема невірна, якщо функція на відрізку не є неперервною.
Теорема широко застосовується в наближених розв'язках рівнянь, оскільки є ознакою існування кореня функції на зазначеному відрізку.
Наприклад, рівняння
![]() має на відрізку
має на відрізку
![]() хоча б один дійсний корінь, оскільки
для
хоча б один дійсний корінь, оскільки
для
![]()
![]() ,
,
![]() .
.
Вправи
2.1. Знайти область визначення функцій:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; є)
; є)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
і)
![]() ; к)
; к)
![]() .
.
2.2. З'ясувати, які функції є парними, які непарними:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; є)
; є)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
і)
![]() ; к)
; к)
![]() .
.
2.3. Знайти область значень функцій:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
![]() ; д)
; д)
![]() .
.
2.4. Знайти найменший період функцій або довести їх неперіодичність:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ; д)
; д)
![]() .
.
2.5. Відомо, що
![]() .
Знайти
.
Знайти
![]() .
.
2.6. Відомо, що
![]() .
Знайти
.
Знайти
![]() .
.
2.7. Відомо, що
![]() ,
,
![]() .
Знайти
.
Знайти
![]() .
.
2.8. Знайти функцію, обернену до даної і побудувати графік даної і оберненої до неї функції:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
2.9. Побудувати графіки елементарних функцій:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; є)
; є)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
і)
![]() ,
де
,
де
![]() – ціла частина
;
– ціла частина
;
к)
![]() ,
де
,
де
![]() – дробова частина
;
– дробова частина
;
л)
![]() ; м)
; м)
![]() ;
;
н)
![]() ; о)
; о)
![]() .
.
2.10. Оптимальну швидкість (м/с) обертання молотильного барабана кукурудзомолотарки визначають за формулою
![]()
де
x
– вологість зерна у відсотках. Знайти![]() і
і
![]() .
Знайти область визначення функції.
Побудувати графік функції. Як змінюється
швидкість барабана зі збільшенням
вологості зерна?
.
Знайти область визначення функції.
Побудувати графік функції. Як змінюється
швидкість барабана зі збільшенням
вологості зерна?
2.11. При
будівництві ставків необхідно враховувати
кількість води, що буде надходити в
ставок під час весняного паводка. Вона
прямо пропорційна величині
![]() ,
де
,
де
![]() ,
,
– відповідно відсоток озерності і
заболоченості місцевості. Розв’язати
нерівність
,
,
– відповідно відсоток озерності і
заболоченості місцевості. Розв’язати
нерівність
![]() ,
побудувати відповідну частину графіка
(вибрати по осі абсцис масштаб 1:10, а по
осі ординат 1:0,1).
,
побудувати відповідну частину графіка
(вибрати по осі абсцис масштаб 1:10, а по
осі ординат 1:0,1).
2.12. Валова продукція на 1 га сільськогосподарських угідь за чотири роки збільшилася на 24,4% . Скласти рівняння прямої, що відображає зміну валової продукції на 1 га протягом чотирьох років за умови, що валова продукція у відсотках змінюється пропорційно часу.
2.13. Витрати виробництва на 10 одиниць деякого товару складають 1000 грош. од., на 50 одиниць товару – 2000 грош. од. Визначити витрати виробництва на 30 одиниць товару за умови, що витрати залежать від об'єму продукції лінійно.
2.14. Перевезення вантажу з даного міста в перший пункт, що знаходиться на відстані 100 км, коштує 200 грош. од., а в інший, що знаходиться на відстані 400 км, – 350 грош. од. Встановити залежність вартості перевезення у від відстані х, якщо вартість є лінійна функція від відстані (якість доріг не враховується).
2.15. Скласти рівняння прямої, що відображає зміну врожайності 1 га протягом сімнадцяти років, якщо в перший рік з 1 га було зібрано 9,1 ц зернових культур, а в останній рік – 21 ц.
2.16. Припускається, що вартість машини, що переноситься на вартість виготовленої з її допомогою продукції, залежить від часу експлуатації t. Нехай первісна вартість у = 25 тис. грош. од., а термін роботи до повного зносу – 10 років. Побудувати лінію залежності вартості машини від терміну її служби. Чому буде дорівнювати вартість машини через 8 років?
2.17. Витрати перевезень двома видами транспорту виражаються функціями: у = 50х + 150, у = 25х + 250, де х – відстань перевезень, км; у – транспортні витрати, грош. од. При яких відстанях економніше користатися першим видом транспорту?
2.18. Побудувати криві байдужності
функції корисності
![]() при рівнях корисності, рівних 2 і 3. Знайти
їх асимптоти.
при рівнях корисності, рівних 2 і 3. Знайти
їх асимптоти.
2.19. Навести приклад функції, що описує бюджетне обмеження. Знайти її точки перетину з осями координат.
2.20. Навести приклад функції, що описує залежність величини попиту від доходу.
2.21. Навести приклад функції, що описує залежність пропозиції від ціни. Побудувати її графік.
2.22. Залежність рівня потреб у деякого
виду товарів від рівня доходу сім’ї
виражається
формулою:
![]() .
Знайти рівень потреб товарів при рівні
доходу сім’ї 158 грош. од., якщо відомо,
що при
.
Знайти рівень потреб товарів при рівні
доходу сім’ї 158 грош. од., якщо відомо,
що при
![]()
![]() ;
при
;
при
![]()
![]() ;
при
;
при
![]()
![]() .
.
2.23. Побудувати графіки функцій
![]() ,
заданих параметрично, якщо:
,
заданих параметрично, якщо:
а)
![]() ,
,
![]() ; б)
; б)
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ; г)
; г)
![]() ,
,
![]() .
.
2.24. Побудувати графіки функцій, заданих неявно:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
2.25. Побудувати графіки функцій
![]() в полярній системі координат:
в полярній системі координат:
а)
![]() (спіраль Архімеда); б)
(спіраль Архімеда); б)
![]() (гіперболічна спіраль);
(гіперболічна спіраль);
в)
![]() (кардіоїда); г)
(кардіоїда); г)
![]() ;
;
д)
![]() (лемніската Бернуллі).
(лемніската Бернуллі).
2.26. Довести, користуючись означенням, що послідовність є нескінченно малою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
2.27. Довести, користуючись означенням, що послідовність є нескінченно великою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ,
,
![]() .
.
2.28. Довести рівності:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ,
,
![]() ; г)
; г)
![]() ,
;
,
;
д)
![]() ,
,
![]() ; є)
; є)
![]() .
.
2.29. Знайти найбільший елемент послідовності:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
2.30. Знайти найменший елемент послідовності:
а)
![]() ;
б)
;
б)
![]() .
.
2.31. Для послідовності
знайти
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
якщо:
,
якщо:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() .
.
2.32.–2.56. Знайти границі послідовностей:
2.32.
![]() ; 2.33.
; 2.33.
![]() ;
;
2.34.
![]() ; 2.35.
; 2.35.
![]() ;
;
2.36.
![]() ; 2.37.
; 2.37.
![]() ;
;
2.38.
![]() ; 2.39.
; 2.39.
![]() ;
;
2.40.
![]() ; 2.41.
; 2.41.
![]() ;
;
2.42.
![]() ;
;
2.43.
![]() ;
;
2.44.
![]() ;
;
2.45.
![]() ; 2.46.
; 2.46.
![]() ;
;
2.47.
![]() ; 2.48.
; 2.48.
![]() ;
;
2.49.
![]() ;
;
2.50.
![]() ;
;
2.51.
![]() ;
;
2.52.
![]() ;
;
2.53.
![]() ;
;
2.54.
![]() ;
;
2.55.
![]() ;
;
2.56.
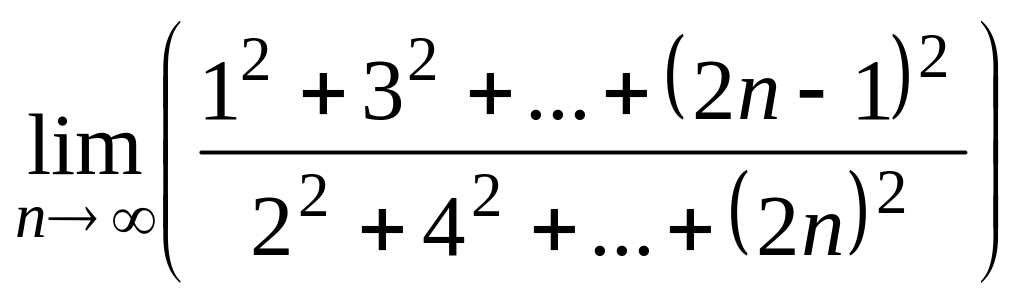 .
.
2.57. Нехай
початковий внесок
![]() тис. грош. од. вкладено на чотири роки
під складні відсотки при ставці 100%
річних. Знайти нарощене значення внеску
за роками.
тис. грош. од. вкладено на чотири роки
під складні відсотки при ставці 100%
річних. Знайти нарощене значення внеску
за роками.
2.58. Нехай 3 млн. грош. од. видано в кредит на 6 місяців під прості відсотки за ставкою 10% за місяць. Знайти нарощене значення боргу наприкінці кожного місяця.
2.59. Суму 2000
грош. од. покладено в банк під схему
неперервного нарахування відсотків
при ставці 10% за рік. Знайти нарощену
наприкінці кожного року суму
![]() при
при
![]() ,
2, 3, 5 і 10.
,
2, 3, 5 і 10.
2.60. При одній і тій же процентній ставці при схемі неперервного нарахування відсотків вкладник С через 2 роки одержує 1000 грош. од., вкладник D через 4 роки одержує 600 грош. од. Знайти процентну ставку q, якщо початковий внесок вкладника С удвічі більше, ніж вкладника D.
2.61. Суму в 5 млн. грош. од. видано в кредит на 10 місяців під прості відсотки за ставкою 15% на місяць. Знайти нарощене значення боргу наприкінці кожного місяця.
2.62. Сума 600 тис. грош. од. інвестується на 5 років під складні відсотки за ставкою 80% річних. Знайти нарощену суму за цей термін.
2.63. Вклад 10 тис. грош. од. покладено
в банк під складні відсотки терміном
на 5 років. Обчислити кінцеву суму, якщо
відсотки нараховуються наприкінці
кожного кварталу за нормою
![]() .
.
2.64. Розв’язати задачу 2.63 в припущені, що відсотки нараховуються неперервно. Порівняти результати.
2.65. Знайти складні відсотки за півтора роки, нараховані на 900 тис. грош. од. за ставкою 22% в квартал.
2.66. На терміновий вклад у банку зараховано 200 грош. од. за ставкою 5% річних. Знайти накопичені суми через 2б 3б 4б 5 років за умови:
а) нарахування простих відсотків;
б) нарахування складних відсотків;
в) неперервного нарахування відсотків.
2.67. Знайти початкове значення інвестиції, якщо нарощена сума до кінця п’ятого року становить 10 млн. грош. од. Відсотки нараховуються за такими ставками:
а) 100% наприкінці кожного року;
б) 50% наприкінці кожного півріччя;
в) 25% наприкінці кожного кварталу.
2.68. Довести,
користуючись означенням границі функції,
що
![]() .
.
2.69.–2.112. Обчислити границі функцій
2.69.
![]() . 2.70.
. 2.70.
![]() .
.
2.71.
![]() . 2.72.
. 2.72.
![]() .
.
2.73.
![]() . 2.74.
. 2.74.
![]() .
.
2.75.
![]() . 2.76.
. 2.76.
![]() .
.
2.77.
![]() . 2.78.
. 2.78.
![]() .
.
2.79.
![]() . 2.80.
. 2.80.
![]() .
.
2.81.
![]() . 2.82.
. 2.82.
![]() .
.
2.83.
![]() . 2.84.
. 2.84.
![]() .
.
2.85.
![]() . 2.86.
. 2.86.
![]() .
.
2.87.
![]() . 2.88.
. 2.88.
![]() .
.
2.89.
![]() . 2.90.
. 2.90.
![]() .
.
2.91.
![]() . 2.92.
. 2.92.
![]() .
.
2.93.
![]() . 2.94.
. 2.94.
![]() .
.
2.95.
![]() . 2.96.
. 2.96.
![]() .
.
2.97.
![]() . 2.98.
. 2.98.
![]() .
.
2.99.
![]() . 2.100.
. 2.100.
![]() .
.
2.101.
![]() . 2.102.
. 2.102.
![]() .
.
2.103.
![]() . 2.104.
. 2.104.
![]() .
.
2.105.
![]() . 2.106.
. 2.106.
![]() .
.
2.107.
![]() . 2.108.
. 2.108.
![]() .
.
2.109.
![]() . 2.110.
. 2.110.
![]() .
.
2.111.
![]() . 2.112.
. 2.112.
![]() .
.
2.113. Довести,
що функції
![]() та
та
![]() при
при
![]() є нескінченно малими одного порядку.
є нескінченно малими одного порядку.
2.114. Довести,
що нескінченно малі при
функції
![]() та
та
![]() еквівалентні.
еквівалентні.
2.115.–2.120. Обчислити границі, використовуючи еквівалентні нескінченно малі.
2.115.
![]() . 2.116.
. 2.116.
![]() .
.
2.117.
![]() . 2.118.
. 2.118.
![]() .
.
2.119.
![]() . 2.120.
. 2.120.
![]() .
.
2.121. Знайти асимптоти і побудувати наступні криві:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
![]() ; д)
; д)
![]() .
.
2.122. Нехай
![]() .
Визначити порядок малості відносно
змінної
наступних функцій:
.
Визначити порядок малості відносно
змінної
наступних функцій:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
2.123. Довести неперервність функцій у своїй області визначення:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
![]() ; д)
; д)
![]() .
.
2.124. Дослідити на неперервність функції і визначити характер точок розриву, побудувати графік функції:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
![]() д)
д)

є)
![]() ; ж)
; ж)
![]() ; з)
; з)
![]() ;
;
і)
![]() ; к)
; к)
![]() ;
;
л)
![]() м)
м)
![]()
н)
![]() о)
о)
![]()
п)
![]() р)
р)
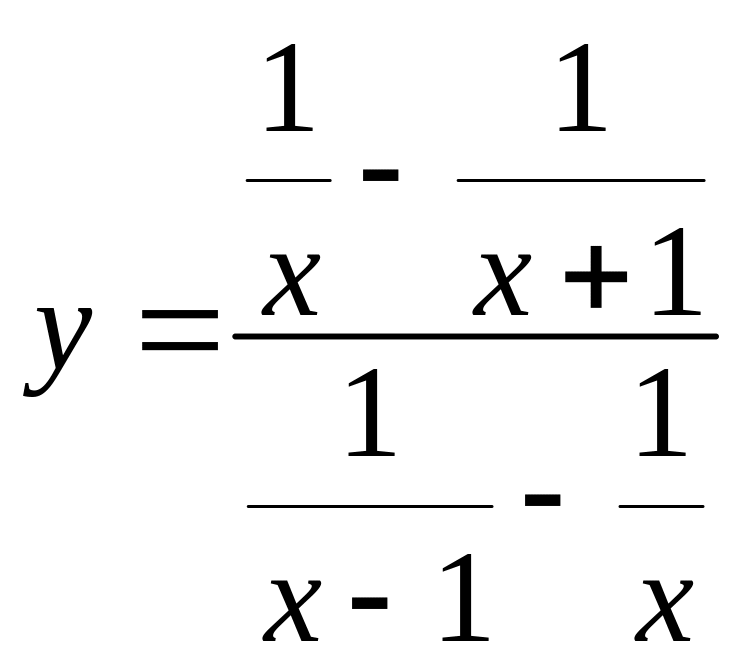 ;
;
с)
![]() т)
т)
![]() .
.
2.125. Чи може
функція
![]() на відрізку [1;3] набувати значення, рівне
10?
на відрізку [1;3] набувати значення, рівне
10?
2.126. Чи має
рівняння
![]() корені на відрізках:
корені на відрізках:
а) [0;1]; б) [1;2]; в) [2;3].