
- •Розділ 1. Теорія множин
- •1. Поняття множини
- •2. Найпростіші операції над множинами
- •3. Числові множини
- •4. Обмежені множини. Верхні та нижні грані множин
- •5. Поняття функції (відображення)
- •6. Еквівалентні множини. Потужність множин
- •7. Потужність континуума
- •Розділ 2. Послідовності. Функції однієї змінної
- •1. Числові послідовності
- •2. Границя послідовності
- •3. Застосування послідовностей в економіці
- •4. Поняття функції
- •5. Способи задання функції
- •6. Деякі властивості функцій
- •7. Функція, обернена до даної
- •8. Класифікація функцій
- •9. Основні методи побудови графіків функцій
- •10. Приклади застосування функцій в економіці
- •11. Границя функції
- •12. Нескінченно малі і нескінченно великі функції
- •13. Основні теореми про границі функцій
- •14. Обчислення границь функцій
- •15. Істотні границі Перша істотна границя
- •Друга істотна границя
- •16. Порівняння нескінченно малих
- •17. Неперервність функції в точці
- •18. Властивості функцій, неперервних в точці
- •19. Точки розриву і їхня класифікація
- •20. Властивості функцій, неперервних на відрізку
- •Розділ 3. Диференціальне числення функції однієї змінної
- •1. Задачі, що приводять до поняття похідної функції
- •2. Поняття похідної
- •3. Геометричний зміст похідної. Рівняння дотичної і нормалі до кривої
- •4. Диференційованість функції в точці
- •5. Похідні елементарних функцій
- •6. Основні правила диференціювання
- •7. Похідна складної функції
- •8. Логарифмічне диференціювання. Похідна степеневої, показникової, показниково-степеневої функцій
- •9. Похідна оберненої функції. Похідні обернених тригонометричних функцій
- •10. Таблиця похідних
- •11. Похідна неявно заданої функції
- •12. Похідна функції, заданої параметрично
- •13. Похідні вищих порядків
- •14. Наближені обчислення за допомогою похідної
- •15. Еластичність функції
- •Еластичності елементарних функцій:
- •16. Застосування еластичності в економічному аналізі Еластичність попиту відносно ціни
- •Еластичність і податкова політика
- •17. Основні теореми диференціального числення
- •18. Правило Лопіталя
- •19. Зростання і спадання функції на проміжку
- •20. Екстремуми функції
- •Необхідна умова екстремуму диференційованої функції.
- •Перша достатня умова екстремуму.
- •Друга достатня умова екстремуму.
- •Третя достатня умова екстремуму.
- •21. Найбільше і найменше значення функції на відрізку
- •22. Випуклість, увігнутість графіка функції. Перегин
- •Необхідна і достатня умова випуклості (увігнутості) графіка функції.
- •Необхідна умова точки перегину.
- •Достатні умови точки перегину.
- •23. Асимптоти графіка функції
- •24. Повне дослідження і побудова графіка функції
- •25. Застосування похідної в економіці Граничний аналіз в економіці.
- •Задачі на екстремум.
- •Розділ 4. Диференціальне числення функції багатьох змінних
- •1. Основні поняття
- •2. Границя і неперервність
- •3. Частинні похідні функції
- •4. Повний диференціал
- •5. Похідна функції за даним напрямком. Градієнт
- •6. Частинні похідні і диференціали вищих порядків
- •7. Локальний екстремум функції багатьох змінних
- •8. Неявно задані функції
- •9. Умовний екстремум
- •10. Найбільше і найменше значення функції в області
- •11. Метод найменших квадратів
- •12. Економічні задачі
15. Істотні границі Перша істотна границя
Розглянемо границю
![]() .
Функція
.
Функція
![]() парна,
парна,
![]() .
За умовою
,
тому досить розглянути значення x,
що задовольняють нерівності
.
За умовою
,
тому досить розглянути значення x,
що задовольняють нерівності
![]() .
.
Візьмемо дугу кола радіуса
і кут, радіанна міра якого дорівнює
(рис. 2.31). На рис. 2.31:
![]()
Рис. 2.31.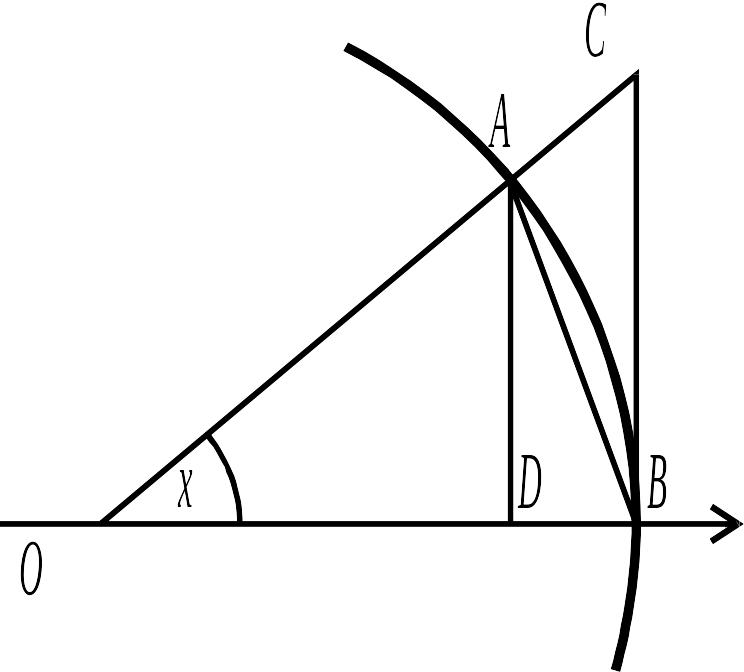
![]() ,
сектора
і трикутника
,
сектора
і трикутника
![]() ,
що відповідно дорівнюють
,
що відповідно дорівнюють
![]() ,
,
![]() ,
,
![]() або
або
![]() ,
,
![]() ,
,
![]() .
Очевидно
.
Очевидно
![]() ,
звідки
,
звідки
![]() .
Розділимо останні нерівності на
.
Розділимо останні нерівності на
![]() і одержимо
і одержимо
![]() ,
,
![]() .
.
Функція
розташована між функціями
![]() і
і
![]() ,
причому
,
причому
![]() ,
тому за теоремою 2.5 одержимо
,
тому за теоремою 2.5 одержимо
![]() . (2.5)
. (2.5)
Границя (2.5) називається першою істотною границею. Використовуючи першу істотну границю можна показати, що
![]() . (2.6)
. (2.6)
Дійсно,
![]() ,
,
і також
![]() . (2.7)
. (2.7)
Замінимо
![]() ,
звідки
,
звідки
![]() ,
причому при
,
,
причому при
,
![]() .
Одержимо
.
Одержимо
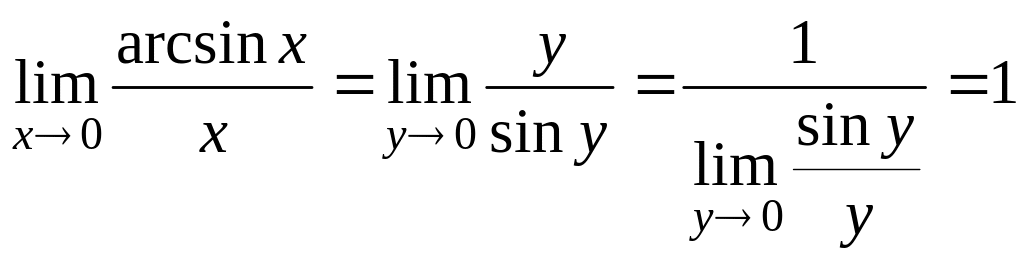 .
.
Аналогічно, ![]() . (2.8)
. (2.8)
Границі 2.5–2.8 допомагають розкрити невизначеність у випадку, якщо під знаком границі тригонометричні функції.
Приклад
2.10. Обчислити
![]() .
.
Розв’язання.
Безпосередньою підстановкою замість
граничного значення одержуємо
невизначеність
.
Перетворимо даний дріб, застосувавши
формулу
![]() ,
одержимо
,
одержимо
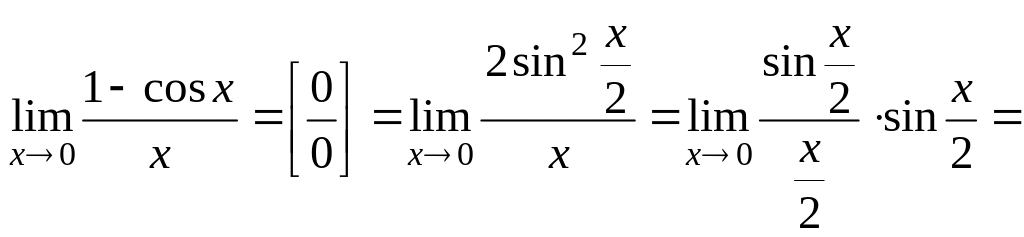
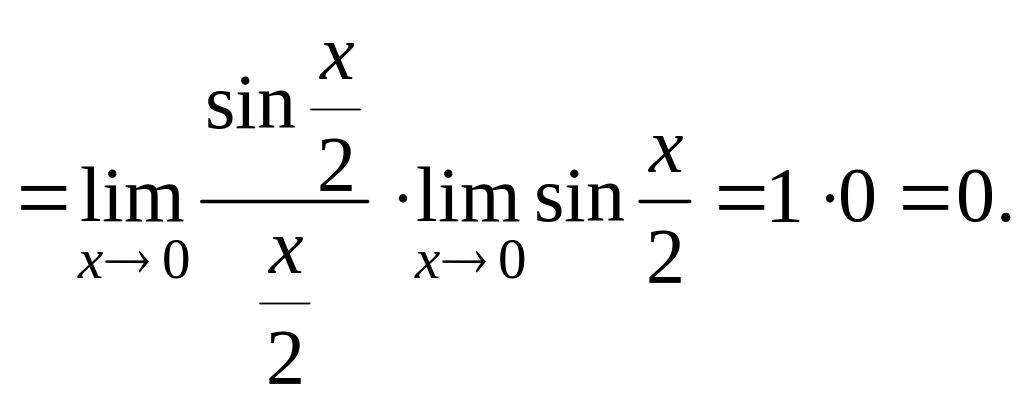
Друга істотна границя
Границю виду:
![]() (2.9)
(2.9)
називають другою істотною границею.
Можна використовуючи границю (2.9) показати, що:
![]() ; (2.10)
; (2.10)
![]() ; (2.11)
; (2.11)
![]() . (2.12)
. (2.12)
Приклад
2.11. Обчислити
![]() .
.
Розв’язання. Маємо
![]() .
.
16. Порівняння нескінченно малих
Нескінченно малі функції часто порівнюють між собою за швидкістю їхнього наближення до нуля. Нехай і нескінченно малі функції при .
Якщо
![]() ,
то говорять, що нескінченно мала
більш високого порядку, швидше наближається
до нуля, ніж
,
або
нескінченно мала більш низького порядку,
ніж
при
.
,
то говорять, що нескінченно мала
більш високого порядку, швидше наближається
до нуля, ніж
,
або
нескінченно мала більш низького порядку,
ніж
при
.
Якщо
![]() ,
то
і
називаються нескінченно малими одного
порядку. Зокрема, якщо
,
то
і
називаються нескінченно малими одного
порядку. Зокрема, якщо
![]() ,
то
і
називаються еквівалентними нескінченно
малими при
.
Той факт, що
й
еквівалентні, записують так:
,
то
і
називаються еквівалентними нескінченно
малими при
.
Той факт, що
й
еквівалентні, записують так:
![]() при
.
при
.
Наприклад, функції
![]() ,
,
![]() при
є нескінченно малими одного порядку,
оскільки
при
є нескінченно малими одного порядку,
оскільки
![]() ;
функція
;
функція
![]() є нескінченно малою більш високого
порядку, ніж
,
оскільки
є нескінченно малою більш високого
порядку, ніж
,
оскільки
![]() ;
функції
;
функції
![]() і
є еквівалентними при
,
оскільки
і
є еквівалентними при
,
оскільки
![]() .
Аналогічно можна показати, що при
.
Аналогічно можна показати, що при
![]()
![]()
![]()
![]()
![]() .
.
Теорема
2.6. Границя відношення нескінченно
малих не змінюється при заміні їх
еквівалентними нескінченно малими:
якщо
![]() ,
,
![]() ,
то
,
то
![]() .
.
Дійсно, помножимо і розділимо відношення
![]() послідовно на
послідовно на
![]() і
і
![]() ,
одержимо
,
одержимо
![]() оскільки
оскільки
![]() .
.
При обчисленні границь часто буває корисно замінити нескінченно малу в чисельнику чи знаменнику дробу більш простою, еквівалентною їй нескінченно малою функцією.
Приклад
2.12. Обчислити
![]() .
.
Розв’язання.
Оскільки при
функції
![]() ,
,
![]() – нескінченно малі, замінимо їхніми
еквівалентами:
– нескінченно малі, замінимо їхніми
еквівалентами:
![]() ,
,
![]() .
Тоді
.
Тоді
![]() .
.
17. Неперервність функції в точці
Означення 2.11. Функція називається неперервною в точці , якщо вона визначена в точці та її околі, існує границя функції при , і ця границя співпадає зі значенням функції в точці , тобто
![]() . (2.13)
. (2.13)
Рівність (2.13) можна записати у вигляді
![]() ,
,
що дає можливість зробити наступний висновок: для функції, неперервної в точці, знаки функції і границі можна переставляти. Говорять, із границею можна переходити під знак функції. Наприклад,
![]() .
.
З виразу (2.13) на підставі теореми 2.2
випливає, що
![]() чи
чи
![]() ,
де
функція нескінченно мала при
або
,
де
функція нескінченно мала при
або
![]() .
.
Назвемо різницю
приростом аргументу, а різницю
![]() приростом функції. Введемо позначення:
приростом функції. Введемо позначення:
![]() ;
;
![]() .
Тоді можна сформулювати інше означення
функції, неперервної в точці.
.
Тоді можна сформулювати інше означення
функції, неперервної в точці.
Означення 2.12. Функція називається неперервною в точці , якщо вона визначена в т. і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції, тобто
![]() . (2.14)
. (2.14)
Означення 2.12 дає можливість стверджувати, що всі основні елементарні функції неперервні в кожній точці своєї області визначення.
Наприклад, для функції
![]() приріст в точці
:
приріст в точці
:
![]() .
Тоді:
.
Тоді:
![]()
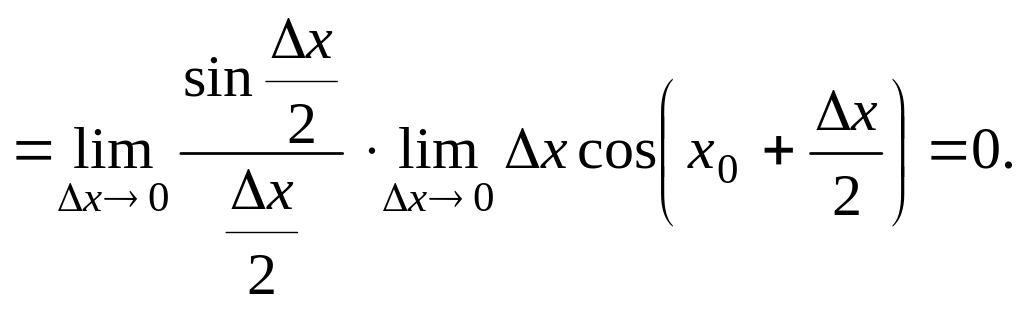
А це значить, що функція
![]() неперервна в кожній точці своєї області
визначення.
неперервна в кожній точці своєї області
визначення.
Означення 2.13. Функція називається неперервною в точці , якщо вона визначена в точці , і границя функції в точці ліворуч дорівнює границі функції в точці праворуч і дорівнює значенню функції в точці. Записують так:
![]() , (2.15)
, (2.15)
або символічно
![]() .
.
