99. 11. Границя функції

Нехай функція визначена в деякому околі точки , крім, може бути, самої точки . В точці функція може бути і не визначена.

Означення 2.7. Число називається границею функції при , якщо для будь-якої числової послідовності значень аргументу відповідна послідовність значень функції прямує до числа . Позначають границю функції так: .

При цьому припускається, що послідовність належить області визначення функції.

Суть цього означення полягає в тому, що, як тільки значення аргументу необмежено близько наближаються до значення , відповідні значення функції необмежено близько наближаються до значення .

Більш строгим є наступне означення границі.

Означення 2.8. Число A називається границею функції при прямуючому до , якщо для кожного скільки завгодно малого наперед заданого додатного числа можна вказати таке додатне число , що як тільки , то виконується умова .

Оскільки нерівність визначає –окіл точки на вісі абсцис, а нерівність визначає –окіл точки на вісі ординат, геометричний зміст означення 2.8 такий: для будь-якого –околу точки на вісі можна знайти такий –окіл точки на вісі , що як тільки значення аргументу попадає в –окіл точки , відповідне значення функції попадає в –окіл точки .

Приклад 2.6. Довести, виходячи з означення границі функції, що .

Розв’язання. Нехай – будь-яке, як завгодно мале, додатне число. Знайдемо таке , щоб для всіх , що задовольняють нерівність , виконувалася нерівність

або .

Очевидно, що , оскільки при такому  умова приводить до виконання умови , з чого випливає, що .

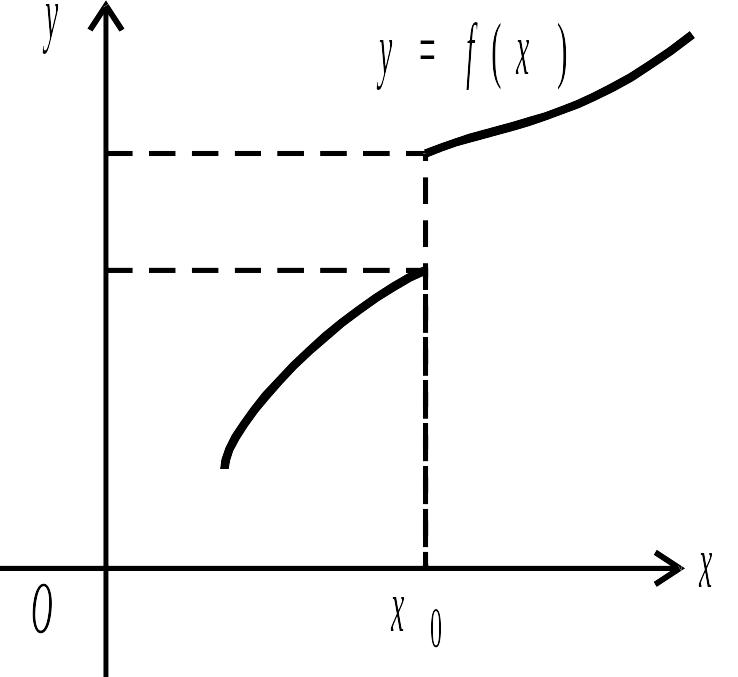
Рис. 2.28.

Якщо розглянути графік функції, зображений на рис. 2.28, то стане ясно, що ця функція не має границі при . У такій ситуації говорять про односторонні границі функції. Якщо за умови, що значення аргументу прямують до , залишаючись менше , число A називають границею функції в точці зліва, і пишуть . Аналогічно, якщо за умови, що, залишаючись більше , то називають правосторонньою границею функції в точці , і пишуть .

Якщо однобічні границі функції в точці існують і рівні, то функція має границю, і вона дорівнює загальному значенню цих границь.

Говорять, що границя функції при дорівнює нескінченності, якщо для кожного як завгодно великого додатного числа можна вказати таке додатне число , що для всіх , які задовольняють нерівність , виконується умова . У цьому випадку пишуть (рис. 2.29).

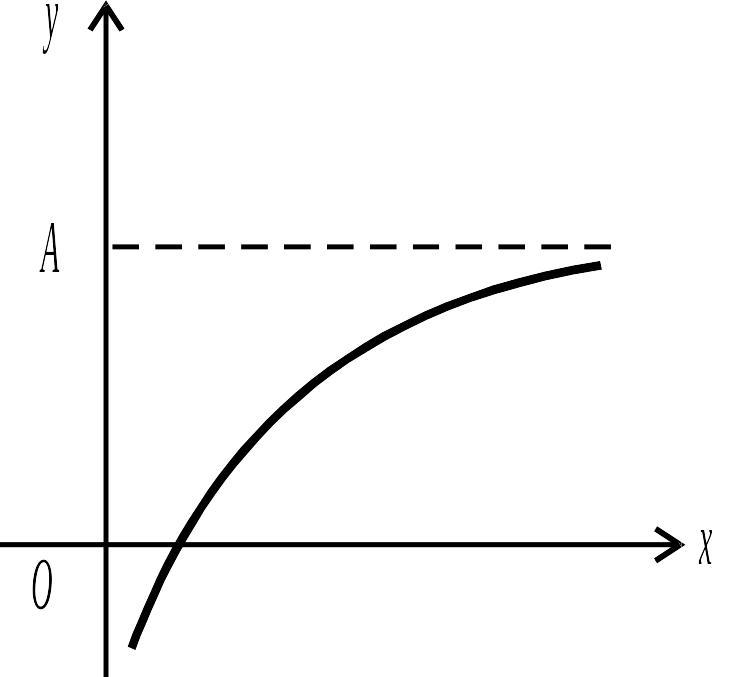
Функція має границею число A при , якщо для будь-якого, скільки завгодно малого , можна вказати таке число , що для всіх , які задовольняють нерівність виконується нерівність (рис. 2.30). Пишуть .

Рис. 2.29.	Рис. 2.30.

100. 12. Нескінченно малі і нескінченно великі функції

Означення 2.9. Функція називається нескінченно малою при ( – число або один із символів , , ), якщо для кожного, як завгодно малого наперед заданого додатнього числа можна вказати таке додатне число , що для всіх , які задовольняють нерівність , виконується умова . Тобто, функція є нескінченно малою при , якщо .

Наприклад, , при є нескінченно малою, її значення можуть бути менше будь-якого наперед заданого числа, а при її значення прагнуть до числа 9, у чому легко переконатися підстановкою у функцію окремих частинних значень.

Означення 2.10. Функція називається нескінченно великою при ( – число або один із символів , , ), якщо .

Наприклад, функція при може приймати як завгодно великі значення, отже, у зазначених умовах вона є нескінченно великою.

Нескінченно малі і нескінченно великі функції мають такі властивості.

Властивість 1. Алгебраїчна сума скінченного числа нескінченно малих при функцій є функцією нескінченно малою.

Нехай і – нескінченно малі при функції.

Це значить, що для кожного, як завгодно малого, наперед заданого додатного числа знайдуться такі додатні і , що при , виконається умова , а при виконається умова . Виберемо менше з чисел і ( ) і оцінимо :

.

А це значить, що функція нескінченно мала при .

Властивість 2. Добуток обмеженої функції на нескінченно малу при є функція нескінченно мала.

Нехай функція обмежена, тобто знайдеться таке додатне число , що , а функція – нескінченно мала при : яке б як завгодно мале не взяли, знайдеться таке додатне число , що для усіх виконається умова . Оцінимо , що і потрібно було довести.

Наприклад, при добуток є функцією нескінченно малою, оскільки функція , обмежена.

Наслідок 1. Добуток сталої на нескінченно малу функцію є функція нескінченно мала.

Наслідок 2. Добуток скінченного числа нескінченно малих при функцій є функцією нескінченно малою.

Дійсно, нескінченно мала при функція в околі точки є обмеженою.

Властивість 3. Сума нескінченно великих при функцій є функцією нескінченно великою.

Відзначимо, що для різниці ця властивість невірна.

Властивість 4. Добуток обмеженої функції на нескінченно велику при є функцією нескінченно великою при . Наприклад, функція є нескінченно великою при , оскільки функція обмежена.

Наслідок. Добуток сталої на нескінченно велику при функцію є функцією нескінченно великою при .

Властивість 5. Функція, обернена за величиною до нескінченно великої при є нескінченно малою при , і навпаки.

Якщо прийняти символом нескінченно малої функції 0, символом нескінченно великої , то усі викладені властивості можна записати так:

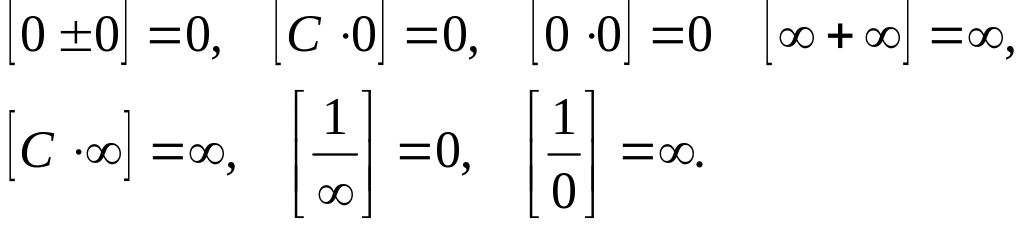
Квадратні дужки вказують на символіку представлених записів.