9. Вопросы и упражнения для самостоятельной работы

1. Каково необходимое и достаточное условие того, чтобы многочлен делился на в кольце K[x]?

2. Для чего служит схема Горнера?

3. Докажите, что если - различные корни многочлена , то делится на .

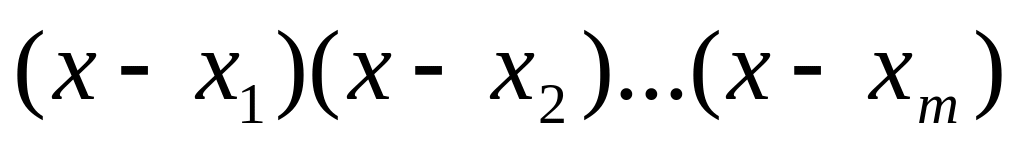4. Какое максимальное число корней может иметь ненулевой многочлен степени n?

5. Что такое евклидово кольцо?

6. Почему кольцо многочленов над любым полем является евклидовым кольцом?

7. Докажите единственность деления с остатком в кольце многочленов.

8. Какие многочлены являются ассоциированными элементами кольца P[x]?

9. Что такое НОД многочленов ?

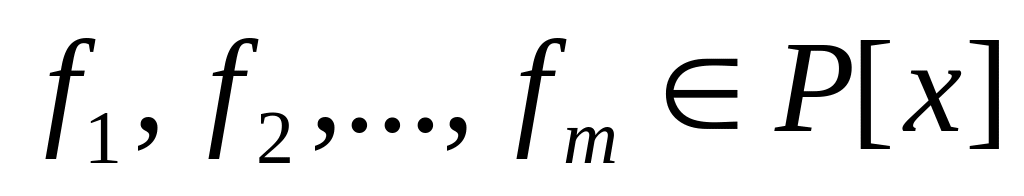10. Что такое взаимно простые многочлены?

11. В чем состоит критерий взаимной простоты многочленов ?

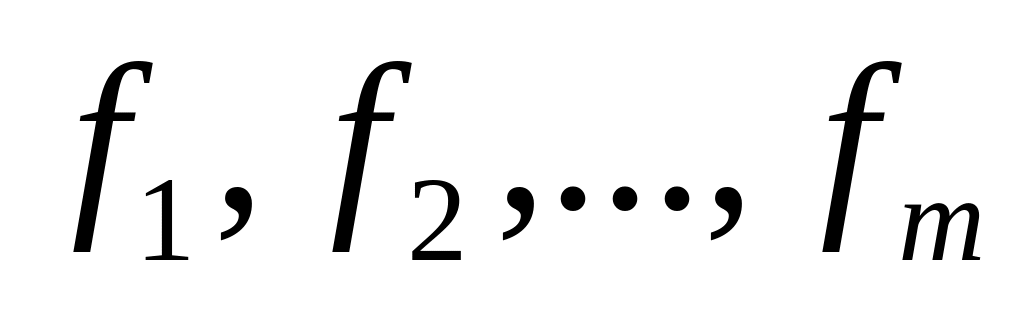12. Для чего служит алгоритм Евклида?

13. Как найти наибольший общий делитель трех многочленов?

14. Что такое наименьшее общее кратное нескольких многочленов?

15. Как связаны НОК и НОД двух многочленов?

Лекция 9 Алгебраическая замкнутость поля

Комплексных чисел

1. Вводное замечание.

2. Свойства модуля многочлена.

3. Основная теорема алгебры комплексных чисел.

4. Разложение многочлена над полем С в произведение линейных множителей.

5. Разложение многочлена над полем R в произведение неприводимых множителей.

6. Задачи и упражнения для самостоятельного выполнения.

1. Вводные замечания

Будем теперь изучать специальные свойства многочленов с числовыми коэффициентами, т.е. многочленов над числовыми полями. Важность этого вопроса обусловлена тем, что многие задачи в разных областях математики, техники, естествознания, экономики сводятся к решению и исследованию алгебраических уравнений или их систем с действительными или комплексными коэффициентами.

В связи с этим именно теория многочленов с числовыми коэффициентами была до середины 19 века основным предметом алгебры; на ее основе возникли и развились современные взгляды на кольца, поля и другие алгебраические структуры и на многочлены над абстрактными полями.

Особое значение имеет изучение свойств многочленов над числовыми полями для учителей, т.к. в школе рассматриваются только такие многочлены и соответствующие им алгебраические уравнения.

Как было показано ранее, для многочленов над числовыми полями алгебраическая и функциональная трактовки равноправны. Это значит, что такие многочлены можно рассматривать как функции действительной и комплексной переменной и применять к ним понятия и утверждения, установленные для таких функций, в частности, понятия и свойства непрерывных функций. Поэтому мы в этой теме будем придерживаться функциональной трактовки многочлена, поскольку она используется при рассмотрении существования и исследования числа корней многочлена числовыми коэффициентами, а также соответствует как историческому развитию алгебры, так и содержанию школьной программы по математике.

До сего момента мы изучали в основном те свойства многочленов, которые не зависели от того, какому полю принадлежали их коэффициенты, т.е. мы рассматривали те свойства многочленов, которые были общими для разных полей и допускали общее доказательство. Например, разложение многочлена на неприводимые множители не является одинаковыми над разными полями, мы рассматривали общее свойство этих разложений, заключающиеся в том, что над производным полем разложения возможно и единственно для данного поля. Общими для всех полей Р являются также свойства операций в кольце многочленов , основные факты теории делимости многочленов, свойства симметрических многочленов и т.д. Очевидно, что все эти свойства имеют место и для многочленов над произвольным числовым полем.

Важными характеристиками многочлена являются наличие и число его корней. Но эти характеристики многочлена уже зависят от выбора поля Р, которому принадлежат коэффициенты многочлена. Ведь один и тот же многочлен может иметь корни в одном поле и не иметь их в другом поле. Например, многочлен не имеет корней в поле R действительных чисел, но имеет два корня в виде С комплексных чисел.

Как было установлено, для каждого многочлена из кольца существует поле разложения, а именно такое расширение Р₁ поля Р, над которым многочлен разлагается в произведение линейных множителей. Среди числовых полей наиболее важную особенность имеет поле С. Оказывается, что полем разложения всякого многочлена над полем С является само поле С, т.е. в поле комплексных чисел всякий многочлен разлагается в произведение линейных множителей.

Этот факт в алгебре формулируется так: поле С алгебраически замкнуто. Как мы видели, поле R действительных чисел этой фундаментальной особенностью не обладает.

В связи с этим изучение свойств многочленов с комплексными коэффициентами, или иначе – целых рациональных функций комплексного переменного, является особенно важной задачей.