Группы и подгруппы

1. Группы.

2. Группа подстановок.

3. Подгруппы.

4. Циклические группы.

5. Разложение группы на подгруппы.

1. Группы

Алгебраическую операцию, определенную в группе, называют умножением или сложением. Группу относительно операции умножения называют мультипликативной, а относительно операции сложения – аддитивной.

Условимся, как это принято в общей теории групп, рассматривать дальше в основном мультипликативные группы.

Пусть G – непустое множество, в котором определена операция умножения.

Определение 1. Непустое множество G, в котором определена операция умножения, называется группой, если выполняются следующие условия:

1. Операция умножения ассоциативна.

2. В множестве G существует единичный элемент.

3. Для каждого элемента 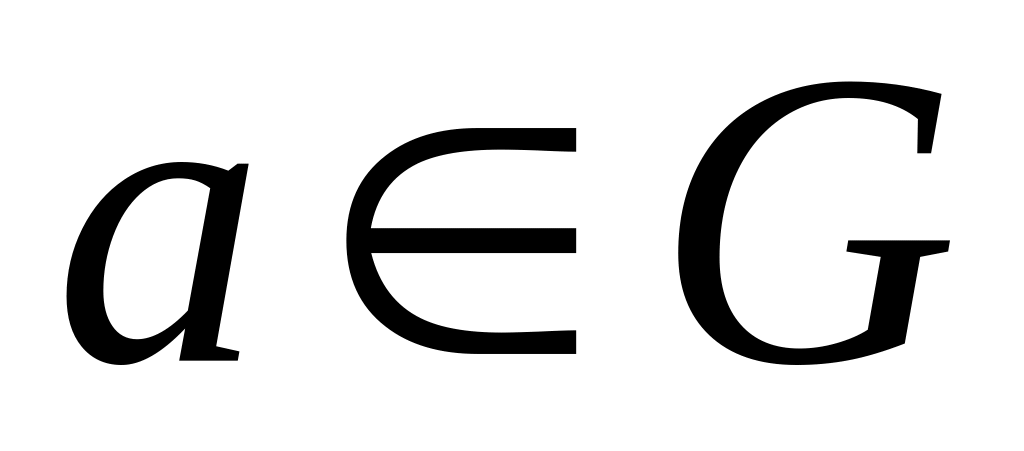в множестве G существует обратный элемент а^-1.

Если операция умножения, определена в группе, коммутативна, то группа G называется коммутативной или абелевой.

Группа G называется конечной, если множество ее элементов конечно; она называется бесконечной, если множество ее элементов бесконечно. Число элементов группы называют порядком группы.

Из определения группы вытекают следующие следствия.

1. В каждой мультипликативной группе можно выполнять левосторонние и правосторонние сокращения: если ав₁=ав₂ или в₁а=ва, то в₁=в₂.

2. Какие бы ни были целые числа m и n, для которого элемента а мультипликативной группы G справедливы равенства

3. Для операции умножения в множестве G выполняется обратная операция – деление, т.е. для любых элементов множества G каждое из уравнений ах=b и ya=b имеет в множестве G решение и притом только одно.

4. Единичный элемент е мультипликативной группы G единственный.

5. В каждой мультипликативной группе G для любого ее элемента а существует единственный обратный ему элемент а^-1, т.е. такой, что

Примерами мультипликативной группы являются множество всех положительных рациональных чисел, всех отличных от нуля рациональных чисел, множество всех положительных действительных чисел, всех отличных от нуля действительных чисел, множество всех отличных от нуля комплексных чисел. Все эти группы – бесконечные, абелевы. Примером мультипликативной бесконечной некоммутативной группы является множество невырожденных матриц n-го порядка над полем комплексных чисел С. Множество всех комплексных корней n-й степени из 1 является мультипликативной абелевой группой порядка n.

2. Группа подстановок

Важными примерами конечных некоммутативных групп являются группы подстановок. Вспомним некоторые сведения о перестановках из n элементов. Пусть дано некоторое множество М, которое состоит из n элементов. Элементы этого множества можно перенумеровать с помощью чисел 1, 2, 3,…, n. Индивидуальные свойства элементов множества М дальше не будут играть никакой роли, поэтому мы просто будем считать, что множество М состоит из чисел 1,2,3,…,n.

Всякое расположение чисел 1,2,3,…,n в некотором определенном порядке называется перестановкой из n чисел или из n элементов.

Число разложенных перестановок из n элементов равно Принято считать, что в перестановке элементы и образуют инверсию, если но стоит в перестановке левее .

Перестановку, элементы которой образуют четное число инверсий, называют четной, а перестановку, элементы которой образуют нечетное число инверсий, называют нечетной.

Преобразование перестановки, при котором некоторые два элемента меняются местами, а остальные остаются на своих местах, называют транспозицией.

Как известно каждая транспозиция меняет четность перестановки.

Пусть А₁ и А₂ – две различные перестановки из символов 1,2,…,n. Если мы выполним в обеих этих перестановках транспозицию любых двух, но одних и тех же символов, то получим две различные перестановки и . Действительно, если бы перестановки и были одинаковы, то были бы одинаковыми и перестановки А₁ и А₂, т.к. их получают из и с помощью обратной транспозиции тех же самых символов.

Теорема 1. При n 2 число четных перестановок из n элементов равно числу нечетных и равно

Действительно, выполним во всех n! перестановках из n элементов транспозицию двух одних и тех же элементов.

В результате получаем и n! различных перестановок, т.е. все n! перестановок из n элементов. Но при этом все четные перестановки переходят в нечетные, а нечетные – в четные. Следовательно, число четных перестановок равно числу нечетных и равно

Известно также, что от каждой перестановки из n элементов можно перейти к произвольной другой перестановке из этих же элементов с помощью некоторых транспозиций.

Определение 2. Всякое взаимно однозначное отображение множества самое на себя называется подстановкой из n элементов или подстановкой n-й степени.

Подстановки будем обозначать большими буквами латинского алфавита: А,В,С и др.

Если при перестановке А число i (i=1,2,…,n) отображается в число , то записывают

(1)

т.е. под каждым из чисел 1,2,3,…,n записывают то число, в которое оно отображается, и полученные две строчки берут в скобки.

Запись (1) надо читать так: при подстановке А переходит в , 2 переходит в , …, n переходит в . Т.к. перестановка является биективным отображением, то все числа различные и, следовательно, вторая строчка в записи (1) представляет собой перестановку из элементов 1,2,…,n. Значит, каждую подстановку n-й степени можно записать с помощью двух подстановок из чисел 1,2,…,n, записанных одна под другой:

.

Теорема 2. Число подстановок n-й степени равно n!

□ Действительно, запишем поочередно под постановкой 1,2,…,n каждую перестановку из чисел 1,2,…,n, тогда получим все возможные различные подстановки n-й степени. Так число всех подстановок из n элементов равно n!, то и число всех подстановок n-й степени равно n! ■

Определение 3. Подстановка А называется четной, если четности верхней и нижней перестановок ее и записи совпадают; она называется нечетной, если четности этих перестановок различны. Равносильным этому является следующее определение.

Определение 4. Подстановка А называется четной, если суммарное число инверсий в верхней и нижней перестановках ее записи четное, в противном случае называется нечетной.

Теорема 3. При число четных подстановок n-й степени равно числу нечетных, т.е. равно

□ Действительно, подпишем поочередно под перестановкой 1,2,…,n каждую из четных перестановок, получим четных подстановок, а подписав под перестановкой 1,2,…,n каждую нечетную перестановку, получим нечетных перестановок. ■

Пример 1. Определим четность подстановки 6-й степени

В верхней перестановке 5 инверсий, а в нижней 11. Общее число инверсий 16. Значит, подстановка А – четная.

Запишем теперь эту подстановку так:

В верхней перестановке этой записи 0 инверсий, а в нижней – 8. Общее число их – 8. Этот пример показывает, что при различных записей данной подстановки четность общее число инверсий в обеих перестановках ее записи сохраняется, а само число инверсий, вообще говоря, изменяется.

Возьмем две произвольные подстановки n-й степени

и

Выполним последовательности подстановки А и В. В результате получим подстановку

Определение 4. Подстановка С, которая является результатом последовательного выполнения подстановок А и В, называется произведением подстановки А на подстановку В и записывается С=АВ.

Пример. Пусть

, , то

Действительно, подстановка А отображает 1 в 2, а подстановка В отображает 2 в 4. Следовательно, АВ отображает 1 в 4. Аналогично отображаются и другие элементы.

Операция умножения подстановок n-й степени при некоммутативна. Действительно, для подстановок

, ,

т.к. подстановка АВ отображает 1 в 2, а подстановка ВА отображает 1 в 1.

Операция умножения подстановок ассоциативна.

Действительно, пусть даны подстановки n-й степени А, В и С. Предположим, что произвольно выбранный элемент k ( ) при подстановке А переходит при подстановке В переходит в b_k, а b_k при подстановке С переходит в с_k. Тогда при подстановке АВ элемент k переходит в b_k, а при подстановке (АВ)С элемент переходит в С_k. Рассмотрим теперь подстановку А(ВС). При подстановке А элемент k переходит в элемент а_k, при подстановке ВС элемент а_k перейдет в С_k, поэтому при подстановке А(ВС) элемент k также перейдет в С_k. Следовательно, (АВ)С=А(ВС).

Теорема 4. Множество всех подстановок n-й степени является группой по умножению.

□ Действительно, операция умножения подстановок ассоциативна. Среди подстановок n-й степени есть подстановка , при которой каждый элемент отображается сам в себя, эту подстановку называют тождественной. Очевидно, что для любой подстановки А: , т.е. подстановка Е играет роль единичного элемента. Для каждой подстановки n-й степени существует подстановка А^-1= такая, что .■ Подстановку А^-1 называют обратной для А.

Следовательно, множество подстановок n-й степени, по определению 1, является группой.

Группу всех подстановок n-й степени называют симметрической группой n-й степени и обозначают S_n. Порядок группы S_n равен n!

Рассмотрим теперь подстановку вида

(2)

Элементы, которые остаются неподвижными, заменим точками и запишем эту подстановку сокращенно

(3)

Очевидно, что подстановку (3) можно получить из тождественной подстановки с помощью выполнения транспозиций i и j в нижней подстановке. На основе этого подстановки вида (3) тоже называют транспозициями и обобщают (i, j).