
- •Алгебра
- •График учебного процесса
- •III семестр
- •IV семестр
- •1. Цели и задачи дисциплины, место в учебном процессе, требования к уровню содержания дисциплины.
- •2. Технологическая карта дисциплины
- •3. Содержание дисциплины
- •Самостоятельная работа (темы , выносимые на срс и методическая поддержка срс)
- •Литература для самостоятельной работы
- •4. Организация текущего и промежуточного контроля знаний
- •5. Методические рекомендации преподавателю
- •6. Работа с ресурсами Internet
- •7. Материальное обеспечение дисциплины
- •8. Методическое обеспечение дисциплины:
- •Глоссарий
- •Вопросы, выносимые на экзамены
- •III семестр
- •IV семестр
- •Методические рекомендации по организации внеаудиторной и аудиторной самостоятельной работы студентов
- •Контрольно - измерительные материалы
- •III семестр Модуль 1
- •Модуль 2 Контрольная работа по теме «Многочлены от одной переменной»
- •IV семестр Модуль 1 Тест по теме «Многочлены над полем рациональных чисел» для межсессионного учета знаний
- •Контрольная работа по теме «Многочлены над полями рациональных, действительных и комплексных чисел»
- •Модуль 2 Контрольная работа по теме «Расширения полей и задачи, связанные с этим»
- •Методические указания по подготовке практических занятий
- •Методические рекомендации по выполнению курсовых работ
- •Темы курсовых работ
- •1. Вопросы делимости и решения уравнений в кольце целых чисел.
- •. Программа итоговой государственной аттестации студентов
- •Группы и подгруппы
- •Группа подстановок
- •Подгруппы
- •Циклические группы
- •Разложение группы по подгруппе
- •6. Задачи и упражнения для самостоятельного выполнения
- •Нормальные делители. Фактор - группы.
- •1. Нормальные делители
- •2. Фактор – группы
- •Гомоморфизмы групп
- •Задачи и упражнения для самостоятельного выполнения
- •Элементарные сведения о кольцах
- •Кольцо с единицей
- •Делители нуля. Область целостности
- •Поле частных
- •Задачи и упражнения для самостоятельного выполнения
- •Гомоморфизмы колец
- •Понятие идеала. Примеры
- •Операции над идеалами
- •Сравнения и классы вычетов по идеалу. Фактор – кольцо
- •Гомоморфизм колец. Теорема о гомоморфизмах
- •Характеристика кольца с единицей
- •Задачи и упражнения для самостоятельного выполнения
- •Делимость в области целостности
- •2. Кольцо главных идеалов
- •Евклидовы кольца.
- •Задачи и упражнения для самостоятельного выполнения
- •1. Многочлены над полем
- •2. Кольцо многочленов как евклидово кольцо
- •3. Техника деления с остатком. Схема Горнера
- •4. Теорема Безу
- •5. Наибольший общий делитель. Алгоритм Евклида
- •6.Наименьшее общее кратное
- •7. Неприводимые многочлены
- •8. Каноническое разложение многочлена
- •9. Вопросы и упражнения для самостоятельной работы
- •Комплексных чисел
- •1. Вводные замечания
- •2. Свойства модуля многочлена
- •3. Основная теорема алгебры комплексных чисел
- •4. Разложение многочлена над полем с в произведение линейных множителей
- •5. Разложение многочленов над полем r в произведение неприводимых множителей
- •6 Задачи и упражнения для самостоятельного выполнения
- •IV семестр
- •Приводимость и неприводимость многочленов над полем действительных, комплексных и рациональных чисел
- •Рациональные корни многочлена с рациональными коэффициентами
- •Понятие алгебраического числа
- •1. Вводные замечания
- •2. Свойства модуля многочлена
- •3. Основная теорема алгебры комплексных чисел
- •4. Разложение многочлена над полем с
- •5. Разложение многочленов над полем r
- •6 Задачи и упражнения для самостоятельного выполнения
- •1. Алгебраические числа.
- •2. Простое алгебраическое расширение поля.
- •3. Уничтожение иррациональности в знаменателе.
- •4. Конечные расширения полей.
- •6. Вопросы и упражнения для самостоятельной работы.
- •Лекции 7-8
- •Поле алгебраических чисел
- •Понятие разрешимости в квадратных радикалах
- •Определение 1. Алгебраическое уравнение
- •Связь с расширением числовых полей
- •4. Признаки того, что число выражается в квадратных радикалах.
- •5. Общий критерий разрешимости в квадратных радикалах
- •6. Примеры геометрических задач, сводящихся к уравнениям, неразрешимым в квадратных радикалах
- •Задача об удвоении куба
- •Задача о трисекции угла
- •Задача о квадратуре круга
- •7. Вопросы и упражнения для самостоятельной работы
4. Теорема Безу
Теорема 1 (Безу). Для любого элемента из поля P остаток при делении многочлена f(x) P[x] на равен f( )
Доказательство:
Деля f(x)
на
с
остатком, имеем
![]() ,
где многочлен
есть константа, поскольку его степень
меньше степени
,
где многочлен
есть константа, поскольку его степень
меньше степени
В это равенство
вместо
![]() подставим
,
получим f(
)=(
-
)
S(
)
+
;
f(
)
=
.
И в алгебре, и в математическом анализе
часто приходится разлагать многочлен
f(x) по
степеням
подставим
,
получим f(
)=(
-
)
S(
)
+
;
f(
)
=
.
И в алгебре, и в математическом анализе
часто приходится разлагать многочлен
f(x) по
степеням
![]()
Пусть многочлен
f(x)
– многочлен n-ой
степени над полем P;
- элемент этого поля. Деление многочлена
f(x)
на
даёт
нам: f(x)=(
)
f1(x)
+
![]() ,
где f1(x)
– многочлен (n-1)-й
степени, а
,
где f1(x)
– многочлен (n-1)-й
степени, а
![]() - элемент поля P. Если
n > 1, то поделим
f1(x)
на
:
- элемент поля P. Если
n > 1, то поделим
f1(x)
на
:
f1(x)
= (
)f2(x)+![]() ,
где степень f2(x)
равна (n – 2).
Аналогично получаем
,
где степень f2(x)
равна (n – 2).
Аналогично получаем
………………………
fn-1(x)
=
![]() fn(x)+
fn(x)+![]() .
Очевидно, что степень fn(x)=0
т.е. fn(x)
=
.
Очевидно, что степень fn(x)=0
т.е. fn(x)
=
![]() - констант, элемент поля P.
Выразим
из этих равенств: f(x)=
- констант, элемент поля P.
Выразим
из этих равенств: f(x)=![]() . Такое выражение многочлена f(x)
называется разложением его по степеням
двучлена
.
При этом коэффициенты
. Такое выражение многочлена f(x)
называется разложением его по степеням
двучлена
.
При этом коэффициенты
![]() - есть остатки от деления многочлена :
- остаток от деления f(x)
на
,
- есть остатки от деления многочлена :
- остаток от деления f(x)
на
,
![]() - остаток от деления f1(x)
на
,
…,
- остаток от деления
- остаток от деления f1(x)
на
,
…,
- остаток от деления
![]() на
,
- последнее частное в процессе
последовательного деления.
на
,
- последнее частное в процессе
последовательного деления.
Пример 5.
Найти разложение многочлена f(x)=![]() по степеням двучлена
по степеням двучлена
![]()
Составим следующую таблицу, пользуясь схемой Горнера
|
1 |
0 |
-3 |
1 |
-2 |
1 |
1 |
1 |
1 |
-2 |
-1 |
-3 |
|
1 |
1 |
2 |
0 |
-1 |
|
|
1 |
1 |
3 |
3 |
|
|
|
1 |
1 |
4 |
7 |
|
|
|
1 |
1 |
5 |
|
|
|
|
1 |
|
|
|
|
|
|
В первой строке
этой таблицы стоят коэффициенты данного
многочлена, во второй строке – коэффициенты
частного
![]() и остатка
и остатка
![]() ,
в третьей строке содержится результат
деления
на
и остаток
,
в третьей строке содержится результат
деления
на
и остаток
![]() и т.д. Искомыми коэффициентам являются
обведенные в таблице числа
и т.д. Искомыми коэффициентам являются
обведенные в таблице числа
![]() ,
а разложение f(x)
по степеням
имеет вид:
,
а разложение f(x)
по степеням
имеет вид:
f(x)
=
![]()
Пример 6. Разложить на простейшие дроби дробь:
![]() Для
этого разложим числитель дроби, т.е.
многочлен
Для
этого разложим числитель дроби, т.е.
многочлен
![]() по степеням двучлена
по степеням двучлена
![]() ,
который находится в знаменателе дроби.
Опять применим Схему Горнеру, получим:
,
который находится в знаменателе дроби.
Опять применим Схему Горнеру, получим:
|
1 |
0 |
2 |
-3 |
-3 |
1 |
-3 |
11 |
- 36 |
-3 |
1 |
-6 |
29 |
|
-3 |
1 |
|
|
|
-3 |
|
|
|
|
Следовательно
![]() .
И поделим почленно числитель полученной
дроби на знаменатель, получим:
.
И поделим почленно числитель полученной
дроби на знаменатель, получим:
![]() -
Это и есть разложение данной дроби на
простейшие дроби.
-
Это и есть разложение данной дроби на
простейшие дроби.

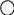 -2
-2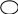 -4
-4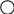 2
2 1
1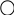 -9
-9 1
1