2. Кольцо с единицей

Из определения кольца не вытекает существование или отсутствие в нем единицы е. Но, как было доказано в алгебре на I курсе, если в кольце К единичный элемент существует, то только один. В нулевом кольце , состоящем только из одного нуля, элемент 0 одновременно является и единицей, т.к. .

Определение. Нулевое кольцо К, в котором есть единичный элемент е, называется кольцом с единицей.

Примерами колец с единицей являются: кольцо целых чисел Z; кольцо рациональных чисел Q; кольцо действительных чисел R; кольцо комплексных чисел С; кольцо матриц n-го порядка над полями R, Q, C, единицей этих колец является матрица

Примерами кольца, в котором нет единицы, служит кольцо целых чисел, кратных произвольно выбранному натуральному числу m>1; в частности, нет единицы в кольце четных целых чисел.

Пусть К – произвольное кольцо с единицей е. Для всякого отличного от нуля элемента а К справедливы равенства

Отсюда следует, что .

Если для элемента а К в кольце К существует обратный элемент а^-1, то только один. Элемент е является обратным для самого себя. Из равенства следует, что элемент – е также является обратным для самого себя. Элемент 0 не имеет обратного элемента, т.к. для любого а К. Если для а К в кольце К существует обратный элемент а^-1, то а , по определению делителей элемента кольца, является делителем e, т.к. .

Поэтому можно принять такое определение.

Определение 2. Элемент а, для которого в кольце К существует обратный элемент а^-1, называется обратимым или делителем единицы.

Пример. Кольцо Z является самым простым примером коммутативного кольца, в котором только 1 и -1 являются делителями единицы.

Теорема 3. Множество К^* всех делителей единицы кольца К является группой по умножению.

□ Пусть элементы , т.е. являются делителями единицы е. Значит и , а это значит, что а^-1 и ab тоже являются делителями е, а, значит, содержатся в К^*, е также содержится в К^*. Поэтому К^* является мультипликативной группой.

Группа К^* называется группой делителей единичного элемента, или группой обратимых элементов кольца К.■

3. Делители нуля. Область целостности

Пусть К – произвольное кольцо. Для выполняется равенство . Следовательно, каждый элемент кольца является делителем нуля. Но в теории колец принимают следующее определение делителей нуля.

Определение 3. Элементы а и b кольца К называются делителями нуля, если и , но ab=0, при этом а называется левым, а b – правым делителем нуля.

В коммутативных кольцах очевидно, что понятия левого и правого делителей нуля совпадают.

Пример 1. В качестве кольца К рассмотрим кольцо классов вычетов Z_m, где m – некоторое составное целое число, например, . Тогда классы вычетов и отличные от нулевого класса , а их произведение равно нулевому классу: . Следовательно, классы и являются делителями нуля в кольце Z_m.

Пример 2. В кольце R_n матриц n-го порядка ( ) с действительными элементами матрицы

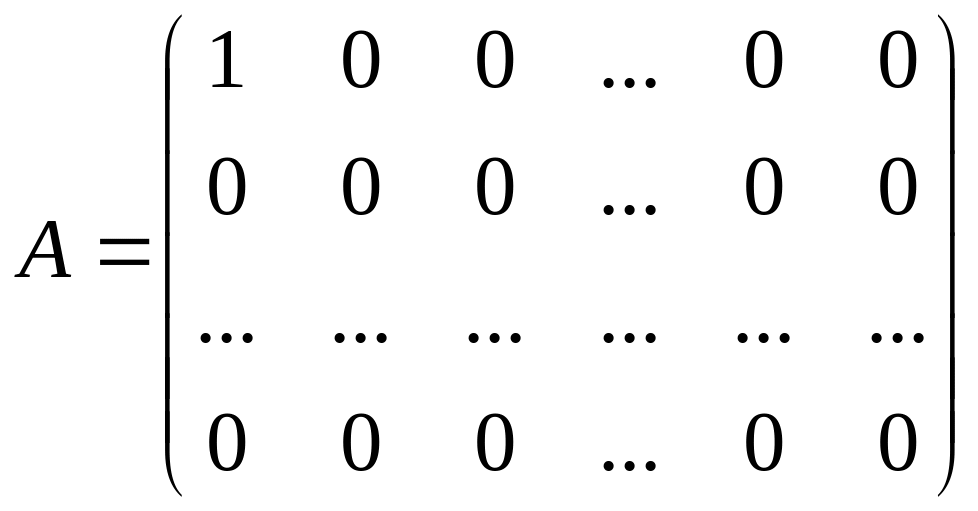и

являются делителями в кольце R_n.

Определение 4. Коммутативное кольцо с единицей, в котором нет делителей нуля, называется областью целостности.

Пример 1. Очевидно, что всякое числовое кольцо является областью целостности.

Пример 2. Областью целостности является всякое поле Р, т.к. .