
- •Алгебра
- •График учебного процесса
- •III семестр
- •IV семестр
- •1. Цели и задачи дисциплины, место в учебном процессе, требования к уровню содержания дисциплины.
- •2. Технологическая карта дисциплины
- •3. Содержание дисциплины
- •Самостоятельная работа (темы , выносимые на срс и методическая поддержка срс)
- •Литература для самостоятельной работы
- •4. Организация текущего и промежуточного контроля знаний
- •5. Методические рекомендации преподавателю
- •6. Работа с ресурсами Internet
- •7. Материальное обеспечение дисциплины
- •8. Методическое обеспечение дисциплины:
- •Глоссарий
- •Вопросы, выносимые на экзамены
- •III семестр
- •IV семестр
- •Методические рекомендации по организации внеаудиторной и аудиторной самостоятельной работы студентов
- •Контрольно - измерительные материалы
- •III семестр Модуль 1
- •Модуль 2 Контрольная работа по теме «Многочлены от одной переменной»
- •IV семестр Модуль 1 Тест по теме «Многочлены над полем рациональных чисел» для межсессионного учета знаний
- •Контрольная работа по теме «Многочлены над полями рациональных, действительных и комплексных чисел»
- •Модуль 2 Контрольная работа по теме «Расширения полей и задачи, связанные с этим»
- •Методические указания по подготовке практических занятий
- •Методические рекомендации по выполнению курсовых работ
- •Темы курсовых работ
- •1. Вопросы делимости и решения уравнений в кольце целых чисел.
- •. Программа итоговой государственной аттестации студентов
- •Группы и подгруппы
- •Группа подстановок
- •Подгруппы
- •Циклические группы
- •Разложение группы по подгруппе
- •6. Задачи и упражнения для самостоятельного выполнения
- •Нормальные делители. Фактор - группы.
- •1. Нормальные делители
- •2. Фактор – группы
- •Гомоморфизмы групп
- •Задачи и упражнения для самостоятельного выполнения
- •Элементарные сведения о кольцах
- •Кольцо с единицей
- •Делители нуля. Область целостности
- •Поле частных
- •Задачи и упражнения для самостоятельного выполнения
- •Гомоморфизмы колец
- •Понятие идеала. Примеры
- •Операции над идеалами
- •Сравнения и классы вычетов по идеалу. Фактор – кольцо
- •Гомоморфизм колец. Теорема о гомоморфизмах
- •Характеристика кольца с единицей
- •Задачи и упражнения для самостоятельного выполнения
- •Делимость в области целостности
- •2. Кольцо главных идеалов
- •Евклидовы кольца.
- •Задачи и упражнения для самостоятельного выполнения
- •1. Многочлены над полем
- •2. Кольцо многочленов как евклидово кольцо
- •3. Техника деления с остатком. Схема Горнера
- •4. Теорема Безу
- •5. Наибольший общий делитель. Алгоритм Евклида
- •6.Наименьшее общее кратное
- •7. Неприводимые многочлены
- •8. Каноническое разложение многочлена
- •9. Вопросы и упражнения для самостоятельной работы
- •Комплексных чисел
- •1. Вводные замечания
- •2. Свойства модуля многочлена
- •3. Основная теорема алгебры комплексных чисел
- •4. Разложение многочлена над полем с в произведение линейных множителей
- •5. Разложение многочленов над полем r в произведение неприводимых множителей
- •6 Задачи и упражнения для самостоятельного выполнения
- •IV семестр
- •Приводимость и неприводимость многочленов над полем действительных, комплексных и рациональных чисел
- •Рациональные корни многочлена с рациональными коэффициентами
- •Понятие алгебраического числа
- •1. Вводные замечания
- •2. Свойства модуля многочлена
- •3. Основная теорема алгебры комплексных чисел
- •4. Разложение многочлена над полем с
- •5. Разложение многочленов над полем r
- •6 Задачи и упражнения для самостоятельного выполнения
- •1. Алгебраические числа.
- •2. Простое алгебраическое расширение поля.
- •3. Уничтожение иррациональности в знаменателе.
- •4. Конечные расширения полей.
- •6. Вопросы и упражнения для самостоятельной работы.
- •Лекции 7-8
- •Поле алгебраических чисел
- •Понятие разрешимости в квадратных радикалах
- •Определение 1. Алгебраическое уравнение
- •Связь с расширением числовых полей
- •4. Признаки того, что число выражается в квадратных радикалах.
- •5. Общий критерий разрешимости в квадратных радикалах
- •6. Примеры геометрических задач, сводящихся к уравнениям, неразрешимым в квадратных радикалах
- •Задача об удвоении куба
- •Задача о трисекции угла
- •Задача о квадратуре круга
- •7. Вопросы и упражнения для самостоятельной работы
Гомоморфизмы групп
Определение 1. Гомоморфизмом, или гомоморфным отображением группы G в группу G/ , которые удовлетворяют условию
![]() (4)
(4)
Если группа G и G/ аддитивные, то условие гомоморфизма (4) записывается так:
![]()
Пример
1. Пусть Sn
– симметрическая группа n-й
степени и G={1,-1}
– мультипликативная группа, состоящая
из чисел 1 и -1. Рассмотрим отношение
![]() группы Sn
на G,
которое задается так: для каждой
подстановки A
Sn
группы Sn
на G,
которое задается так: для каждой
подстановки A
Sn
![]() если А
– четная подстановка,
если А
– четная подстановка,
![]() если А
– нечетная подстановка.
если А
– нечетная подстановка.
Очевидно,
что
– отображение группы Sn
на группу G,
причем выполняется условие
![]() .
Значит
гомоморфизм группы Sn
на группу
G
.
.
Значит
гомоморфизм группы Sn
на группу
G
.
Пример
2. Пусть
– группа невырожденных матриц порядка
n
над полем действительных чисел R;
![]() – мультипликативная группа отличных
от нуля действительных чисел. Пусть ψ
– отображение
– мультипликативная группа отличных
от нуля действительных чисел. Пусть ψ
– отображение
![]() в
группе
,
которое каждой матрице А
ставит в соответствие ее определитель
в
группе
,
которое каждой матрице А
ставит в соответствие ее определитель
![]() .
Для произвольного числа
.
Для произвольного числа
![]() существует такая матрица
существует такая матрица
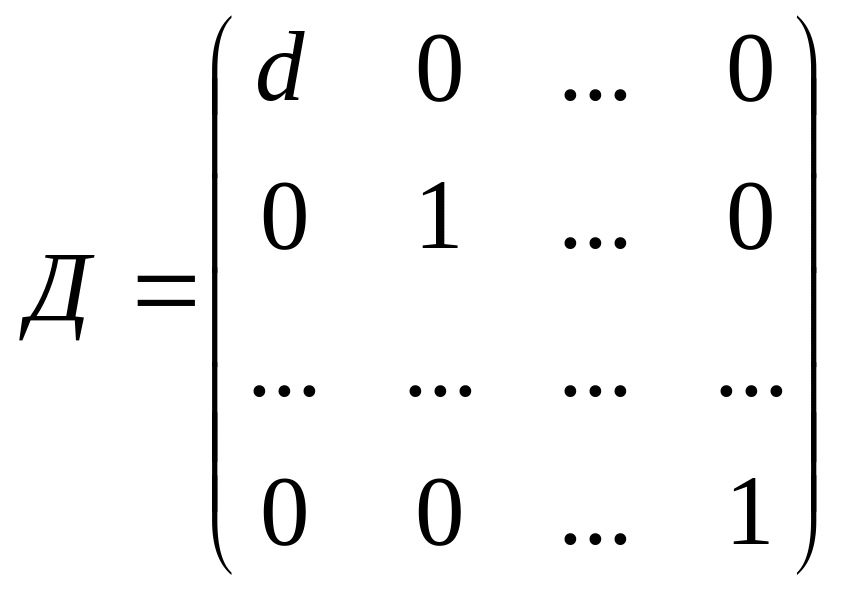 ,
что
,
что
![]() .
.
Следовательно,
ψ
–однозначное отображение группы Rn
на группу R*.
А так как
![]() ,
то ψ
– гомоморфизме
на
.
,
то ψ
– гомоморфизме
на
.
Пример
3. Пусть G
– некоторая группа, Н
– любой ее нормальный делитель. Пусть
χ–
отображение, которое каждому элементу
g
G
ставит в соответствии смежный класс gH
группы G
по нормальному делителю Н,
в котором содержится этот элемент.
Очевидно, что χ
является
отображение группы G
на фактор – группу G/H:
следует,
![]() что
что
![]() .
.
Следовательно, χ – гомоморфное отображение G на G/H. Этот гомоморфизм χ называется естественным или каноническим гомоморфизмом группы G на фактор – группу G/H.
Докажем несколько теорем, которые характеризуют гомоморфные отображения групп.
Теорема 7. При гомоморфном отображении φ группы G в группу G/ единичный элемент е группы G отображается в единичный элемент е/ группы G/.
□ Из
равенства ее=е
следует, что
![]() С другой стороны,
С другой стороны,
![]() Следовательно,
Следовательно,
![]() ,
а отсюда
,
а отсюда
![]() ■
■
Теорема 8. Если φ – гомоморфизм группы G на группу G/, то
![]()
□ Действительно,
![]() .
Отсюда
.
Отсюда
![]() .■
.■
Теорема 9. Если φ является гомоморфизмом группы G в группу G/. То φ(G) является подгруппой группы G/.
□ Пусть
a/
и b/
– любые элементы из множества G/.
Тогда
![]() где
где
![]() и
и
![]() ■
■
Определение
2. Пусть φ
является гомоморфным отображением
группы G
в группу G/.
Следовательно К
всех элементов группы G,
которые при гомоморфизме φ
отображаются в единицу е/
группы G,
называется ядром гомоморфизма
и записывается
![]() .
.
Теорема 10. Ядро всякого гомоморфизма φ группы G является нормальным делителем группы G.
□ Если
![]() ,
то
,
то
![]() ,
так как
,
так как
![]() ,
если
,
если
![]() ,
т.е.
,
т.е.
![]() ,
то и
,
то и
![]() ,
ибо
,
ибо
![]() .
Следовательно,
.
Следовательно,
![]() является подгруппой группы G/.
Пусть теперь а
– произвольный элемент ядра
,
a g
– любой элемент группы G.
является подгруппой группы G/.
Пусть теперь а
– произвольный элемент ядра
,
a g
– любой элемент группы G.
Тогда
![]() .
Т.о., подгруппа
вместе с произвольным своим элементом
а содержит и все элементы, сопряженные
с ним в группе G,
и поэтому
является нормальным делителем группы
G.
■
.
Т.о., подгруппа
вместе с произвольным своим элементом
а содержит и все элементы, сопряженные
с ним в группе G,
и поэтому
является нормальным делителем группы
G.
■
Пример
1. Пусть χ
– естественный гомоморфизм произвольной
группы G
на некоторую ее фактор – группу G/H
то нормальному делителю Н.
Тогда
![]() .
.
Теорема 11. (Теорема о гомоморфизмах групп)
Пусть
φ
является гомоморфизмом группы G
на группу G/
и
![]() .
Тогда группа G/
изоморфна
фактор – группе G/H
, причем существует такой изоморфизм ψ
фактор – группы G/H
на группу G/,
что произведение χψ
естественного гомоморфизма
.
Тогда группа G/
изоморфна
фактор – группе G/H
, причем существует такой изоморфизм ψ
фактор – группы G/H
на группу G/,
что произведение χψ
естественного гомоморфизма
![]() на изоморфизм ψ является гомоморфизмом
φ.
на изоморфизм ψ является гомоморфизмом
φ.
□ Пусть
g/
– произвольный элемент группы G/,
а g
такой элемент группы G,
что
![]() .
Т.к. Н
– ядро гомоморфизма φ,
то
.
Т.к. Н
– ядро гомоморфизма φ,
то
![]() поэтому
поэтому
![]() ,
т.е. каждый элемент смежного класса
при гомоморфизме φ
отображается в g/.
C
другой стороны, если
при гомоморфизме φ
отображается в
,
т.е. каждый элемент смежного класса
при гомоморфизме φ
отображается в g/.
C
другой стороны, если
при гомоморфизме φ
отображается в
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() поэтому
поэтому
![]() ,
т.е.
,
т.е.
![]() ,
где
.
Отсюда
,
где
.
Отсюда
![]() .
Т.о., множество всех элементов группы
G,
которые при гомоморфизме φ
отображаются в элемент
,
составляет смежный класс
.
Т.о., множество всех элементов группы
G,
которые при гомоморфизме φ
отображаются в элемент
,
составляет смежный класс
![]() .
.
Обозначим
ψ отображение,
которое каждому смежному классу
![]() ставит в соответствие элемент
,
который при гомоморфизме φ
отображаются
элементы класса
,
т.е.
ставит в соответствие элемент
,
который при гомоморфизме φ
отображаются
элементы класса
,
т.е.
![]() Очевидно, что ψ
является отображением фактор – группы
G/H
на группу G/.
Покажем, что ψ
является изоморфным отображением. Пусть
Очевидно, что ψ
является отображением фактор – группы
G/H
на группу G/.
Покажем, что ψ
является изоморфным отображением. Пусть
![]() и
и
![]() – произвольные элементы из G/H.
Имеем
– произвольные элементы из G/H.
Имеем
![]() Значит, ψ
Значит, ψ![]() ψ
ψ![]() ψ
ψ![]() .
.
Кроме того, отображение ψ взаимно однозначное, т.е.
![]() ψ
ψ![]() ψ
ψ![]() ,
т.к.
,
т.к.
ψ
![]() ψ
ψ![]() .
.
Рассмотрим
теперь отображение χψ.
Поскольку χ
– естественный гомоморфизм группы G
на фактор – группу G/H,
а ψ
– изоморфизм G/H
на G/,
то χφ
– отображение G
на G/.
Докажем, что χψ=φ.
Пусть g
произвольный элемент из G.
По определению естественного гомоморфизма
χ,
![]() и,
по определению изоморфизма ψ,
ψ
и,
по определению изоморфизма ψ,
ψ![]() .
Значит, χψ(g)=ψ
.
Значит, χψ(g)=ψ![]() ψ
,
т.е. χψ
ψ
,
т.е. χψ![]() .
А это означает, что χψ=φ.■
.
А это означает, что χψ=φ.■
Изоморфизмы группы с алгебраической точки зрения, т.е. с точки зрения их свойств, являющихся следствием определенных в них алгебраических операций, а не индивидуальных свойств их элементов, неразличимы.
Следовательно, теорема 11 показывает, что все группы, на которые может гомоморфно отображается группа G, фактически исчерпываются ее фактор – группами, а все гомоморфизмы группы G исчерпываются естественными гомоморфизмами на ее фактор – группы.
