36. Угловой спектр сферической волны

Выражение для комплексной амплитуды сферической волны

Рассмотрим, как разлагается по плоским волнам сферическая волна, комплексная амплитуда которой описывается выражением

,

где .

Такая волна является моделью, описывающей поле точечного источника излучения, и поэтому ее разложение важно для проведения некоторых дальнейших выводов. Уравнение колебаний плоской волны можно получить непосредственно из решения волнового уравнения для точечного источника колебаний.

В плоскости z = 0 распределение комплексных амплитуд будет описываться соотношением

,

где .

Вычисление углового спектра сферической волны

Подставляя выражение в соотношение , можно получить искомый угловой спектр. При этом необходимо вычислить интеграл

,

что можно сделать при помощи замены переменных , , и . После проведения вычислений можно получить, что

.

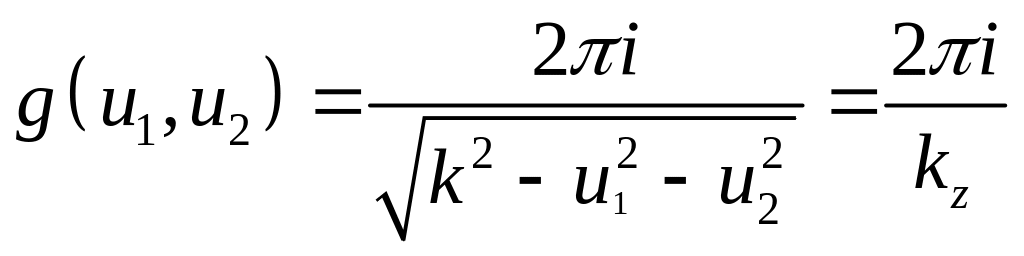Полученное выражение представляет собой угловой спектр сферической волны. Анализируя , можно отметить, что при малых по сравнению с k значениях u₁ и u₂, что соответствует малым углам распространения плоских волн, спектр сферической волны практически постоянен. При увеличении углов распространения и приближении u₁ и u₂ к k спектр начинает возрастать и переходит в область неоднородных волн.

Подставляя выражение для углового спектра в представление Релея , получим искомое разложение:

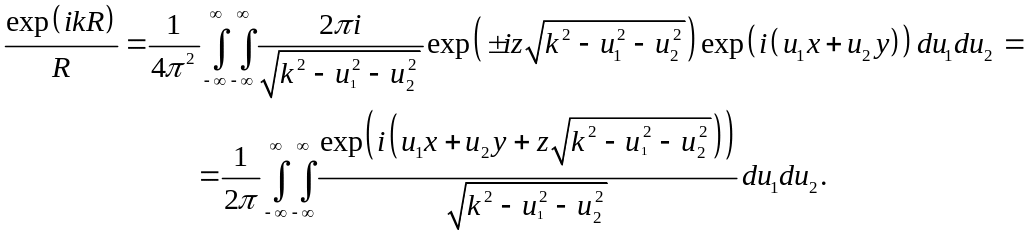
37. Импульсный отклик свободного пространства

Выражение для импульсного отклика свободного пространства

Продолжая аналогию колебательных и волновых систем, выведем выражение для импульсного отклика свободного пространства.

В колебательных системах импульсным откликом называется реакция системы на единичное входное воздействие, или другими словами, импульсный отклик системы – это сигнал на выходе системы при подаче на ее вход бесконечно короткого импульса. В теории линейных систем показано, что импульсный отклик линейной системы и ее частотная характеристика связаны парой преобразований Фурье. Применим это правило к нашей волновой линейной системе и получим выражение для импульсного отклика как обратное преобразование Фурье от уже известной частотной характеристики:

.

Интеграл можно вычислить при помощи соотношения . Дифференцируя по z, получим

.

Сравнивая выражения и , можно получить, что

.

Таким образом, мы получили точное выражение для импульсного отклика свободного пространства.

Физический смысл импульсного отклика свободного пространства заключается в следующем. Представим некоторую монохроматическую волну, распределение комплексной амплитуды поля которой в плоскости z=0 представляет собой единичный импульс (дельта-функцию). Выражение представляет собой распределение комплексной амплитуды этого поля некоторой волны в плоскости z, которое образуется при прохождении этой волной свободного пространства длины z. Следует отметить, что поле такой волны физически нереализуемо.

Аналогично выражению , выражающему распределение комплексной амплитуды поля в некотором сечении через частотную характеристику, можно получить выражение для комплексной амплитуды поля через импульсный отклик свободного пространства:

.

Приближение Френеля. Принцип Гюйгенса-Френеля

Анализируя выражение , можно получить, что для больших (по сравнению с длиной волны) расстояний z импульсная характеристика записывается в виде

при .

Если предположить, что поперечные размеры плоскости, на которой анализируется комплексная амплитуда, также малы по сравнению с расстоянием до этой плоскости, выражение для импульсного отклика еще более упрощается:

при и .

Условия и являются условиями зоны Френеля, таким образом, приближенное выражение для импульсного отклика свободного пространства справедливо в этой зоне.

Вместе с тем можно придти к выводу, что в данном приближении импульсный отклик свободного пространства представляет собой не что иное, как сферическую волну (из сравнения с выражением ). Таким образом, мы приходим к принципу Гюйгенса-Френеля – фронт распространяющейся волны точно такой же, как если бы он был сформирован точечными источниками с амплитудами и фазами колебаний, соответствующими колебаниям поля на некотором другом волновом фронте.