Единственность решения на примере уравнения типа свертки
Для интегрального уравнения Фредгольма
1-го рода с разностным ядром
справедливо следующее соотношение
где
-
спектр исходных данных,
- спектр решения, а
-
частотная характеристика линейной
системы.
Пусть частотная характеристика линейной
системы в интервале частот
тождественно равна 0. Сконструируем
функцию
таким
образом, что бы её спектр
был
отличен от 0 только на интервале
Пусть на вход рассматриваемой нами линейной системы поступает сумма сигналов и . В этом случае спектр сигнала на выходе системы будет определяться следующим соотношением
В силу условий наложенных нами на функции и второе слагаемое в этом выражении тождественно равно 0. Откуда следует что
Поскольку сигнал выбирался произвольным образом, за исключение ограничений наложенных на его спектр, то можно утверждать следующее:
Существует бесконечное множество входных воздействий, которые будучи поданы на вход линейной системы приведут к появлении на её выходе одного и того же отклика.
Таким образом, решение обратной задачи не является единственным, так как к полученному решению мы можем прибавить произвольную функцию, спектр которой удовлетворяет приведенным выше условиям. Выбрать одно решения из полученного бесконечного множества решений можно только при наличии дополнительной априорной информации.
Устойчивость решения
Рассмотрим последнее условие,
определяющее корректность обратной
задачи. Это условие устойчивости решения.
Вопрос об устойчивости решения возникает
в связи с тем, что правая часть уравнения
Фредгольма (функция
),
которая представляет собой исходные
данные для получения решения, никогда
не известна точно. Ошибка в определении
исходных данных вызвана целым рядом
причин. Основными из них являются шумы,
возникающие при формировании функции
и
ограниченная точность измерения этой
функции.
В наиболее простом случае правую часть
уравнения Фредгольма можно представить
в виде суммы двух функций: функции
,
представляющей точное значение отклика
системы и функции
,
описывающей шум, т.е. используя операторное
представление можно записать
В случае, когда шум отсутствует, то есть
,
решение этого уравнения находится с
помощью обратного оператора
такого,
что
Применение обратного оператора к
зашумленным исходным данным естественно
приведёт к появлению шума в решении.
Причем поскольку оператор L-1[]
– линейный, а функция
является аддитивной смесью точного
отклика
и
шума
,
то и решение будет суммой точного решения
и
шума
,
т.е.
Естественно возникает вопрос об отношении сигнал/шум в полученном решении и зависимости этого отношения от отношения сигнал/шум в исходных данных. Связь между соотношением сигнал/шум в исходных данных и соотношением сигнал/шум в решении определяет устойчивость решения обратной задачи. Если ограниченным значениям отношения сигнал/шум в исходных данных соответствуют ограниченные значения отношения сигнал/шум в решении, то решение является устойчивым. В противном случае решение неустойчиво.
Можно строго доказать, используя теорию интегральных уравнений, что в общем случае при решении уравнений Фредгольма сколь угодно малые значения уровня шума в исходных данных, т.е. значения функции n(x), могут привести к появлению неограниченно большого шума в решении, т.е. могут привести к неограниченному росту функции m(x). Таким образом в общем случае решение уравнения Фредгольма неустойчиво.
Неустойчивость решения обратных задач очень четко просматривается при решении интегральных уравнений типа свертки. Пусть
.
Используя теорему о свертке, запишем
.
Решение интегрального уравнения
.
Интеграл в правой части этого выражения представляет собой случайную ошибку решения. Энергия этой ошибки (дисперсия шума в решении задачи)
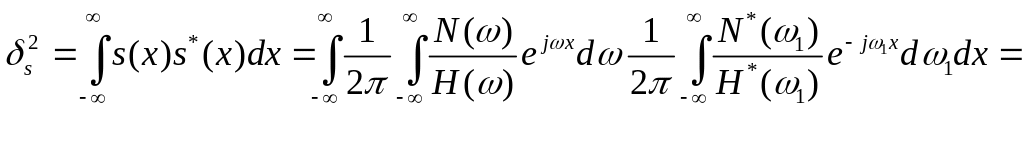
Для любых реальных приборов и систем
передаточная функция при
.
Поведение функции
согласовано с поведением функции
,
т.е. в точках, где
функция
также равна 0.
Функция
с
функцией
не согласована и поэтому, в точках или
областях, где
подынтегральное выражение стремится
к бесконечности, что приводит к расхождению
рассматриваемого нами интеграла, и как
следствие – к неустойчивости решения.