23. Метод неопределенных коэффициентов

Рассмотрим интегральное уравнение Фредгольма 1-го рода с симметричным ядром

где

Симметричность ядра интегрального уравнения гарантирует существование его собственных функций, их ортогональность и действительность собственных значений.

Будем считать, что множество собственных функций не только ортогонально, но и нормировано, т.е.

, где

Представим функции и в виде рядов по функциям :

, где

и

,

Подставив выражения для и в интегральное уравнение, получим:

и

Так как

То

Так как функции ортогональные, то . Отсюда следует, что а

В силу теоремы Пикара, для сходимости этого ряда необходимо, чтобы

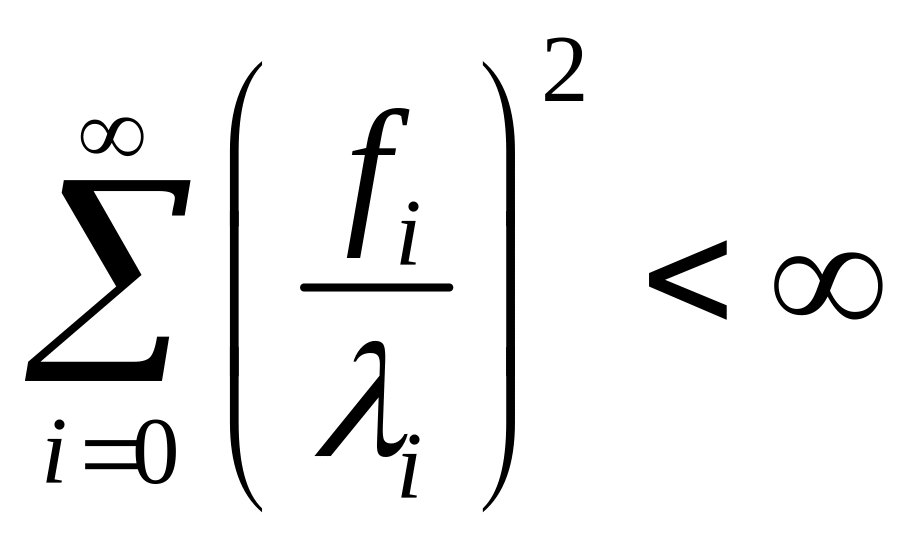
В общем случае функция При этом

Первая сумма этого соотношения является точным решением интегрального уравнения. Вторая сумма – представляет собой шум в решении, обусловленной ошибкой исходных данных. Оценим уровень этого шума, для чего определим дисперсию решения

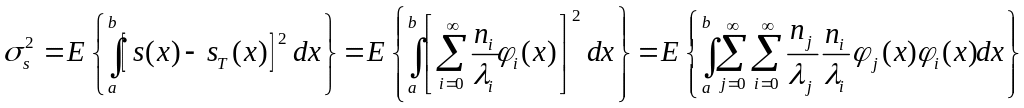
Так как множество функций ортонормированно то

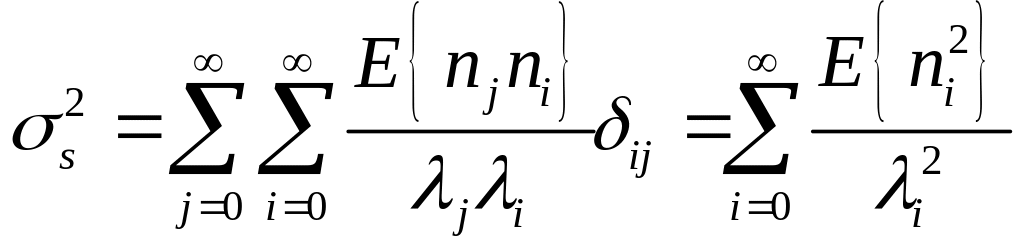
Оценим величину E [n_i²]. Для этого подставим n_i в явном виде:

Или

Используя соотношение

получим

Подставив (2.17) в (2.14) получим

Известно, что собственные значения _i убывают с увеличением i и при i     . В силу этого сумма в выражении для _S² неограниченно вырастает, т.е. мы получаем неустойчивое решение. Встает вопрос о его регуляризации.

При использовании данного метода восстановления изображения регуляризация оказывается достаточно "простой" и сводится к ограничению числа членов ряда для некоторой величиной N. В этом случае решение

При этом возникает ошибка, обусловленная неточность восстановления. Эта ошибка

Однако при этом ограничивается ошибка, вызванная неточностью или шумом исходных данных.

Недостатком этого алгоритма является то, что в большинстве случаев определение собственных функций интегрального уравнения само по себе представляет достаточно сложную задачу.

Пример решения обратной задачи

24. Коррекция искажений, вызванных равномерным прямолинейным движением объекта

При фотосъемке объектов, которые быстро движутся, будет получено смазанное изображение. Объясняется это тем, что за время экспозиции, то есть за время в течении которого объектив фотоаппарата открыт, объект смещается и на одном участке фотопленки фиксируется изображение разных участков объекта.

Разработаем математическую модель этого процесса. Введем несколько определений

• изображение объекта, сфокусированное на фотопленку, описывается функцией s(x, y).

• cмазанное изображение описывается функцией f(x,y).

• объект движется равномерно вдоль ось ОХ со скоростью V.

• время экспозиции равно .

Фотопленка является позитивной, линейной, не вносит шума и расположена на интервале

Поскольку движение происходит только вдоль одной оси координат, будем рассматривать одномерную задачу. Рассмотрим некоторую точку "смазанного" изображения и определим, каким образом значение функции в этой точке связано с функцией .

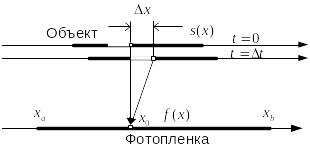
За время экспозиции объект сместится на расстояние . В точке суммируются значения точек функции , которые принадлежат интервалу . Точки расположенные вне этого интервала никакого вклада в формирование значения вносить не будут. В этом случае можно записать следующее соотношение

где

.

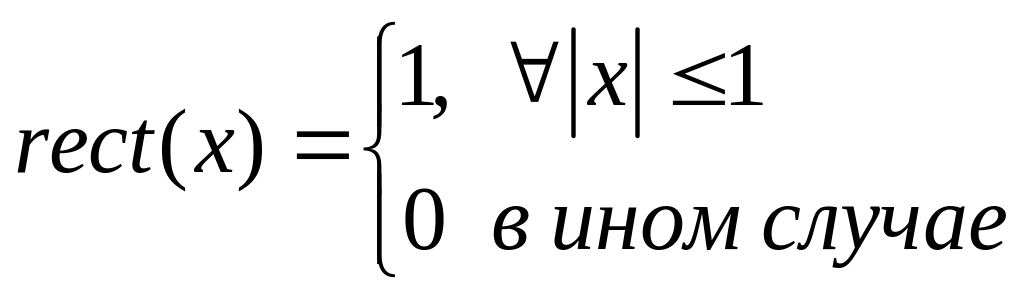Уравнение (26.1) представляет собой уравнение Фредгольма 1-го рода с разностным ядром, т.е. уравнение типа свертки. Ядром этого уравнения является функция .

В спектральной области это уравнение принимает следующий вид

,

где

.

Вычислим :

,

или

.

Подставив полученное соотношение в выражение , получим для спектра неискаженного изображения следующее соотношение

.

Вычислив обратное преобразование Фурье, получим:

.

Запишем полученное выражение в следующем виде, опустив -1 перед интегралом.

.

где функция .

Эта функция имеет бесконечное множество точек, в которых она обращается в нуль. Координаты этих точек определяются соотношением При наличии малейшего шума в исходных данных в области каждой из этих точек интеграл будет расходится – решение будет неустойчивым.

Для регуляризации решения используем стабилизирующий коэффициент

.

Подставим в соотношение выражение для частотной характеристики и выполним необходимые преобразования. В результате получим:

.

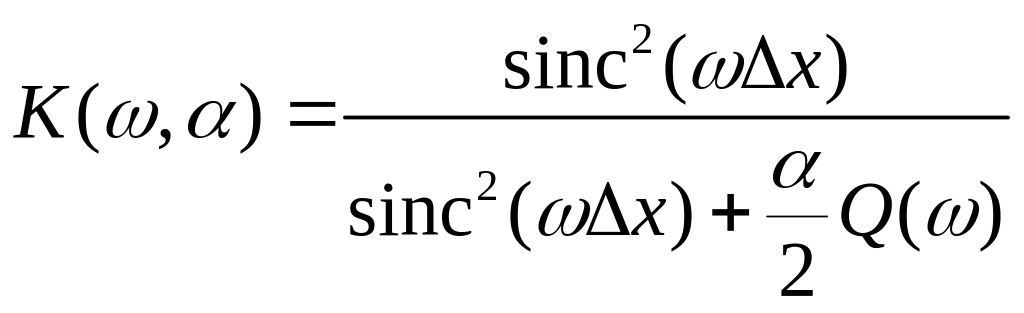Используя полученный стабилизирующий коэффициент, приближенное решение задачи запишется как

.

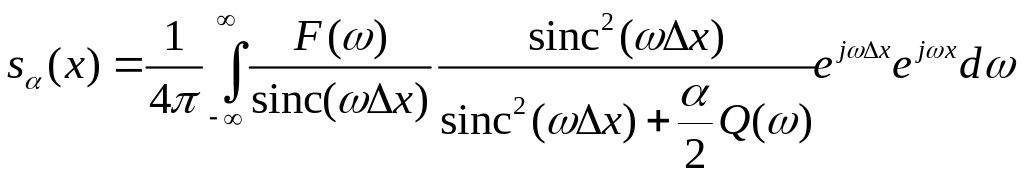Или

.

Для того, чтобы последнее выражение можно было использовать для восстановления смазанных изображений, необходимо задать функцию . В наиболее простом случае можно принять .