51. Алгоритм обратного проецирования

Рассмотрим еще одно соотношение, позволяющее вычислять обратное преобразование Радона. Пусть на плоскости XOY задана функция f(x,y), преобразованием Радона которой является функция R(s,). Функция R(s,) представляет собой интеграл от функции f(x,y) вдоль прямой, заданной уравнением

.

Зададим на плоскости XOY точку (x,y). В общем случае прямых, проходящих через эту точку и удовлетворяющих соотношению бесконечно много. Для любого угла  всегда можно определить значение s, при котором точка (x,y) будет принадлежать заданной прямой. Из всего множества значений функции R(s,) выберем те которые получены при интегрировании вдоль прямых проходящих через точку (x,y) и просуммируем эти значения. В результате получим функцию

,

которая называется суммарной обратной проекцией.

Выразим R(s,) через обратное преобразование Фурье:

Подставим последнее соотношение в выражение . В результате получим

.

В соответствии с теоремой о центральном сечении . После подстановки этого соотношения в выражение получим:

.

Поменяем пределы интегрирования в последнем выражении:

.

Объединяем пределы интегрирования:

.

С другой стороны, по определению спектра обратной проекции

.

Перейдем в последнем выражении к полярным координатам

.

.

Сравним подынтегральные выражения в и . Видно, что

,

или

.

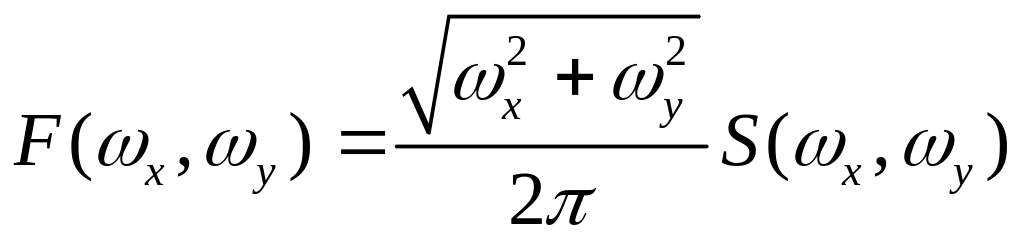Вычислив обратное преобразование Фурье, получим

.

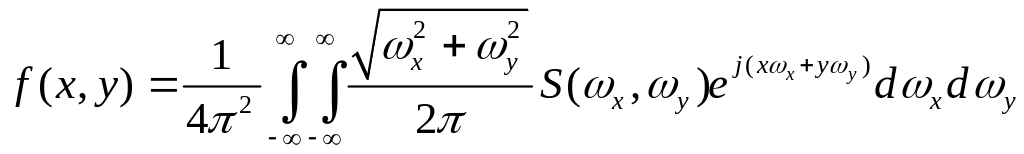Получено еще одно соотношение для вычисления преобразования Радона. Несмотря на то, что при выводе выражения и выражения использовались различные предпосылки, эти выражения полностью эквивалентны.

52. Вычисление обратного преобразования Радона

Мы получили два соотношения, позволяющие вычислять обратное преобразование Радона. Первое соотношение

получено на основе теоремы о центральном сечении. Второе

получено на основе понятия "обратная суммарная проекция".

Рассмотрим некоторые аспекты численной реализации этих алгоритмов. В соответствии с первым соотношением алгоритм вычисления обратного преобразования Радона заключается в следующем:

а). Вычисляется преобразование Фурье по переменной s от исходных данных R(s,);

б). Полученный спектр умножается на ;

в). Задается точка, координаты x и y которой подставляются в исходное соотношение либо и производится численное интегрирование.

Пункт в) повторяется для каждой точки, в которой определяются значения функции f(x,y). Такой способ вычисления требует значительных затрат машинного времени. Представим выражение в несколько ином виде

,

где .

Внутренний интеграл в этом выражении с точностью до коэффициента 1/2 представляет собой обратное преобразование Фурье функции . Обозначим его как

.

Так как для вычисления функции I(s можно использовать алгоритмы БПФ, то время вычисления обратного преобразования Радона можно значительно сократить, так как в этом случае функция

требует для вычисления только одномерное численное интегрирование.

Запишем выражение в дискретном виде:

,

где x_i и y_i - координаты точек в которых определяется значение функции f(x,y).

Для вычисления функции I(s используется некоторый численный алгоритм, например БПФ. Значения функции I(s рассчитываются в ряде фиксированных точек s_i, которые чаще всего расположены эквидистантно. Эквидистантным, обычно является и массив точек и . При эквидистантном расположении точек их координаты определяются следующими выражениями:

,

где - приращения соответствующих переменных.

При этом возникает следующая проблема. Для вычисления функции f(x,y) в соответствии с выражением необходимо иметь значения функции в точках

,

которые при изменении i, j, k не будут расположены эквидистантно.

Т.е. для вычисления функции нам необходимы значения функции в одних точках, а в действительности мы имеем значения функции для других точек.

Для определения значений функции в требуемых точках s_n используют те или иные методы интерполяции. В самом простом случае в качестве значения функции можно воспользоваться значение функции в ближайшей к s_n точке или определить значение функции в требуемой точке при помощи линейной интерполяции.

Необходимость в интерполяции приводит к увеличению объема вычислений с одной стороны, и к увеличению ошибок восстановления с другой.

Большой объем вычислений требуется и при использовании для восстановления изображений соотношения . Само соотношение вычисляется достаточно быстро. Однако больших вычислительных затрат требует расчет обратной проекции, спектр которой входит в это выражение.