48. Преобразование Радона точечного объекта

В качестве примера вычислим преобразование Радона от функции

.

Эта функция описывает точечный объект, расположенный на плоскости XOY в точке (x₀,y₀):

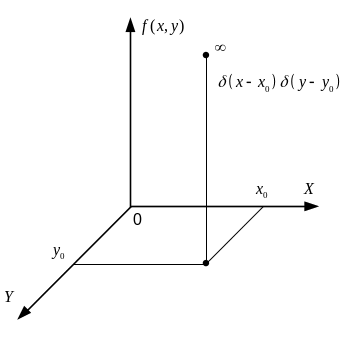
Подставим f(x,y) в выражение для преобразования Радона , сделав соответствующую замену переменных. В результате получим

.

Воспользуемся свойством  - функции , и преобразуем выражение , вынеся множитель :

Воспользуемся фильтрующим свойством -функции

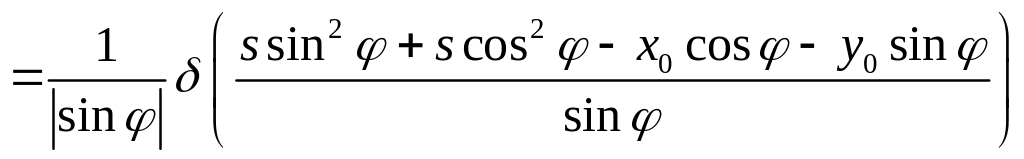
Внося множитель под знак дельта-функции, а также используя свойство симметричности,

.

Как следует из выражения , преобразование Радона точечного объекта представляет собой дельта-функцию, аргумент которой

,

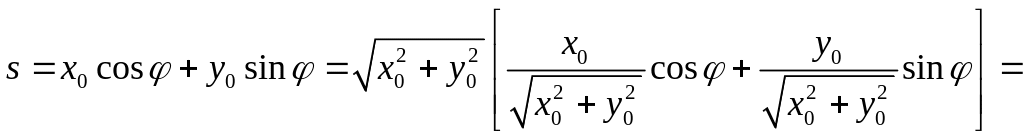
где

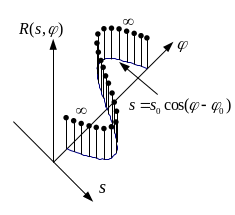
На следующем рисунке показано преобразование Радона для некоторых конкретных значений и .

49. Теорема о центральном сечении

Пусть задана функция двух переменных f(x, y) и для нее определены:

- двумерное преобразование Фурье F(_x, _y),

- преобразование Радона R(s,),

- преобразование Фурье R( от радоновского образа R(s,).

Покажем, что

.

Представим функцию в следующем виде:

.

Поменяем порядок интегрирования. В результате получим

.

После интегрирования переменной s (используем фильтрующее свойство дельта-функции):

.

Обозначим

 .

В этом случае

.

И нтеграл в правой части этого выражения ни что иное, как двумерное преобразование Фурье функции f(x y). Таким образом

.

Мы получили соотношение, которое связывает между собой преобразование Фурье радоновского образа функции с ее двумерным Фурье спектром. Это соотношение и называется теоремой о центральном сечении. Функция представляет собой поверхность в пространстве (_x, _y). Функция представляет собой сечение этой поверхности плоскостью проходящей через начало системы координат, перпендикулярной плоскости X0Y и направленной под углом  к оси _x.

50. Обратное преобразование Радона

Рассмотрим алгоритм обратного преобразования Радона, основанный на теореме о центральном сечении. Запишем функцию f(x, y) через обратное преобразование Фурье.

.

Перейдем от координат _x и _y к полярным координатам  и , где

.

При таком преобразовании координат коэффициенты Ламе равны 1 и , т.е. .

Пределы интегрирования определим от 0 до 2 для  и от 0 до  для . В результате получим

.

Так как по теореме о центральном сечении , то

.

Обычно преобразование Радона определено для углов 0    . Это связано с техническими особенностями получения экспериментальных данных. Преобразуем полученное нами соотношение таким образом, чтобы угол  находился в указанных выше пределах. Для этого интервал интегрирования по  разобьем на два интервала и заменим во втором из них величину  на +. В результате получим

Сделаем во втором интеграле подстановку и поменяем местами пределы интегрирования:

.

Ранее было показано, что . Аналогичное соотношение можно получить и для Фурье спектра преобразования Радона:

.

Воспользуемся соотношением и сделаем соответствующую подстановку в . При этом

.

Объединив интервалы интегрирования, получим

.

Полученное выражение является обратным преобразованием Радона, используя которое можно восстановить функцию по ее радоновскому образу . Как видно из этого выражения, математически связь неизвестной величины и известной описывается преобразованием, похожим на преобразование Фурье. Таким образом, несмотря на качественные физические различия рассмотренных ранее обратных задач и данной обратной задачи, математический аппарат их решения оказывается похожим.