54. Итерационные алгоритмы с ограничениями

Предварительные сведения о поведении решения обратной задачи можно выразить посредством некоторого оператора такого, что . В этом случае оператор может использоваться в итерационном методе для уточнения решения на каждом шаге итерации.

Если решение неотрицательно, то оператор можно задать с помощью оператора положительности, для которого введено специальное обозначение :

Если известно, что спектр решения ограничен частотой ₀, то соответствующим оператором ограничения в частотной области будет оператор.

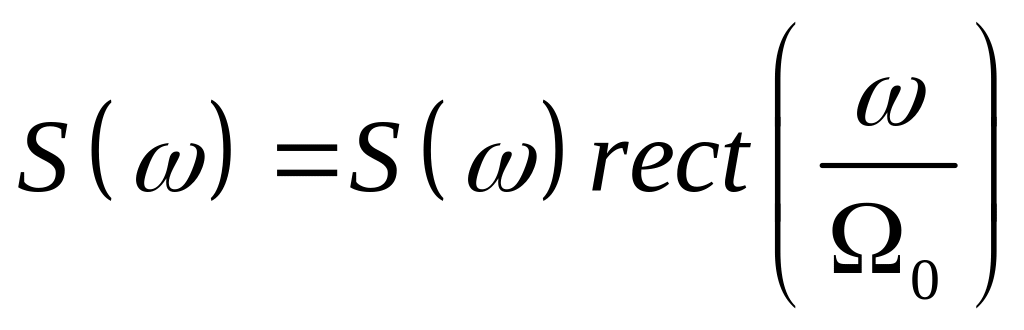
Переходя от спектра к самой функции и учитывая то, что обратное преобразование Фурье от функции rect( ) есть функция вида sin x/x, а произведение спектров соответствует свертке функции, получим выражение для оператора ограничения частоты B [ ]:

.

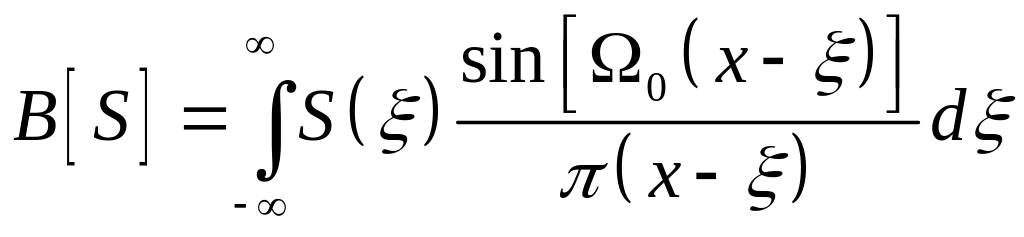55. Итерационное уравнение

Пусть прямая задача задается следующим операторным уравнением:

Запишем следующее тождество

,

где  - некоторая константа, LC[ ] – обозначает последовательное применение операторов C и L.

Преобразуем это тождество:

.

Введем оператор

.

В результате можем записать некоторое итерационное уравнение

,

Для того, чтобы оператор можно было использовать в качестве итерационного оператора, необходимо чтобы он был оператором сжатия, т.е.

, где

В классе L₂ расстояние между функциями определяется как

.

Тогда

Обозначим

,

Тогда

Таким образом, оператор будет оператором сжатия в том случае, если оператором сжатия будет оператор .

Оператор G[] будет являться линейным при условии линейности оператора C[]. В этом случае

Оператор будет оператором сжатия в том случае, если выполняется неравенство :

Условие выполнения этого неравенства для каждого конкретного случая определяется видом операторов и , входящих в оператор .

56. Ряд Неймана

Одним из достоинств итерационных алгоритмов является то, что при их использовании нет необходимости определять оператор, обратный оператору прямой задачи. Это свойство итерационных алгоритмов является весьма существенным, так как определение обратного оператора для уравнений с неразностным ядром представляет достаточно сложную и не всегда разрешимую задачу.

Однако, представив решение задачи в виде итерационного процесса, достаточно просто представить обратный оператор в виде разложения в ряд оператора прямой задачи. Такой ряд называется рядом Неймана.

Мы говорили, что при использовании итерационного оператора последовательность приближенных решений можно представить в следующем виде:

где оператор

Допустим, что при оператор является оператором сжатия. Запишем последовательность приближенных решений для случая, когда начальное приближение S₀ = f. Получим следующий ряд:

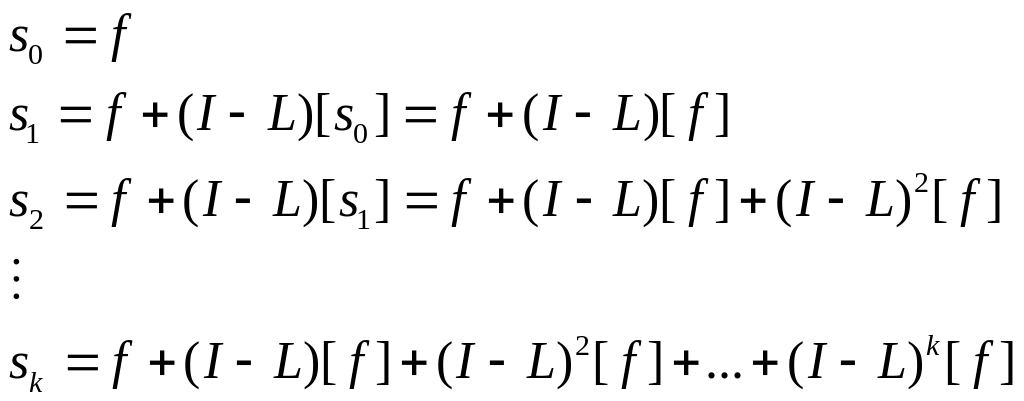
Или

,

где означает последовательное применение k раз оператора к функции f, а .

Так как при , т.е. последовательность приближенных решений стремиться к точному решению), то

,

Так как

,

есть решение обратной задачи, то на основании выражений и запишем для обратного оператора следующее соотношение

,

Ряд в правой части данного равенства называется рядом Неймана.

Данное соотношение получено при одном единственном условии, которое заключается в том, что оператор должен быть оператором сжатия. Поэтому разложение обратного оператора в ряд Неймана применимо к любому интегральному уравнению Фредгольма 1-го рода независимо от типа его ядра.