21. Управляемая линейная фильтрация. Фильтр Бэйкуса-Гильберта

В основу фильтра Тихонова и фильтра Винера положен принцип минимизации уровня шума в получаемом изображении. При этом изображение оказывается сильно сглаженным, т.е. при использовании этого типа фильтрации в изображении исчезают мелкие детали, контуры более крупных деталей оказываются размытыми. В то же самое время субъективные оценки качества таких изображений, т.е. оценки даваемые человеком-экспертом, склоняются в сторону более зашумленных, но менее сглаженных изображений, т.е. человек воспринимает, как более качественное, четкое изображение с большим уровнем шумов, чем нечеткое, но с малым уровнем шумов.

В этой связи с этим был разработан фильтр, в котором можно задавать соотношение между степенью сглаживания и уровнем шума.

Пусть дисперсия шума в восстановленном изображении , а дисперсия ошибки восстановления, т.е. ошибки, вызванной использованием приближенного оператора , Определим некоторую величину:

и подберем оператор восстановления так, чтобы величина M была минимальной. В этом случае постоянные _m и _s будут определять соотношение между уровнем случайного шума в изображении и степенью сглаженности изображения. Запишем M в явном виде:

,

где

.

Будем считать, что шум n(x) и изображение стационарные, статистически независимые процессы со спектральными плотностями R_N() и R_S().

Тогда воспользовавшись выкладками, приведенными в предыдущем параграфе, получим

Включим коэффициенты 1/2 в постоянные _m и _s и подставим выражение для частотной характеристики приближённого обратного оператора в выражение для M. В результате получим

,

где K() – стабилизирующий коэффициент.

Теперь нам осталось определить K() так, что бы величина M была минимальной. Так как подынтегральное выражение не отрицательно, то минимум будет в точке, в которой первая производная подынтегрального выражения по K() будет равна нулю, а вторая будет положительна:

.

Вычислив производную, получим

После несложных преобразований найдём

Нетрудно убедится в том, что вторая производная от полученного значения всегда больше нуля.

Так определяется стабилизирующий коэффициент, для которого М принимает минимальное значение.

Этому стабилизирующему коэффициенту соответствует фильтр с передаточной функцией

Фильтр с такой частотной характеристикой называется фильтром Бэйкуса-Гильберта.

22. Гомоморфная фильтрация

Фильтр Бейкуса-Гильберта, как и фильтр Тихонова и параметрический фильтр Винера, имеет только один параметр для управления передаточной фильтрацией. Этот параметр

При практической обработке изображений варьирование этим параметром во многих случаях не дает положительных результатов, так как его незначительные изменения могут привести к сильной зашумленности изображения. Это привело к появлению других способов управления частотной характеристикой восстанавливающего фильтра и одним из таких методов является метод гомоморфной фильтрации.

Основная идея гомоморфной фильтрации заключается в определении такого восстанавливающего фильтра, который позволили бы получить заданную спектральную плотность восстановленного изображения.

Для каждого изображения объекта S(x) можно рассчитать спектральную плотность мощности R_S(). Так как S(x) – случайная функция, то R_S() также является случайной функцией. Однако в ряде случаев можно ограничить класс объектов таким образом, что функции R_S() отдельных объектов из этого класса будут близки друг к другу. В этом случае можно ввести усредненную для этого класса объектов спектральную плотность мощности.

Под гомоморфным фильтром понимают фильтр с передаточной функцией, для которой выполняется следующее соотношение:

в предложении, что изображение и шум статистически независимые, стационарные случайные процессы.

Для определения передаточной функции Y() раскроем это выражение:

Так как S() и N() статистически независимые случайные процессы то

.

Кроме этого

,

.

Используя эти соотношения, получим

.

или

.

Решим это уравнение относительно Y(). В результате имеем

.

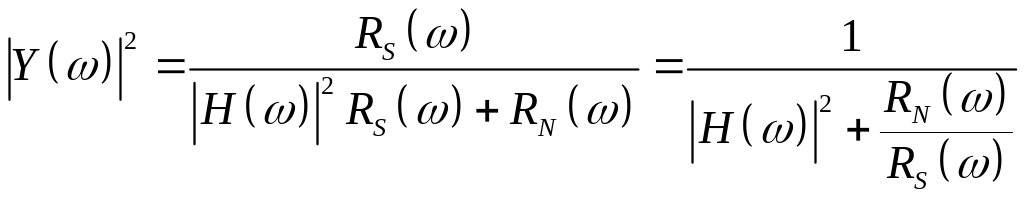Фильтр с такой характеристикой представляет собой среднегеометрическое между фильтром Винера и инверсным фильтром в случае если H() – действительная функция

Как дальнейшее развитие гомоморфного среднегеометрического фильтра был предложен так называемый управляемый эволюционный фильтр с передаточной функцией следующего вида

Этот фильтр охватывает все случаи фильтрации, рассмотренные нами. Так при  = 1,  = 0 мы получаем инверсный фильтр, при  = 0,  = 1 – фильтр Винера или фильтр Тихонова (в зависимости от вида функции ), при  = ½,  = ½ - гомоморфный, среднеквадратичный фильтр.