20. Оптимальный фильтр Винера

При построении фильтра Тихонова мы исходили из того, что нам известна дисперсия шума в исходных данных, т.е. величина ² . Зная эту величину по невязке мы определили оптимальное значение регуляризирующего коэффициента  для заданной функции Q().

Рассмотрим случай, когда у нас имеется более обширная информация о шуме и поведении решения.

В общем случае исходные данные мы представляли в виде суммы точного значения исходных данных и шума, т.е. в виде

.

Так как шум n(x) это случайный процесс, то и исходные данные являются f(x) также являются случайным процессом. Кроме этого решение s(x) также будет случайной функцией. В противном случае его не надо было бы искать.

Если параметры этих случайных процессов известны, то их (параметры) можно использовать в качестве априорной информации при разработке алгоритма восстановления.

Пусть функции s(x) и n(x)являются реализациями стационарных, некоррелированных между собой случайных процессов, и известны спектральные плотности мощности этих процессов R_S () и R_N().

Тогда задачу определения оптимального регуляризирующего оператора сформулируем следующим образом: найти оператор, который минимизирует величину среднеквадратичного отклонения получаемого решения от точного, т.е. минимизирует величину E[S_(x)–S_T(x)]² , при известных функциях R_S() и R_N(), где E [ ] – знак математического ожидания.

Пусть такому оператору соответствует стабилизирующий множитель K( ). Составим уравнение для его определения.

Для определения математического ожидания квадрата разности функций используем следующие соотношения:

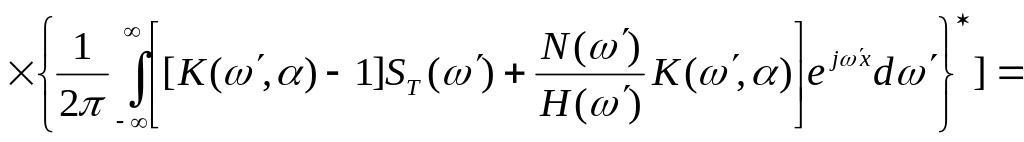
Так как S_T() и N() – некоррелированные случайные процессы по условию, то

Кроме того

Подставив в подынтегральные выражения значения математических ожиданий, получим

.

Или

Нам необходимо минимизировать значение полученного интеграла путем выбора соответствующего стабилизирующего множителя K(,.). Для этого найдем первую производную от подынтегрального выражения по K(, ) и приравняем ее к нулю.

Так как вторая производная по K(,) равна R_S() + R_N()/|H()|²  0, то условие является условием минимумом. Отсюда следует

Или

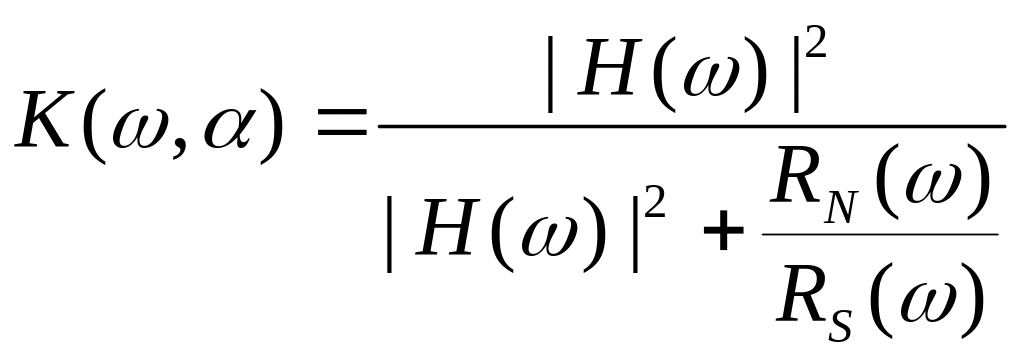
Обратный оператор, соответствующий данному стабилизирующему коэффициенту имеет следующий вид:

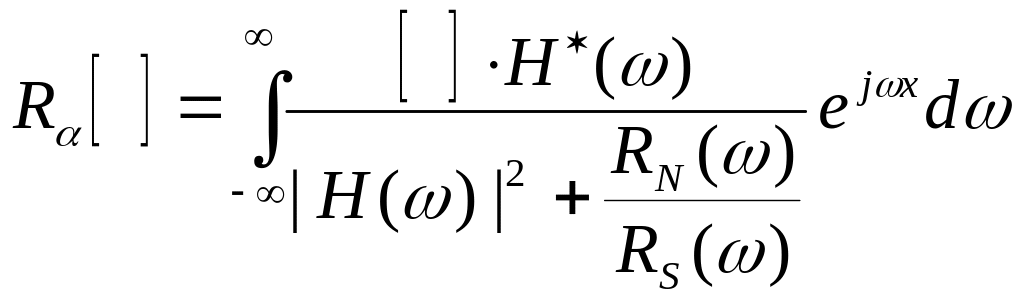
Применение тихоновской или винеровской фильтрации к обработке изображений далеко не всегда дает положительные результаты. Объясняется это тем, что математические критерии, положенные в основу этих фильтров, не соответствуют критериям качества изображений. Восприятие зрительных образов человеком сложный и неизученный, на сегодняшний день, физиологический процесс. Отсутствие достаточно точных моделей обработки зрительной информации головным мозгом человека, приводит к невозможности получения математических критериев качества изображений воспринимаемых человеком. Это в значительной степени усложняет процесс обработки и приводит к тому, что в процессе обработки изображений с целью улучшения качества их субъективного восприятия должен принимать участие эксперт или группа экспертов. При этом предполагается, что в процессе обработки есть возможность изменять те или иные параметры обратного оператора с помощью которого восстанавливается изображение.

В случае тихоновской фильтрации таким параметром является параметр регуляризации . В случае оптимального фильтра Винера такой параметр отсутствует. Для придания большей гибкости винеровской фильтрации был предложен видоизмененный стабилизирующий коэффициент

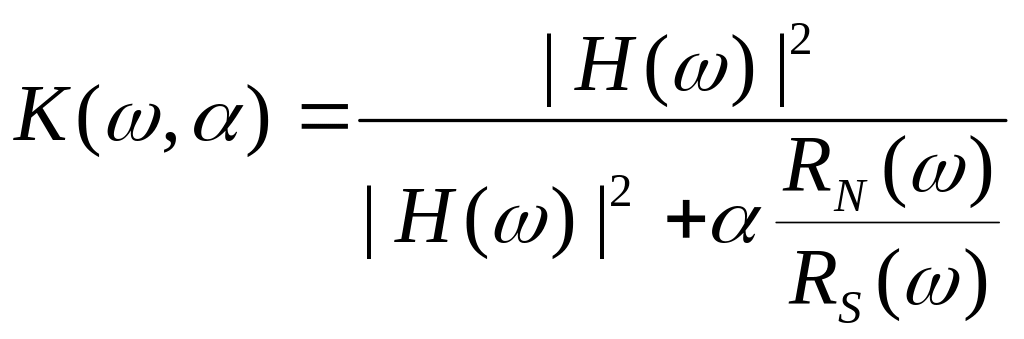
Этому стабилизирующему коэффициенту соответствует обратный оператор

Такой фильтр называется параметрическим фильтром Винера.