3. Уравнение первого порядка с разделяющимися переменными

Дифференциальное уравнение первого порядка вида

f₁(y)dy = f₂(x)dx (1)

с непрерывными функциями f₁(у) и f₂(x) принято называть уравнением с разделенными переменными.

Если функция у=у(х) является решением этого уравнения, то при подстановке этой функции у(х) в уравнение (1) мы получим тождество, интегрирование которого дает

, (2)

где С – произвольная постоянная.

Уравнению (2) удовлетворяют все решения уравнения (1), причем каждое решение уравнения (2) является решением уравнения (1), ибо если функция у(х) обращает в тождество уравнение (2), то, дифференцируя это тождество, мы получим, что y(x) удовлетворяет и уравнению (1).

Под неопределенными интегралами, стоящими в равенстве (2), можно понимать любые первообразные функций f₁ и f₂, причем эти первообразные можно брать в форме интегралов с переменным верхним пределом, т. е. равенство (2) можно переписать в виде

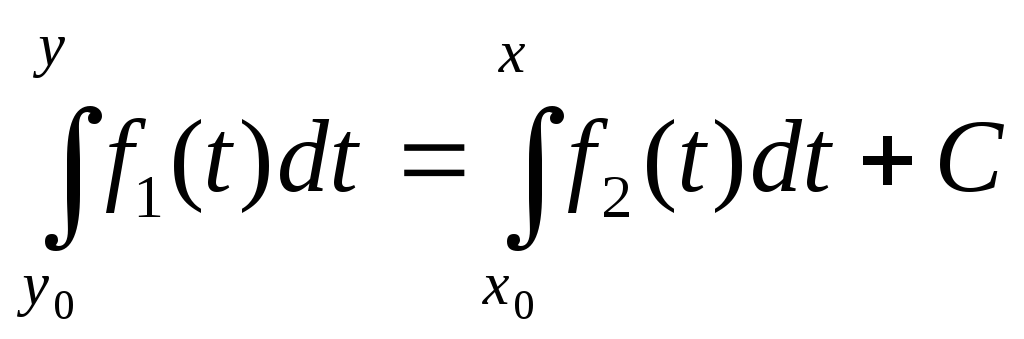, (3)

где х₀ и у₀ — любые две точки, в окрестностях которых определены и непрерывны функции f₂(x) и f₁(y).

Для получения решения дифференциального уравнения (1), удовлетворяющего произвольному начальному условию у(х₀)=у₀, следует положить в (3) x= х₀, у = у₀. При этом получим, что С = 0, и потому решение уравнения (1), удовлетворяющее начальному условию у(х₀) = у₀, определяется равенством

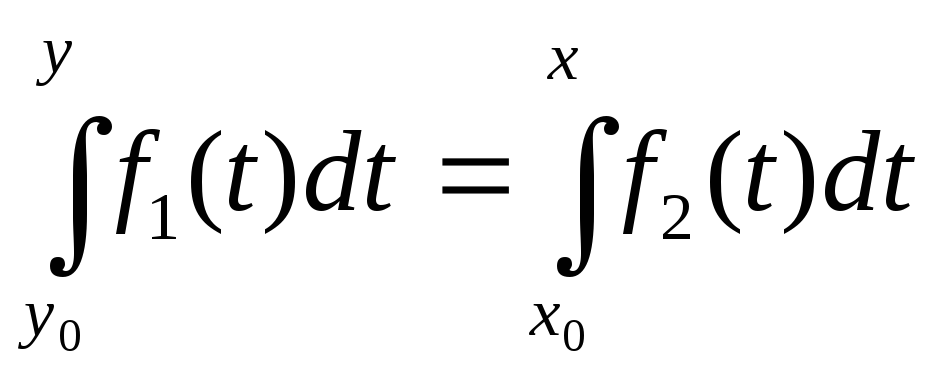. (4)

Дифференциальное уравнение вида

, (5)

в котором коэффициенты при дифференциалах распадаются на произведение множителей, каждый из которых зависит только от х или только от у, называется дифференциальным уравнением с разделяющимися переменными, ибо путем деления на ψ₁(y)φ₂(x) это уравнение приводится к рассмотренному выше уравнению с разделенными переменными

. (6)

Единственное, о чем нужно заботиться, — это возникающая при делении на ψ₁(y)φ₂(x) возможная потеря частных решений, обращающих в нуль произведение ψ₁(y)φ₂(x).

Впрочем, легко проверить, что в случае, если число х = а является корнем уравнения φ₂(x)=0, дифференциальное уравнение (5) кроме решений, определяемых из уравнения (6), имеет дополнительное решение х = а, а в случае, если число у = b является корнем уравнения ψ₁(y)=0, дифференциальное уравнение (5) имеет дополнительное решение у = b.

В качестве примера рассмотрим уравнение

. (7)

Разделяя переменные, получим уравнение

, (8)

в котором функции (1+y²) и (1+x²) не обращаются в нуль. Поэтому все решения уравнения (7) получаются интегрированием уравнения (8) и имеет вид

Эти решения можно переписать в виде

ln(1+y²)=ln(1+x²)+lnC_1,

где С₁- произвольная положительная постоянная.

Окончательно получим, что 1+y²=C₁(1+x²).

4. Однородные дифференциальные уравнения первого порядка

Дифференциальные уравнения первого порядка, имеющие вид

(1)

принято называть однородными. Эти уравнения сводятся к уравнениям с разделяющимися переменными посредством замены искомой функции y(x) на новую искомую функцию .

Действительно, при такой замене y(x)=xu(x), y′=xu′+u, вследствие чего (1) переходит в уравнение xu′+u=f(u), которое можно переписать в виде

Интегрируя последнее уравнение, получим, что , где С₁ – произвольная положительная постоянная, так что окончательно

.

Рассмотрим уравнение

Полагая y(x)=xu(x) и учитывая, что y′=xu′+u, приведем уравнение к виду xu′+u=u+tgu, эквивалентному .

Интегрируя последнее равенство и обозначая С₁ произвольную положительную постоянную, получим ln|sinu|=ln|x|+lnС₁, откуда следует, что

sinu=C₁x,т.е. .