Понятие базиса. Аффинные координаты

Определение 1. Три линейно независимых вектора образуют в пространстве базис, если любой вектор может быть представлен в виде линейной комбинации векторов .

Аналогично определяется базис на плоскости .

Определение 2. Два лежащих в плоскости  линейно независимых вектора образуют на этой плоскости базис, если любой лежащий в этой плоскости вектор может быть представлен в виде линейной комбинации векторов .

Имеют место следующие фундаментальные утверждения:

1) любая тройка некомпланарных векторов образует базис в пространстве;

2) любая пара лежащих в данной плоскости неколлинеарных векторов образует базис на этой плоскости.

Теорема. Каждый вектор может быть единственным способом разложен по базису :

.

Числа    называются координатами вектора относительно базиса .

Теорема. При сложении двух векторов их координаты складываются. При умножении вектора на любое число  все его координаты умножаются на это число.

Аффинные координаты в пространстве определяются заданием базиса и некоторой точки О, называемой началом координат.

Аффинными координатами любой точки М называются координаты вектора (относительно базиса ).

Свойства базиса и понятие аффинных координат на плоскости аналогичны случаю пространства.

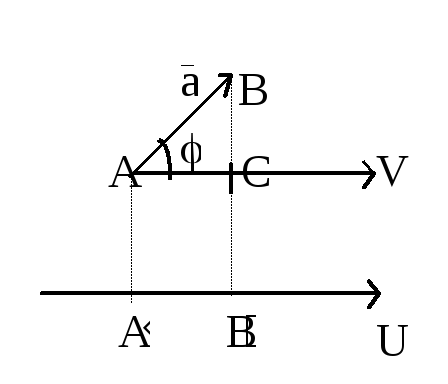
Проекция вектора на ось

Определение. Проекцией вектора на ось U называется величина направленного отрезка оси U, где - основания перпендикуляров, опущенных на ось U из точек A и B соответственно(рис.10).

Теорема Проекция вектора на ось U равна длине вектора , умноженной на косинус  угла наклона вектора к оси U.

Доказательство.

Обозначим через V ось, проходящую через начало A вектора и имеющую тоже направление, что и ось U, и пусть C- проекция B на ось V.

BAC=, = AC.

Так как по определению при, то при.

Но cos=cos. Следовательно при и т.д.

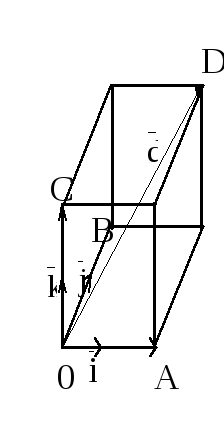
Декартова прямоугольная система координат (дпск) в пространстве.

ДПСК является частным случаем аффинной системы, отвечающим тройке взаимно ортогональных и единичных базисных векторов. Принято направления векторов брать совпадающими с направлением декартовых осей Ox, Oy, Oz соответственно.

Нами получено, что любой вектор может быть, причем единственным способом, разложен по декартову прямоугольному базису (ДПБ), т.е. для каждого вектора существует единственная тройка чисел X, Y, Z такая, что

. (1)

Числа X, Y, Z называются декартовыми прямоугольными координатами (ДПК) вектора . Если M- любая точка пространства, то ДПК этой точки совпадают с ДПК вектора .

Вектор будем также записывать в виде .

Теорема. ДПК вектора равны проекциям этого вектора на оси OX, OY и OZ соответственно.

Доказательство.

. , т.к. из и того, что , получаем . Но знаки OA и X совпадают,

так как. когда векторы направлены в одну сторону , оба числа OA и X положительны, а в случае, когда векторы направлены в противоположные стороны, оба числа OA и X отрицательны. Т.е. OA=X.

Аналогично OB=Y, OC=Z, ч.т.д.

Обозначим , ,  углы наклона вектора к осям Ox, Oy, Oz соответственно. Числа cos, cos, cos называют направляющими косинусами вектора .

Из теорем имеем

(2)

Т.к. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то из равенств OA=X, OB=Y, OC=Z получим выражение для длины вектора через его координаты:

(3)

Из формул (1) и (2) имеем:

, .

Возводя в квадрат и складывая последние равенства, получим