
- •Оглавление
- •Общие методические указания по изучению дисциплины
- •Основные теоретические положения математического анализа
- •Теория множеств
- •Основные свойства и графики элементарных функций
- •Предел функции, непрерывность функции, производная функции
- •Анализ функций одной и двух переменных
- •Интегрирование функций
- •Определенный интеграл, основные теоремы
- •Способы интегрирования
- •Дифференциальные уравнения
- •Понятие дифференциального уравнения
- •Дифференциальные уравнения первого порядка Общие сведения
- •Уравнение первого порядка с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Линейное уравнение первого порядка
- •Векторная алгебра
- •Понятие вектора и линейные операции над векторами Понятие вектора
- •Линейные операции над векторами
- •Свойства сложения векторов:
- •Понятие линейной зависимости векторов
- •Линейные комбинации двух векторов
- •Линейные комбинации трех векторов
- •Понятие базиса. Аффинные координаты
- •Проекция вектора на ось
- •Декартова прямоугольная система координат (дпск) в пространстве.
- •Полярная система координат
- •Скалярное произведение двух векторов Определение скалярного произведения (сп)
- •Геометрические свойства сп
- •Алгебраические свойства сп
- •Выражение скалярного произведения (сп) в декартовых прямоугольных координатах (дпк)
- •Векторное произведение двух векторов Правые и левые тройки векторов и системы координат
- •Векторное произведение двух векторов (вп)
- •Геометрические свойства вп
- •Алгебраические свойства векторного произведения (вп)
- •Понятие матрицы и определителя второго и третьего порядка
- •Выражение векторного произведения (вп) в декартовых прямоугольных координатах (дпк)
- •Смешанное произведение трех векторов
- •Выражение смешанного произведения в декартовых координатах
- •Аналитическая геометрия на плоскости
- •Различные виды уравнений прямой на плоскости Общее уравнение прямой
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой в отрезках
- •Каноническое уравнение прямой
- •Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
- •Кривые второго порядка
- •Эллипс Определение эллипса и вывод его канонического уравнения
- •Исследование формы эллипса
- •Эксцентриситет эллипса
- •Гипербола Определение гиперболы и вывод ее канонического уравнения
- •Исследование формы гиперболы
- •Асимптоты гиперболы
- •Равнобочная гипербола
- •Сопряженная гипербола
- •Эксцентриситет и фокальные радиусы гиперболы
- •Парабола Определение параболы и ее уравнение
- •Исследование формы параболы
- •Общее свойство кривых второго порядка - эллипса, гиперболы и параболы Директриса эллипса, гиперболы и параболы
- •Аналитическая геометрия в пространстве Плоскость как поверхность первого порядка
- •Неполные уравнения плоскости
- •Уравнение плоскости в отрезках
- •Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •Уравнение прямой в пространстве
- •Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой
- •Некоторые дополнительные предложения и примеры
- •Линейная алгебра
- •Матрицы. Основные определения
- •Действия над матрицами
- •Обратная матрица
- •Системы линейных уравнений Система линейных уравнений
- •Методы решения системы n линейных уравнений с n неизвестными
- •Методы решения системы m линейных уравнений с n неизвестными. Метод Гаусса
- •Система m линейных уравнений с n переменными
- •Задачи оптимизации
- •Математические модели оптимизации
- •Задачи линейного программирования
- •Задачи динамического программирования
- •Примеры решения типовых задач Задачи по математическому анализу, линейной алгебре и методам оптимизации
- •Варианты заданий к контрольным работам
- •Контрольная работа №1
- •Задача 6. Аналитическая геометрия на плоскости а) Линии первого порядка
- •Контрольная работа №2
- •Задачи для самостоятельной работы Пределы и непрерывность
- •Производная и ее применение
- •Определенный интеграл
- •Несобственные интегралы
- •1. Дифференциальные уравнения первого порядка
- •2. Однородные дифференциальные уравнения первого порядка
- •Вопросы к зачету
- •Определенный интеграл, основные теоремы.
- •Вопросы к экзамену
- •Определенный интеграл, основные теоремы.
- •Системы линейных уравнений.
- •Задачи линейного программирования.
- •Литература
- •К.Т.Н., доц. Тугуз Юрий Рамазанович Математика
- •Учебно-методическое пособие
- •344002, Г. Ростов-на-Дону, ул. Пушкинская, 70
-
Задачи динамического программирования
Динамическое программирование изучает методы оптимального управления многошаговым процессом, в котором решение, принимаемое на данном шаге, влияет на развитие процесса на последующих шагах.
Изучая многошаговый процесс, нужно в первую очередь выделить следующие его характеристики:
-
переменные, описывающие состояние процесса в начале (конце) каждого шага, так называемые фазовые координаты;
-
переменные, управляющие процессом, т.е. изменяющие его состояние, так называемое управление:
-
показатель, с помощью которого оценивается эффективность управления, так называемый критерий эффективности (целевая функция).
Идея динамического программирования состоит в том, что одновременная оптимизация критерия эффективности сразу по всем управлениям за m шагов заменяется последовательностью m одношаговых оптимизаций части переменных, относящихся только к одному шагу. Такой подход позволяет на каждом шаге с номером i найти условие ui(S) в предположении, что в начале этого шага система находится в любом из возможных состояний S.
Нахождение условного оптимального управления основано на принципе оптимальности, впервые сформулированном Р. Беллманом. Каковы бы ни были первоначальное состояние и предыдущие управления, последующие управления должны быть оптимальными относительно состояния, полученного в результате предыдущих управлений.
Принцип оптимальности Беллмана применяют последовательно ко всем шагам (обычно от последнего к первому), предполагая, что процесс каждого шага находится в любом из возможных состояний S. Это позволяет определить условно оптимальные управления ui(S) (i=1,2,3,..m) для каждого шага. Окончательные оптимальные управления можно найти, если рассмотреть процесс снова, от первого шага к последнему.
В применении к задаче распределения ресурсов алгоритм можно изложить следующим образом.
Пусть дано n функций (с неотрицательными значениями) f1(x), где xdi, f2(x), где xd2, …, fn(x), где xdn. Нужно определить max (min) функции
F(x1,x2,…,xn)=f1(x1)+f2(x2)+…+fn(xn),
причем на переменные x1, x2, …, xn наложена система ограничений, при которых, как мы будем предполагать, max(min)F существует.
В нашей задаче эта система сводится к уравнению x1, x2, …, xn =А. Чтобы найти
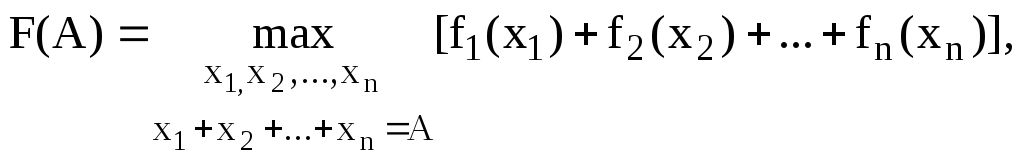
мы выполняем следующие этапы или шаги, используя рекуррентные соотношения:
![]()
![]()
…
![]()
![]()
Таким образом, вычисляется max[f1+f2] для всех x1 и x2 таких, что x1+x2=А. Так получают max[F1,2+f3] для различных x1, x2 и x3 таких, что x1+x2+x3=А, затем получают F1,2,3(А) и т.д.
В этой задаче и ее описании природа ограничений позволяет при последовательной оптимизации действовать в произвольном порядке, но далеко не всякая задача обладает этим свойством.
-
Примеры решения типовых задач Задачи по математическому анализу, линейной алгебре и методам оптимизации
Задача № 1
Описать свойства наиболее распространенных в экономике и управлении функций и построить их графики.
Задание
А
Параболическая функция
![]() .
.
Решение
Для
построения графика функции найдем
характерные точки. Вершина параболы
имеет координаты
![]()
![]()
При
![]() и
и
![]()
![]() .
Корни функции
.
Корни функции
![]()
|
|
Основные свойства этой функции.
1.Область
определения функции
2.Область
значений функции
3.Функция
убывает на интервале
4.Особые точки функции: корни (-1;0) и (3;0), минимум (-1;-4); пересечение с осью y (0;-3).
|
|
6. Функция симметрична относительно линии x=1. 7. Функция непериодическая.
8.
Функция имеет производные:
|
|
Задание
Б
.Экспоненциальная функция
![]() .
.
Решение
Для построения графика функции составим таблицу.
|
X |
-2 |
-1 |
0 |
1 |
2 |
|
Y |
-2.87 |
-2.64 |
-2 |
-0.3 |
4.2 |
|
|
Основные свойства этой функции.
1.Область
определения
2.Область
значений
3.Функция монотонно возрастает.
4.
Особые точки функции: (0;-2) и
5.Функция непрерывна. 6.Функция общего вида. 7.Функция непериодическая.
8.
Функция имеет производные
|
Задание
В.
Тригонометрическая функция
![]()
Решение
Для построения графика функции составим таблицу.
|
|
X |
|
0 |
|
|
|
|
|---|---|---|---|---|---|---|---|
|
|
Y |
-1 |
1 |
3 |
1 |
-1 |
|
|
|
Основные свойства функции.
1.Область
определения
2.Область
значений
3.Функция
возрастает в интервале
|
||||||
|
4.Особые
точки функции: (0;1), максимум
5.Функция непрерывна. 6.Функция нечетна относительно точки (0;1).
7.Функция
периодическая, период
8.
Функция имеет производные
|
|||||||
Задача №2
Найти
экстремумы и точки перегиба функции
одной переменной
![]() ,
построить график функции.
,
построить график функции.
Решение
Согласно выполнению необходимого условия существования экстремума найдем критические (стационарные) точки данной функции. Найдем первую производную функции и приравняем ее нулю:
![]() ,
, ![]() .
.
Решая
квадратное уравнение, получаем две
стационарные точки
![]() .
.
Согласно выполнению достаточного условия существования экстремума определяем характер поведения функции в стационарных точках.
Найдем вторую производную функции.
![]() .
.
Проверим
стационарную точку
![]() :
:
![]()
Так
как
![]() ,
то в этой точке функция имеет экстремум,
который является минимумом, потому что
,
то в этой точке функция имеет экстремум,
который является минимумом, потому что
![]() .
Вычислим значение этого минимума:
.
Вычислим значение этого минимума:
![]()
Проверим
стационарную точку
![]() :
:
![]() ,
,
Так
как
![]() ,
то в этой точке функция имеет экстремум,
который является максимумом, потому
что
,
то в этой точке функция имеет экстремум,
который является максимумом, потому
что
![]() .
Вычислим значение этого максимума:
.
Вычислим значение этого максимума:
.![]()
Для нахождения точек перегиба приравняем вторую производную нулю:
![]() ,
,
откуда
![]() .
.
|
|
График
функции
|
Задача №3
Найти
экстремумы функции двух переменных:![]() .
.
Решение
Согласно выполнению необходимого условия экстремума найдем критические (стационарные) точки данной функции.
Найдем частные производные первого порядка:
 ,
,
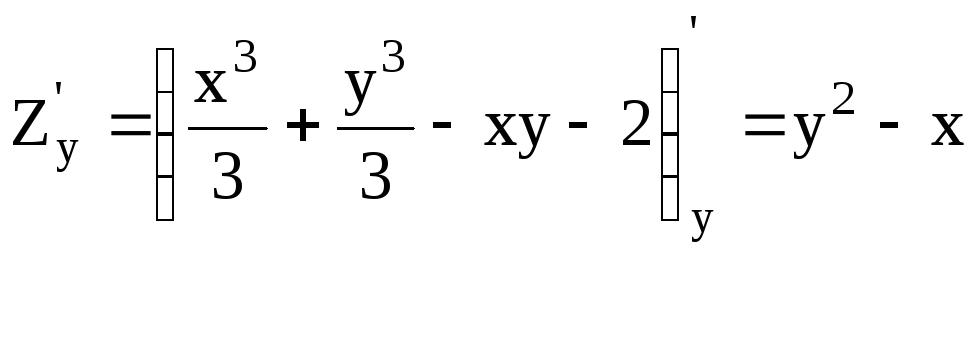 .
.
Приравняем полученные производные нулю:

Решая систему уравнений, отыщем стационарные точки.
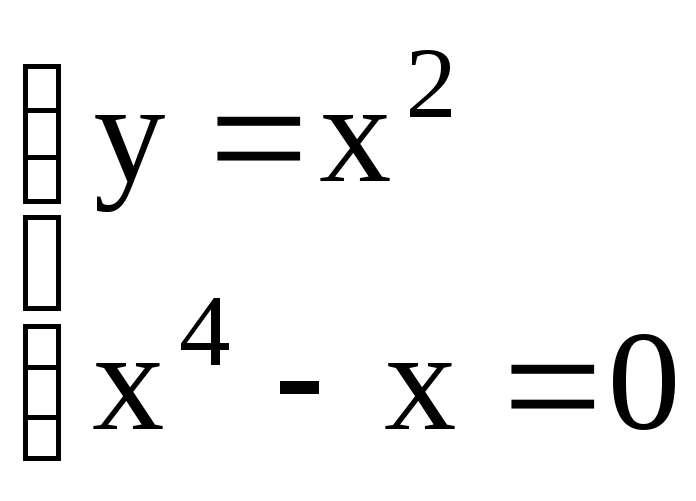
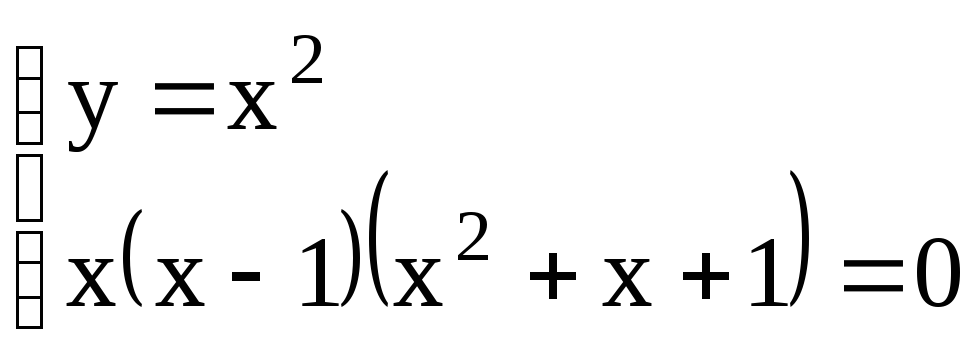
![]()
![]()
Таким
образом, находим две точки
![]() и
и
![]() .
.
Согласно выполнению достаточного условия существования экстремума определим характер поведения функции в стационарных точках.
Найдем все частные производные второго порядка.
 .
(А)
.
(А)
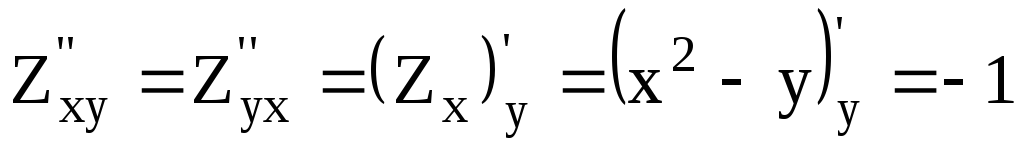 ,
(В)
,
(В)
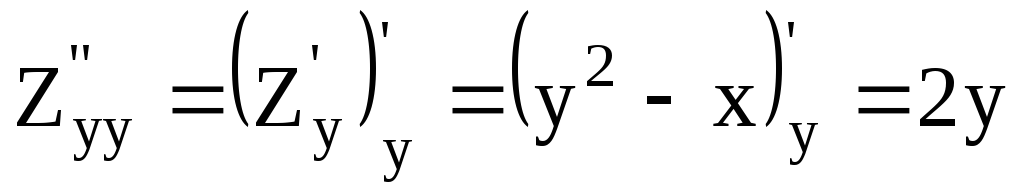 .
(С)
.
(С)
Проверим
стационарную точку
![]() :
:
![]()
![]()
![]()
![]() .
.
Так
как![]() ,
то в точке
,
то в точке![]() функция экстремума не имеет.
функция экстремума не имеет.
Проверим
стационарную точку
![]()
![]()
![]()
![]()
![]() .
.
Так
как
![]() ,
то в точке
,
то в точке![]() функция имеет экстремум, который является
минимумом, потому что
функция имеет экстремум, который является
минимумом, потому что
![]() и
и
![]() .
.
Вычислим значение этого минимума.
![]()
Задача №4
Задание
а). Проинтегрировать функцию
![]()
Решение
Применим
способ замены переменной, для подстановки
положим
![]() .
Дифференцируя, получим
.
Дифференцируя, получим
![]() и
и
![]() .
.
Поэтому
![]() .
.
Задание
б). Проинтегрировать рациональную
функцию
![]() .
.
Разложим подынтегральную функцию на простейшие дроби:
![]() .
.
Освобождаясь от знаменателя, получим:
![]()
Полагая
последовательно
![]() ,
получим
,
получим
![]() ,
откуда А=3; В=-1; С=-2.
,
откуда А=3; В=-1; С=-2.
Итак,
тождественно
![]() ,
поэтому
,
поэтому
![]()
Задание
в). Вычислить определённый интеграл
![]() .
.
Применим
способ интегрирования по частям.
Обозначим
![]() .
Тогда
.
Тогда
![]() и
и
![]() Применяя формулу интегрирования по
частям, получим
Применяя формулу интегрирования по
частям, получим
![]()
Задача 5
Дано уравнение гиперболы 16х2-9у2=144. Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнения директрис и асимптот гиперболы.
Решение.
Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса:
![]() или
или
![]() ,
,
откуда
а=3, b=4,
![]() ,
эксцентриситет =
,
эксцентриситет =![]() .
.
Действительная ось 2а=6; мнимая ось 2b=8.
Уравнения
директрис:
![]() .
.
Уравнения
асимптот:
![]() .
.
Задача 6.
Составить
уравнение эллипса, симметричного
относительно координатных осей, зная,
что он проходит через точки М1(2;3)
и М2![]() .
.
Решение.
Учитывая
симметричность эллипса относительно
осей координат,
его каноническое уравнение будет иметь
вид
![]() , и
вместо текущих координат подставим в
это уравнение сначала координаты точки
М1,
а затем координаты точки М2.
Из получившейся системы уравнений
, и
вместо текущих координат подставим в
это уравнение сначала координаты точки
М1,
а затем координаты точки М2.
Из получившейся системы уравнений

определим параметры эллипса а и b.
Обозначив
![]() ,
,
![]() ,
,
получим следующую систему уравнений:
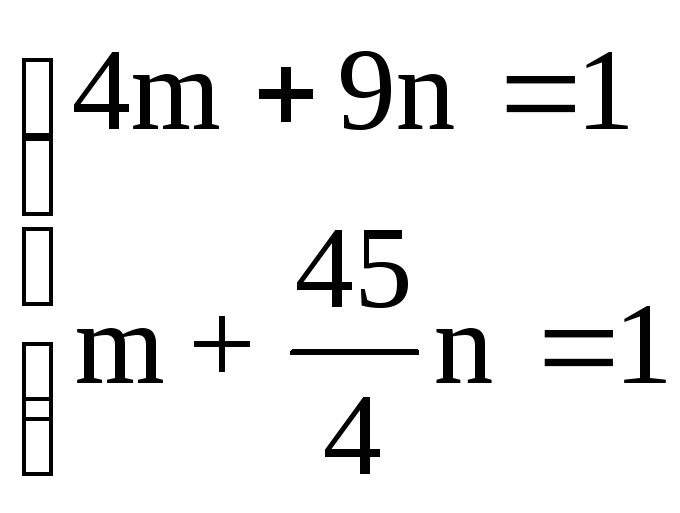 .
.
Решая ее, получим, что:
![]() ,
,
откуда а2=16, b2=12.
Следовательно, искомое уравнение эллипса будет:
![]() .
.
Задача 7.
Найти вершину, фокус, ось и директрису параболы
у = -2х2 +16х-29.
Решение.
Преобразуем данное уравнение следующим образом:
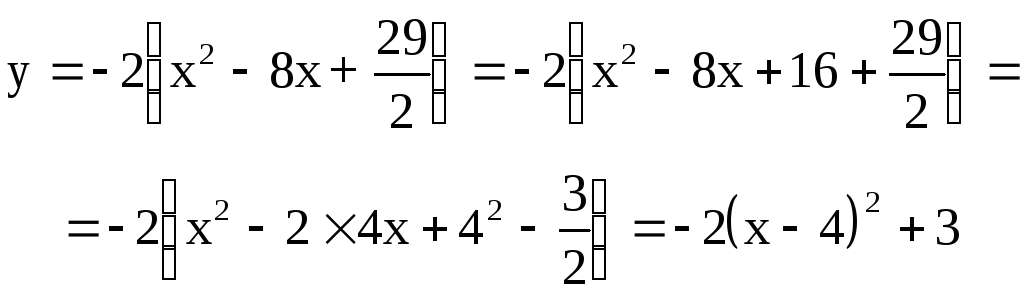
Отсюда![]() .
.
Обозначив х`= х-4 и у`= у-3, перейдем к новой системе координат O`x`y`, начало которой находится в точке O`(4;3), а оси O`x` и O`y` сонаправлены с осями Ох и Оу. В результате получим простейшее уравнение данной параболы
![]() .
.

Отсюда![]() ,
т. е.
,
т. е.
![]() .
Итак, вершина параболы находится в точке
O`(4;3); координаты фокуса
.
Итак, вершина параболы находится в точке
O`(4;3); координаты фокуса
xF
=
xO`
=
4;
![]()
т.
е. F![]() ;
уравнение оси параболы x = xO`
=
4, т. е. х-4=0; уравнение директрисы
;
уравнение оси параболы x = xO`
=
4, т. е. х-4=0; уравнение директрисы
![]() ,
т. е. 8y-25=0.
,
т. е. 8y-25=0.
Задача 8.
Уравнение
эллипса
![]() привести в полярной системе координат
к уравнению вида
привести в полярной системе координат
к уравнению вида
![]() .
.
Решение
Найдем
из данного уравнения параметры a, b, c,
затем найдем эксцентриситет
![]() и фокальный параметр эллипса
и фокальный параметр эллипса
![]() :
:
а2=4,
b2=3,
c2=1,
![]() ,
,
![]() .
.
Искомое уравнение будет иметь вид:
![]()
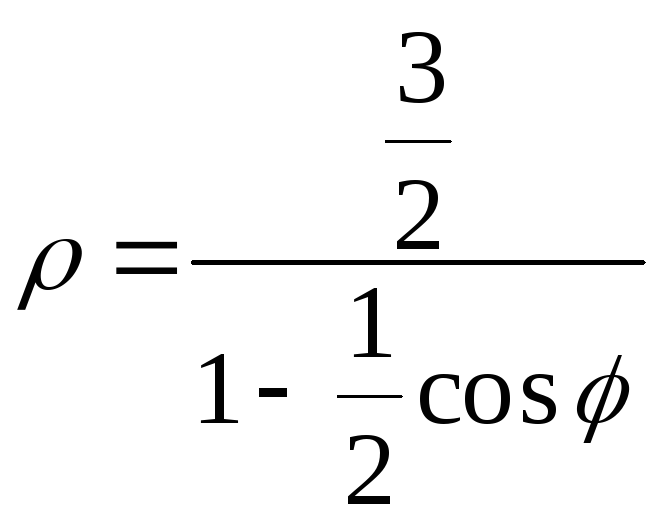 или
или
![]() .
.
Задача 9.
Данное уравнение кривой в полярных координатах
![]() .
.
Привести его к каноническому уравнению в прямоугольных координатах.
Решение.
В
данном уравнении
![]() ,
,
![]() .
Так как эксцентриситет >1,
то данное уравнение является уравнением
гиперболы, у которой b2=c2-a2.
Таким образом, данные параметры могут
быть записаны в виде системы двух
уравнений
.
Так как эксцентриситет >1,
то данное уравнение является уравнением
гиперболы, у которой b2=c2-a2.
Таким образом, данные параметры могут
быть записаны в виде системы двух
уравнений

Из этой системы находим, что а=1, с=3, b2=8. Следовательно, уравнение гиперболы имеет вид:
![]() .
.
Задача 10. Написать уравнение прямой, проходящей через две известные точки А(2;3) и В(6;-2) и вычислить длину отрезка АВ.
Решение. Уравнение прямой, проходящей через две известные точки М1(x1,y1) М2(x2,y2), имеет вид:
![]() ,
,
поэтому уравнение прямой (АВ) примет вид:
 .
.
Расстояние между точками М1 и М2 определяется по формуле
![]()
поэтому длина отрезка АВ:
![]() .
.
Задача 11. Написать уравнение высоты (BN) и вычислить ее длину в треугольнике А(6;0), В(2;-3), С(-4;9).
Решение: Уравнение пучка прямых, проходящих через точку М(x0,y0) имеет вид : y-y0=k(x-x0).
Угловой коэффициент прямой (BN) найдем из того условия, что (ВN)(АС). Условие перпендикулярности двух прямых, имеющих угловые коэффициенты k1, k2:
![]() .
.
Угловой
коэффициент прямой, проходящей через
точки М1(x1;y1)
и М2(x2;y2)
-
![]() ;
;
т.о.,
![]()
![]() и
уравнение (BN), следовательно, имеет вид:
и
уравнение (BN), следовательно, имеет вид:
![]() .
.
Для вычисления высоты BN воспользуемся формулой, определяющей расстояние d точки М0(x0;y0) до прямой, заданной уравнением Ax+By+C=0:
![]() .
.
Нам нужно определить расстояние точки В(2;-3) до прямой, идущей через точки А(6;0) и С(-4;9).
Уравнение (АС)

![]() .
.
Задача 12. Вычислить в радианах величину внутреннего угла В в треугольнике А(4;-1), В(-4;-5), С(1;10).
Решение: Для определения угла В воспользуемся формулой тангенса
|
|
угла
между двумя прямыми, имеющими угловые
коэффициенты k1
и k2:
|
В нашем случае такой прямой является (ВА) ( см.рисунок).
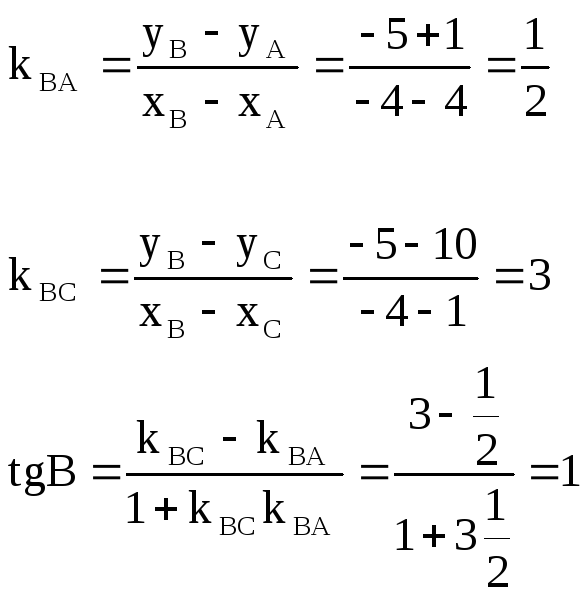
![]() .
.
Задача 13.
Написать уравнение (ВК) биссектрисы внутреннего угла треугольника с вершинами А(4;-1), В(-4;-5), С(1;5).
|
|
Решение: Воспользуемся уравнениями биссектрис углов, образованных пересечением двух прямых, заданных уравнениями: |
![]()
Уравнения таких биссектрис имеют вид:
![]()
Точка М(x;y), координаты которой удовлетворяют этому условию, равноудалена от двух данных прямых, так как в левой и правой части равенства записаны расстояния ее до этих прямых.
В нашем случае уравнения прямых (АВ) и (ВС) имеют вид:
(АВ):
![]() ,
,
(BC):
![]() .
.
Уравнения двух биссектрис угла В (внутреннего и внешнего) имеют вид:
![]() ,
что равносильно уравнениям:
,
что равносильно уравнениям:
x-2y-6=2x-y+3 или y=-x-9 (1)
x-2y-6=-(2x-y+3) или x-y-1=0(2) и y=x-1 (2)
Из уравнений (1), (2) угловые коэффициенты этих биссектрис
k=-1, k=1
Искомый угловой коэффициент должен удовлетворять неравенству:
k(BA)< k(BK) <k(BC) , (см. рисунок).
Так
как
![]()
и уравнение биссектрисы (ВК) есть x-y-1=0.
Задача 14. Составить уравнение линии, каждая точка которой вдвое дальше от прямой y+2=0, чем от точки F(-3;1).
Решение: Пусть точка М(x,y) обладает указанными свойствами:
|
|
|
Координаты x, y точки М должны удовлетворять следующему уравнению:
![]()
После возведения в квадрат и соответствующих преобразований получим уравнение:
4x2 + 24x + 3y2 - 12y + 36=0 или
4(x2 +6x +9 - 9) + 3(y2 -4y +4 -4) - 36 = 0
----------- ------------
4(x + 3)2 + 3(y-2)2 - 48 + 36 = 0
![]()
Это
уравнение эллипса с осями симметрии,
параллельными координатным осям с
центром в точке С(-3;2) и полуосями
![]() (рис. 2).
(рис. 2).
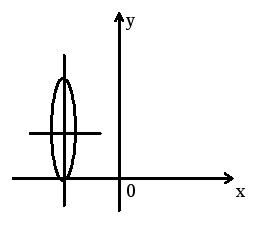
Рис. 2
Задача
15. Составить
уравнение гиперболы, симметричной
относительно координатных осей, с
фокусами на оси Ox, если уравнения ее
асимптот
![]() ,
а расстояние между директрисами
,
а расстояние между директрисами
![]() .
.
Решение:
Уравнение такой гиперболы имеет вид
![]() и для его записи необходимо вычислить
величины a и b. Так как уравнения асимптот
гиперболы имеют вид
и для его записи необходимо вычислить
величины a и b. Так как уравнения асимптот
гиперболы имеют вид
![]() ,
то имеем соотношение:
,
то имеем соотношение:
![]() (1)
(1)
Так
как расстояние между директрисами равно
![]() ,
где
- эксцентриситет, то :
,
где
- эксцентриситет, то :
![]() (2)
(2)
Кроме
того,
![]() поэтому
условие (2) можно записать так:
поэтому
условие (2) можно записать так:
![]()
Для a и b получим следующую систему:
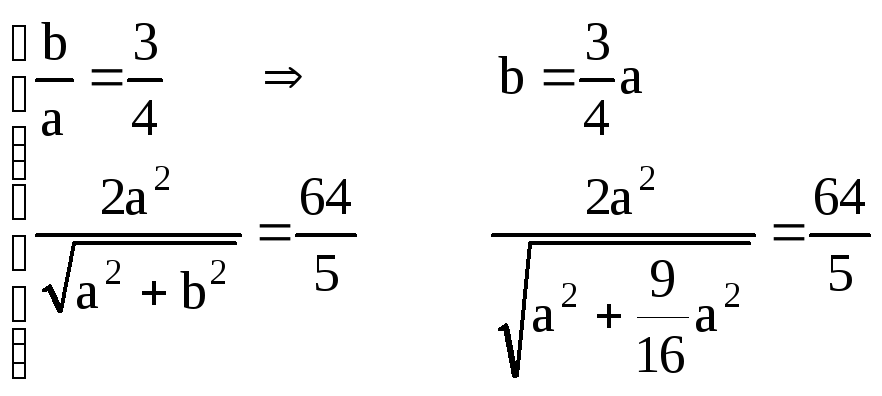
a=8, b=6 и уравнение гиперболы
![]() .
.
Задача 16 (линейное программирование).
Математическая постановка
x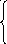 10,
10,
x20,
a11x1+a12x2b1,
a21x1+a22x2b2,
F=c1x1+c2x2max.
Графическое решение задачи линейного программирования.
Максимизировать функцию F=3x1+5x2 при ограничениях:
2x1+4x216
3x1+x29
a11=2 a12=4 b1=16
a21=3 a22=1 b2=9
c1=3 c2=5
Построим графики функций 2x1+4x2=16 и 3x1+x2=9, проходящие через точки (x1=0, x2=4; x1=8, x2=0) и (x1=0, x2=9; x1=3, x2=0) соответственно, а также x1=0 и x2=0 с областями определения x10 и x20 соответственно. В результате получим многоугольник ОABC, задающий область допустимых решений задачи.
Затем построим график функции 3x1+5x2=const., где const некоторое число, например, 15. Все точки (x1, x2) этой прямой придают целевой функции значение 15. Если теперь перемещать эту прямую параллельно самой себе, значение целевой функции будет меняться. Можно заметить, что максимальное значение из области допустимых решений целевая функция в данном случае принимает в точке пересечения прямых 2x1+4x2=16, 3x1+x2=9, задающих ограничения на область допустимых решений. Решением задачи является точка B с координатами x1=2, x2=3. Значение целевой функции в этой точке равно F=32+53=21.
Симплекс-метод решения задачи линейного программирования.
Рассмотрим применение симплекс-метода на примере задачи, решенной графическим способом.
Ф ормируем
исходную систему уравнений:
ормируем
исходную систему уравнений:
1x0-3x1-5x2=0 (0)
2x1+4x2+1x3=16 (1)
3x1+x2+1x4=9 (2)
Здесь в уравнении (0) функция F заменена на x0, а в левые части уравнений (1) и (2) добавлены фиктивные переменные x3 и x4 (x30, x40) для превращения неравенств в уравнения. Выбираем базис для начального решения. Количество переменных в базисе должно совпадать с числом уравнений, базисные переменные в системе должны присутствовать только по одному разу и коэффициенты при них равны единице. Соответственно этим условиям базисом является x0=0, x3=16 и x4=9. Тогда при этом x1=x2=0. Базисное решение совпадает с началом координат.
Первая итерация.
Выбираем переменную, которую будем вводить в базис. В данном случае это x2, так как с2>с1.
Для определения значения x2 составим таблицу.
|
№ уравнен. |
Базисная переменная |
Ее значение |
Коэффициент при x2 |
Отношение |
Min |
Решение |
|
0 |
x0 |
0 |
-5 |
- |
- |
- |
|
1 |
x3 |
16 |
4 |
16:4=4 |
4 |
x2=4 x3 |
|
2 |
x4 |
9 |
1 |
9:1=9 |
- |
- |
Вводим x2=4 в уравнение (1), а x3 выведем из базиса. Пересчитываем систему уравнений. Уравнение (1) делим на 4 (коэффициент при x2). Получаем уравнение (1’):
0.5x1+1x2+0.25x3=4. (1’).
Выражаем отсюда x2=4-0.5x1-0.25x3 и подставляем его в уравнения (0) и (2):
1x0-3x1-5(4-0.5x1-0.25x3)=0,
1x0-0.5x1+1.25x3=20, (0’)
3x1+4-0.5x1-0.25x3+1x4=9,
2.5x1-0.25x3+1x4=5. (2’)
Новая система уравнений имеет вид
1x0-0.5x1+1.25x3=20 (0’)
0.5x1+1x2+0.25x3=4 (1’)
2.5x1-0.25x3+1x4=5 (2’)
Новый базис составляют переменные x0=20, x2=4, x4=5. При этом x1=x3=0. Это решение совпадает с (.) А. Необходима еще одна итерация, так как в уравнении (0’) коэффициент при x1 отрицателен.
|
№ уравнения |
Базисная переменная |
Ее значение |
Коэффициент при x1 |
Отношение |
Min |
Решение |
|
0 |
x0 |
20 |
-0.5 |
- |
- |
- |
|
1 |
x3 |
4 |
0.5 |
4:0.5=8 |
- |
- |
|
2 |
x4 |
5 |
2.5 |
5:2.5=2 |
2 |
x1=2 x4 |
Пересчитываем систему уравнений, вводя x1=2 в уравнение (2’), для чего его делим на 2.5.
Получим уравнение (2”)
1x1-0.1x3+0.4x4=2. (2”)
Выражаем отсюда x1=2+0.1x3-0.4x4 и подставляем его в другие уравнения:
1x0-0.5(2+0.1x3-0.4x4)+1.25x3=20,
1x0+1.2x3+0.2x4=21, (0”)
0.5x0(2+0.1x3-0.4x4)+1x2+0.25x3=4,
1x2+0.3x3-0.2x4=3, (1”)
Новая система уравнений имеет вид
1x0+1.2x3+0.2x4=21, (0”)
1x2+0.3x3-0.2x4=3, (1”)
1x1-0.1x3+0.4x4=2. (2”)
Новый базис составляют переменные x0=21, x2=3, x1=2, среди которых нет фиктивных. При этом x3=x4=0. Это решение совпадает с точкой B (x1=2, x2=3, F=21) и является наилучшим, так как в уравнении (0”) нет отрицательных коэффициентов при переменных x1 и x2.
Задача 17
Транспортная задача.
В двух пунктах отправления A1 и А2 находится соответственно 20 и 30 т горючего. В пункты В1, В2, В3 требуется доставить соответственно 15, 15 и 20 т горючего. Стоимости перевозки тонны горючего из пункта A1 в пункты В1, В2, В3 составляют соответственно 5, 4 и 1 денежных единиц, а из пункта А2 4, 3, 2 соответственно. Составить оптимальный план перевозок горючего так, чтобы общая сумма транспортных расходов была наименьшей.
Решение.
Построим таблицу исходных данных:
|
|
В1 |
В2 |
В3 |
ai |
|
A1
|
5 15 |
4 5 |
1
|
20 |
|
A2 |
4 |
3 10 |
2 20 |
30 |
|
bj |
15 |
15 |
20 |
50 |
Заполнение начнем с клетки (1,1): x11=min(20,15)=15, первый столбец закрыт. Переходим к клетке (1,2): x12=min(20-15,15)=5, первая строка закрыта; далее переходим к клетке (2,2): x22=min(15-5,30)=10. Так как во второй строке оказался остаток равный 20, то переходим к заполнению клетки (2,3), куда заносим x23=20. Поскольку остатки по строке и столбцу равны нулю, опорное исходное решение построено. Этому плану соответствуют затраты в количестве F= 155+54+103+202=165 денежных единиц. Такой способ построения опорного плана называется методом Северо-Западного угла.
Получив исходное опорное решение, перейдем теперь к построению новых опорных решений, улучшающих друг друга: для этого применим метод потенциалов.
Припишем каждому пункту Ai некоторое число, условно равное стоимости ед. груза в этом пункте поставки ui. Соответственно каждому пункту потребления Bj припишем также некоторое число vj. Они называются потенциалами и связаны соотношением vj=ui+cij. Теперь можно приступить к попытке улучшения опорного решения.
Первый этап.
Если предположить, что потенциал u1=0, то можно вычислить по формуле vj=ui+cij числовые значения всех остальных. Далее следует расставить все потенциалы по соответствующим ячейкам.
Второй этап.
Проверяем возможности улучшения плана. Для этого анализируем незанятые клетки и по условию vj-uicij определяем возможности дальнейшей оптимизации опорного решения.
Если vj-ui-cij0, то резервов оптимизации решения нет, если же
vj-ui-cij>0, то план не оптимален, есть резервы и, следовательно, можно переходить к алгоритму получения нового плана.
Рассмотрим пример применения метода потенциалов для оптимизации опорного решения.
Пусть опорное решение имеет следующий вид:
|
|
В1 |
В2 |
В3 |
ai |
|
A1
|
5 15 |
4 5 |
1
|
20 |
|
A2 |
4 |
3 10 |
2 20 |
30 |
|
bj |
15 |
15 |
20 |
50 |
Оценим этот план по стоимости: F=155+54+103+202=165.
Рассчитаем потенциалы и внесем их в таблицу. Положим, что u1=0, тогда
v1=u1+c11=0+5=5,
v2=u1+c12=0+4=4,
u2=v2-c22=4-3=1,
v3=u2+c23=1+2=3
и таблица примет вид
|
|
В1 v1=5 |
В2 v2=4 |
В3 v3=3 |
ai |
|
A1 u1=0 |
5 15 |
4 5 |
1
|
20 |
|
A2 u2=1 |
4 |
3 10 |
2 20 |
30 |
|
bj |
15 |
15 |
20 |
50 |
Выполним проверку для незанятых ячеек условия vj-ui-cij0. Для ячейки А1В3 получаем v3-u1-cij0 или 3-0-10, т.е. условие не выполняется и, следовательно, есть резервы для улучшения плана. Для ячейки А1В3 v1-u2-c21 или 5-1-4=0 – условие выполняется, т.е. резервов для улучшения плана нет.
Переместив 5 единиц продукции по циклу А1В2А1В3А2В3А2В2, получим новый план:
|
|
В1 v1=5 |
В2 v2=4 |
В3 v3=3 |
ai |
|
A1 u1=0 |
5 15 |
4
|
1 5 |
20 |
|
A2 u2=1 |
4 |
3 15 |
2 15 |
30 |
|
bj |
15 |
15 |
20 |
50 |
Оценим план: F=155+51+153+152=155.
Теперь выполним проверку условия vj-ui-cij0 для ячеек А1В2 и А2В1. Для ячейки А2В1 получаем 5+1-30, т.е. условие не выполняется и, следовательно, есть резервы для улучшения плана. Для ячейки А1В2 или 2-4+00 – условие выполняется, т.е. резервов для улучшения плана нет.
Перемещая 15 единиц по контуру А1В1А1В3А2В3А2В1, получим новый план:
|
|
В1 v1=5 |
В2 v2=4 |
В3 v3=3 |
ai |
|
A1 u1=0 |
5 0 |
4 0 |
1 20 |
20 |
|
A2 u2=1 |
4 15 |
3 15 |
2 0 |
30 |
|
bj |
15 |
15 |
20 |
50 |
Оцениваем план: F=201+154+153=125.
Дальнейшая проверка показывает, что условие vj-ui-cij0 для А1В2 и А2В3 выполняется, следовательно, резервов для улучшения плана нет.
Задача 18 (динамическое программирование).
Производственное объединение, имеющее четыре филиала в разных городах, желает распределить ресурсы в 10 млн руб. так, чтобы получить наибольшую прибыль. Специалисты объединения изучили состояние рынка в каждой зоне и определили кривые математического ожидания прибыли как функции полных капитальных вложений:
|
Капитальные вложения А, млн руб. |
Математическое ожидание прибыли по зонам |
|||
|
1 |
2 |
3 |
4 |
|
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0.28 |
0.25 |
0.15 |
0.20 |
|
2 |
0.45 |
0.41 |
0.25 |
0.33 |
|
3 |
0.65 |
0.55 |
0.40 |
0.42 |
|
4 |
0.78 |
0.65 |
0.50 |
0.48 |
|
5 |
0.90 |
0.75 |
0.62 |
0.53 |
|
6 |
1.02 |
0.80 |
0.73 |
0.56 |
|
7 |
1.13 |
0.85 |
0.82 |
0.58 |
|
8 |
1.23 |
0.88 |
0.90 |
0.60 |
|
9 |
1.32 |
0.90 |
0.96 |
0.60 |
|
10 |
1.38 |
0.90 |
1.00 |
0.60 |
Решение.
Задача сводится к перебору всех разбиений 10 на четыре группы из целых чисел: (10,0,0,0); (9,1,0,0); (9,0,1,0); (9,0,0,1); … (8,1,1,0); (8,1,0,1); (8,0,1,1); (8,2,0,0); … и т.д. Всего 286 комбинаций. Можно вычислить доходы, соответствующие каждой комбинации, и выбрать наибольший. Таким образом, имеем комбинаторную задачу. Применим для ее решения метод динамического программирования. Обозначим функции дохода для зон 1, 2, 3 и 4 соответственно f1(x), f2(x), f3(x) и f4(x). Примем F1,2(A)– оптимальное распределение, когда А вкладывается в зоны 1 и 2 вместе; F1,2,3(A) – 1, 2 и 3 вместе; F1,2,3,4(A) – оптимальное распределение, когда А вкладывается во все четыре зоны вместе.
Таким образом, чтобы определить F1,2(2), надо вычислить
f1(0)+ f2(2) = 0.00+0.41=0.41;
f1(1)+ f2(1)= 0.28+0.25=0.53;
f1(2)+ f2(0)= 0.45+0.00=0.45,
так что F1,2(A)=0.53.
Вычисляем
таким образом значения F1,2(0);
F1,2(1);
F1,2(2);
F1,2(3);
…; F1,2(20),
что дает таблицу
![]()
|
А, млн руб. |
f1(x) |
f2(x) |
F1,2(A) |
Распределение А по зонам 1 и 2, млн руб. |
|
0 |
0 |
0 |
0 |
(0.0) |
|
1 |
0.28 |
0.25 |
0.28 |
(1.0) |
|
2 |
0.45 |
0.41 |
0.53 |
(1.1) |
|
3 |
0.65 |
0.55 |
0.70 |
(2.1) |
|
4 |
0.78 |
0.65 |
0.90 |
(3.1) |
|
5 |
0.90 |
0.75 |
1.06 |
(3.2) |
|
6 |
1.02 |
0.80 |
1.20 |
(3.3) |
|
7 |
1.13 |
0.85 |
1.33 |
(4.3) |
|
8 |
1.23 |
0.88 |
1.45 |
(5.3) |
|
9 |
1.32 |
0.90 |
1.57 |
(6.3) |
|
10 |
1.38 |
0.90 |
1.68 |
(7.3) |
Таблица позволяет определить политики, соответствующие оптимальному доходу при данных капитальных вложениях. Например, если в зоны 1 и 2 вложить 4 млн руб., то в зону 1 следует вложить 3 млн руб., а в зону 2 – 1 млн руб.
Продолжим исследование поиском F1,2,3(A) , т.е. поиском оптимальной комбинации, когда капитальные вложения вкладываются в зоны 1, 2 и 3, причем
![]()
|
А, млн руб. |
F1,2(x) |
f3(x) |
F1,2,3(A) |
Распределение А по зонам, млн руб. |
|
|
1 и 2 |
1, 2 и 3 |
||||
|
0 |
0 |
0 |
0 |
(0.0) |
(0,0,0) |
|
1 |
0.28 |
0.15 |
0.28 |
(1.0) |
(1,0,0) |
|
2 |
0.53 |
0.25 |
0.53 |
(1.1) |
(1,1,0) |
|
3 |
0.70 |
0.40 |
0.70 |
(2.1) |
(2,1,0) |
|
4 |
0.90 |
0.50 |
0.90 |
(3.1) |
(3,1,0) |
|
5 |
1.06 |
0.62 |
1.06 |
(3.2) |
(3,2,0) |
|
6 |
1.20 |
0.73 |
1.21 |
(3.3) |
(3,2,1) |
|
7 |
1.33 |
0.82 |
1.35 |
(4.3) |
(3,3,1) |
|
8 |
1.45 |
0.90 |
1.48 |
(5.3) |
(4,3,1) |
|
9 |
1.57 |
0.96 |
1.60 |
(6.3) |
(5,3,1); (3,3,3) |
|
10 |
1.68 |
1.00 |
1.73 |
(7.3) |
(3,3,3) |
Продолжим вычисления, определяя
![]()
|
А, млн руб. |
F1,2,3(x) |
f4(x) |
F1,2,3,4(A) |
Распределение А по зонам, млн руб. |
|
|
1,2 и 3 |
1, 2, 3 и 4 |
||||
|
0 |
0 |
0 |
0 |
(0,0,0) |
(0,0,0,0) |
|
1 |
0.28 |
0.15 |
0.28 |
(1,0,0) |
(1,0,0,0) |
|
2 |
0.53 |
0.25 |
0.53 |
(1,1,0) |
(1,1,0,0) |
|
3 |
0.70 |
0.40 |
0.73 |
(2,1,0) |
(1,1,0,1) |
|
4 |
0.90 |
0.50 |
0.90 |
(3,1,0) |
(3,1,0,0) (2,1,0,1) |
|
5 |
1.06 |
0.62 |
1.10 |
(3,2,0) |
(3,1,0,1) |
|
6 |
1.21 |
0.73 |
1.26 |
(3,2,1) |
(3,2,0,1) |
|
7 |
1.35 |
0.82 |
1.41 |
(3,3,1) |
(3,2,1,1) |
|
8 |
1.48 |
0.90 |
1.55 |
(4,3,1) |
(3,3,1,1) |
|
9 |
1.60 |
0.96 |
1.68 |
(5,3,1); (3,3,3) |
(4,3,1,1); (3,3,1,2) |
|
10 |
1.73 |
1.00 |
1.81 |
(3,3,3) |
(4,3,1,2) |
Можно убедиться, что те же результаты имеют место при любом ином порядке вычислений: F3,1(A), F3,1,2(A), F3,1,2,4(A) и т.п., результаты расчетов оформим в виде таблицы:
|
А, млн руб. |
Распределение А по зонам |
Оптимальная прибыль |
|||
|
1 |
2 |
3 |
4 |
||
|
1 |
1 |
0 |
0 |
0 |
0.28 |
|
2 |
1 |
1 |
0 |
0 |
0.53 |
|
3 |
1 |
1 |
0 |
1 |
0.73 |
|
4 |
3 2 |
1 1 |
0 0 |
0 1 |
0.90 0.90 |
|
5 |
2 |
1 |
0 |
1 |
1.10 |
|
6 |
3 |
1 |
0 |
1 |
1.26 |
|
7 |
3 |
2 |
0 |
1 |
1.41 |
|
8 |
3 |
3 |
1 |
1 |
1.55 |
|
9 |
4 3 |
3 3 |
1 1 |
1 2 |
1.68 1.68 |
|
10 |
4 |
3 |
1 |
2 |
1.81 |
Таким образом, оптимальное распределение 10 млн руб. в четыре зоны следующее: (4,3,1,2). При этом гарантируется максимальная прибыль 1.81.
Интересно отметить, что попутно решены задачи оптимального распределения любого числа из 10 в две, три и четыре зоны.

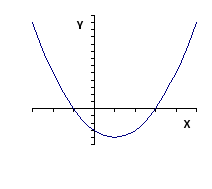
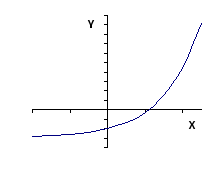

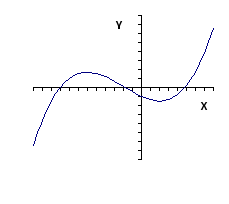
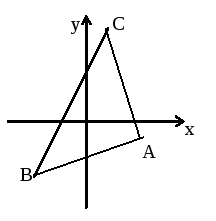
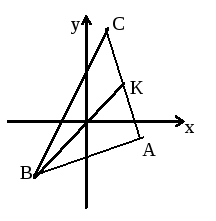
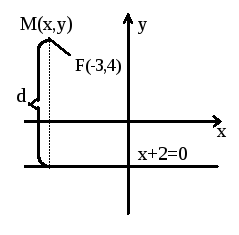 Рис.
1
Рис.
1