2. Основные теоретические положения математического анализа

1. Теория множеств

Основные понятия

Множество есть исходное, начальное (а, следовательно, и неопределяемое) понятие. Можно лишь сказать, что множество есть собрание объектов, при этом не будем уточнять, какие собрания объектов являются множествами. Объекты этого собрания называются элементами множества.

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если множество состоит из n элементов, то это обозначают следующим образом:

.

Часто приходится сталкиваться с другими, неконечными, или, как принято говорить, бесконечными множествами. Таковы, например, множества всех натуральных чисел, всех нечетных чисел и т.д.

К числу конечных множеств мы будем относить и пустое множество, т.е. множество, не содержащее ни одного элемента; число элементов пустого множества есть нуль. Такое множество обозначим символом .

Если элемент x принадлежит множеству А, то пишут xA.

Запись , или xA, означает, что x не есть элемент множества А.

Запись  (или ) означает, что каждый элемент множества А является элементом множества В или, другими словами, множество А есть подмножество множеств В (или множество А включено в множество В).

Два множества называются равными, если они состоят из одних и тех же элементов: запись А=В.

Если А есть подмножество В, причем множество А не совпадает с множеством В, то пишут    или   .

Если множество А не принадлежит множеству В, то пишут   , . Знаки      называются знаками включения.

Разберем некоторые понятия математической логики. Прежде всего, что такое математическая логика?

Математическая логика – наука о законах логического вывода.

В математической логике под предложением понимают то же самое, что вкладывают в смысл этого термина в грамматике любого естественного языка.

Высказыванием называется предложение, о котором имеет смысл говорить, что оно истинно или ложно. Каждое высказывание либо истинно, либо ложно. Истинному высказыванию будем ставить в соответствие единицу, а ложному – логический ноль (1;0).

Пример: (10=15)=0 (высказывание “10 равно 15” - ложно)

(5>-1)=1 (высказывание “5 больше -1” - истинно).

Будем обозначать высказывания буквами какого-либо алфавита:

X, Y,L,.........; А, В,......

Высказывательная форма – это выражение, содержащее одну или несколько переменных и становящееся высказыванием при подстановке чисел или элементов каких-либо множеств вместо своих переменных.

Кванторы

Иногда удобно представить некоторые словесные выражения посредством символов.

 - каково бы ни было, для любого (квантор всеобщности).

 - существует (квантор существования).

– для любого x выполняется предложение .

Символом “:” будем обозначать следующую группу слов: “такое, что”, “удовлетворяет условию”, “выполняется”.

Отрицание высказываний, содержащих кванторы

Отрицание под знаком  или  превращает его, соответственно, в знак  или  и переносится на свойство, стоящее после двоеточия.

Пример 1.

Пусть имеем высказывание: (x x   (для любого x из множества А имеет место неравенство x  ). Если высказываемое утверждение не имеет места, то, следовательно, неравенство x   выполняется не для каждого x, значит существует элемент x, для которого неравенство x   не выполняется.

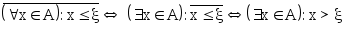
Пример 2.

Используя закон Моргана, построить отрицание предела функции f(x) в точке x=а.

Сформулируем определение предела функции f(x) в точке x=a по Коши с использованием введенной символики:

.

Здесь на языке алгебры записано: вещественное число b называется пределом функции f(x) в точке x=a, если для любого вещественного положительного числа ε найдется вещественное положительное число , что для всех значений аргумента x из области определения таких, что, если выполнены неравенства , будет следовать неравенство .

Операции над множествами

Объединение АВ множеств А и В

Множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из данных множеств, называется объединением множеств А и В. Указанное определение легко распространяется на случай трех и более множеств:

АВ заштриховано на диаграмме.

Пример 1.

А1,2,3,4,5,

В1,2,

АВ=1,2,3,4,5.

Множество АВ по определению не содержит неразличимых элементов и, следовательно, элементы 1 и 2, входящие в множества А и В, входят в АВ один раз.

Пересечение АВ множеств А и В есть множество элементов, принадлежащих и А и В.

АВ заштриховано на диаграмме.

Пример 2.

А1,2,3,4,5; В1,2

АВ=1,2

Два множества А и В называются непересекающимися, если АВ=Ø.

Разность А\В множеств А и В

Разностью множеств А и В называется совокупность тех элементов А, которые не содержатся в В.

А\В заштриховано на диаграмме.

Пример 3.

А=1,2,3,4,5, В=1,2

А\В=3,4,5.

Взаимно однозначное соответствие и эквивалентность множеств

Если каждому элементу множества А сопоставлен единственный элемент множества В, и при этом всякий элемент множества В сопоставляется одному и только одному элементу множества А, то говорят, что между множествами А и В установлено взаимно однозначное соответствие.

Множества, между которыми установлено взаимно однозначное соответствие, называются эквивалентными. Это записывается следующим образом: А~В. Если два множества эквивалентны, то говорят, что они равномощны, или имеют одну и ту же мощность.

Прямое произведение двух множеств

Пусть имеются два множества А и В и пусть аА, bB. Совокупность всевозможных упорядоченных пар (а,b) составляет новое множество, называемое прямым произведением А и В. Прямое произведение обозначается АВ.

Вещественные числа и их изображение на числовой оси. Основные свойства рациональных чисел

Основным понятием математики являются числа натурального ряда:

которые появились в результате счета предметов.

Целые числа:

Рациональным числом называется число, представимое в виде отношения двух целых чисел (q0; p и q - целые числа).

Отметим при этом, что одно и то же рациональное число представимо в виде отношения различных целых чисел . Множество всех рациональных чисел будем обозначать через Q, тогда

В курсе элементарной математики вводились определения операций сложения и умножения рациональных чисел, давалось правило сравнения этих чисел, доказывались простейшие свойства.

Поэтому перечислим без доказательства основные свойства рациональных чисел, вытекающие из соответствующих свойств целых чисел.

Главную роль среди свойств играют три правила:

- правило сравнения;

- правило образования сумм;

- правило образования произведения.

I. Правило сравнения: любые два рациональные числа а и b связаны одним и только одним из трех знаков   , причем если аb, то b а.

Правило сравнения рациональных чисел формулируется так: два неотрицательных рациональных числа связаны тем же знаком, что и два целых числа ; два неположительных рациональных числа а и b связаны тем же знаком, что и два неотрицательных числа b и а ; если а - неотрицательное, а b - отрицательное число, то аb.

Правило сравнения обладает следующим свойством:

1. (из аb и bс) ас (свойство транзитивности знака );

(из а=b и b=с) а=с (свойство транзитивности знака =).

II. Правило образования сумм.

Существует правило, посредством которого любым двум рациональным числам а и b ставится в соответствие определенное рациональное число с, называемое их суммой и обозначаемое символом с=а+b.

Правило образования суммы рациональных чисел определяется формулой . Операция нахождения суммы называется сложением.

Правило сложения рациональных чисел обладает следующими свойствами:

2. а+b=b+а (коммутативность, или переместительное свойство);

3.(а+b)+c=а+(b+c) (ассоциативность, или сочетательное свойство);

4.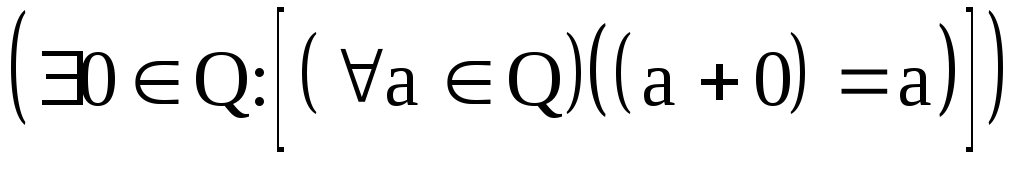 (особая роль нуля);

5.; число а¹ называется противоположным для числа а.

III. Правило образования произведения.

Существует правило, посредством которого любым двум рациональным числам а и b ставится в соответствие определенное рациональное число с, называемое их произведением и обозначаемое символом с=аb.

Правило образования произведения рациональных чисел

определяется формулой .

Операция нахождения произведения называется умножением. Свойства правила умножения рациональных чисел:

6. (переместительное свойство);

7. (сочетательное свойство);

8. 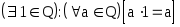(особая роль единицы);

9. рациональное число а^-1называется обратным рациональному числу а.

Свойство, связывающее правила сложения и умножения:

10. (распределительное свойство умножения относительно суммы).

Свойства, связывающие знак  со знаком сложения и умножения:

11.

12.

Последнее свойство, называемое аксиомой Архимеда, формулируется следующим образом.

Каково бы ни было рациональное число а, можно число 1 повторить слагаемым столько раз, что полученная сумма превзойдет а.

Из вышеперечисленных основных свойств рациональных чисел могут быть получены как следствие все другие алгебраические свойства этих чисел, относящиеся как к арифметическим действиям, так и к сочетанию равенств и неравенств.