Равнобочная гипербола

Возьмем каноническое уравнение гиперболы

.

В случае, когда а=b, уравнение гиперболы имеет вид

или

х² - у² = а² (14)

Гипербола, у которой полуоси а и b равны, называется равнобочной гиперболой. Уравнение (14) называется уравнением равнобочной гиперболы. Так как основной прямоугольник этой гиперболы является квадратом, то асимптоты равнобочной гиперболы будут перпендикулярны друг другу (рис. 5)

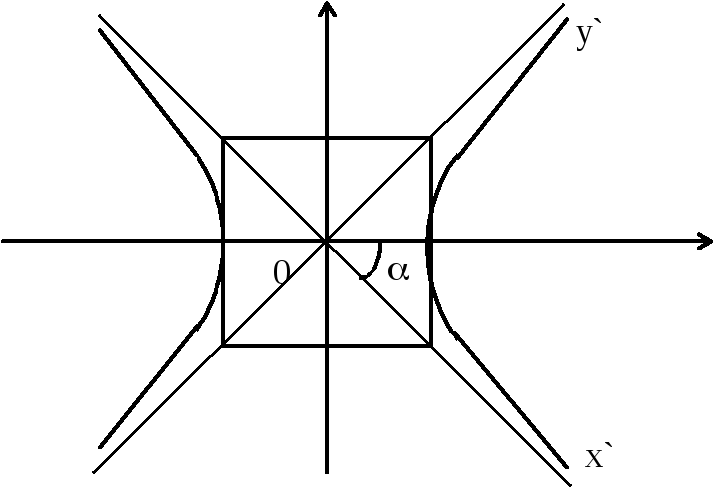
Рис. 5

Сопряженная гипербола

Рассмотрим уравнение

. (15)

Представим уравнение (15) в следующем виде:

. (16)

Очевидно, что уравнение (16) представляет собой уравнение гиперболы, у которой действительной осью является ось ординат, а мнимой – ось абсцисс.

Построим основной прямоугольник, проведем асимптоты и построим гиперболу (15). Далее в той же системе координат построим (пунктиром) (рис. 6) гиперболу

Рис. 6

Очевидно, что гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Выведем теперь уравнение гиперболы, асимптотами которой служат оси координат.

Уравнение равнобочной гиперболы, для которой координатные оси ОХ и OY являются асимптотами, будет иметь вид:

ху = с

или

.

Эксцентриситет и фокальные радиусы гиперболы

Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине ее действительной оси:

или .

Так как у гиперболы с>a, то эксцентриситет гиперболы больше единицы. Эксцентриситет характеризует отношение сторон основного прямоугольника, а следовательно, и форму самой гиперболы.

Парабола Определение параболы и ее уравнение

Параболой называется геометрическое место точек на плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус).

Для вывода уравнения параболы за ось ОХ возьмем прямую, проходящую через фокус перпендикулярно директрисе. За положительное направление оси абсцисс возьмем направление от директрисы к фокусу (рис.7).

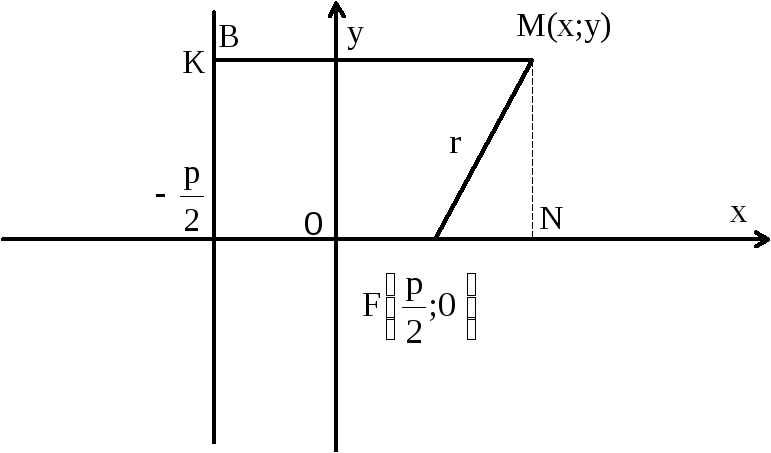
Рис. 7

За начало координат возьмем точку 0, которая делит пополам отрезок от директрисы до фокуса. Длину этого отрезка, который называется параметром параболы, обозначим через Р. Фокус F будет иметь координаты , а координаты точки оси ОХ, через которую проходит директриса, будут .

Возьмем произвольную точку М(х;у), лежащую на параболе, соединим ее прямой с точкой F, а затем опустим из точки М на директрису перпендикуляр МК. Длина отрезка, соединяющего точку М(х;у) параболы с фокусом, называется фокальным радиусом этой точки и обозначается через r (рис. 7).

Согласно определению параболы:

FM = KM (17)

Определяя FM и КМ по формуле расстояния между двумя точками, получим:

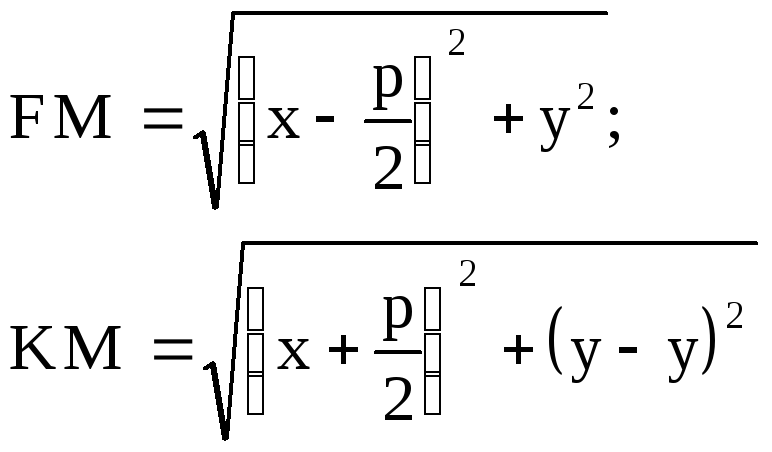
Следовательно,

(18)

Уравнению (18) будут удовлетворять координаты каждой точки параболы.

Приведем уравнение параболы к более удобному виду, для чего возведем обе части равенства (18) в квадрат:

Откуда

у² = 2рх (19)

Уравнение (19) называется каноническим уравнением параболы. Сопоставляя равенства (17) и (18), можно выразить фокальный радиус точки М(х;у) параболы через абсциссу этой точки:

. (20).