Некоторые дополнительные предложения и примеры

1. В аналитической геометрии часто требуется составить уравнение прямой, зная две ее точки. Решим эту задачу в общем виде, считая данными две произвольные точки:

М₁(x₁;y₁; z₁) и М₂(x₂;y₂; z₂).

Для решения задачи достаточно заметить, что в качестве направляющего вектора рассматриваемой прямой можно взять вектор ; отсюда m=x₂ - x₁; n=y₂ - y₁; p=z₂ - z₁, окончательно получим

.

Это и есть искомые (канонические) уравнения прямой, проходящей через две данные точки: М₁(x₁;y₁; z₁) и М₂(x₂;y₂; z₂).

2. Решим также в общем виде задачу: составить уравнение плоскости, проходящей через три различные точки: М₁(x₁;y₁; z₁); М₂(x₂;y₂; z₂); М₃(x₃;y₃; z₃).

Обозначим через x, y, z координаты произвольной точки М пространства и рассмотрим три вектора:

,

,

.

Точка М лежит на плоскости М₁М₂М₃ в том и только в том случае, когда векторы , и компланарны; условием компланарности этих трех векторов является равенство нулю их смешанного произведения или равенство нулю определителя третьего порядка, составленного из их координат.

В нашем случае имеем:

.

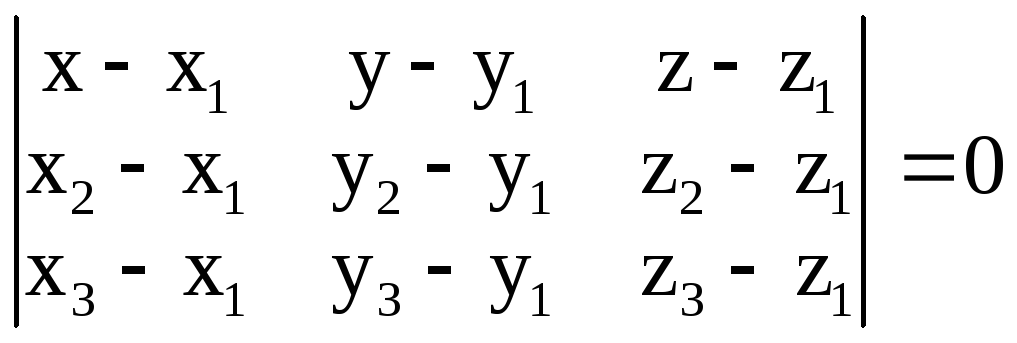Это и есть искомое уравнение плоскости, проходящей через точки М₁, М₂, М₃, так как ему удовлетворяют координаты x, y, z точки М в том и только в том случае, когда она лежит в этой плоскости.

3. Угол между двумя прямыми.

Углом между двумя прямыми в пространстве называют любой из углов, образованных двумя прямыми, проведенными из одной точки параллельно данным прямым. Если прямые параллельны, то угол между ними считается равным нулю или .

Пусть даны уравнения двух прямых:

Обозначим угол между прямыми через , а угол между их направляющими векторами и - через . При этом

(1)

Так как = или = - , то cos=cos. Следовательно,

(2)

или в координатной форме:

(3)

Формулы (2) и (3) являются формулами для определения угла между двумя прямыми в пространстве.

4. Условия параллельности и перпендикулярности двух прямых в пространстве.

Для того, чтобы две прямые были параллельны, необходимо и достаточно, чтобы их направляющие векторы и были коллинеарны, т.е. соответствующие координаты векторов и были пропорциональны:

(4)

Условие (4) является условием параллельности двух прямых в пространстве.

Для того, чтобы прямые были перпендикулярны между собой, необходимо и достаточно, чтобы направляющие их векторы и были ортогональными.

Условие ортогональности двух векторов и :

m₁m₂+n₁n₂+p₁p₂=0 (5)

является условием перпендикулярности двух прямых в пространстве.

Пример. Найти уравнение прямой, проходящей через точку М(3; 2; -1) перпендикулярно двум прямым:

; .

Составим уравнение любой прямой, проходящей через точку М:

(6)

Используя условие перпендикулярности искомой прямой к прямой а₁, а затем к прямой а_2, получим

2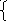m-3n+5p=0,

4m+n-2p=0.

Из этой однородной структуры линейных уравнений с неизвестными m, n, p найдем отношения неизвестных:

.

Подставляя в уравнения прямой (6) вместо m, n, p пропорциональные им величины, получим искомые уравнения:

.

5. Углом между прямой и плоскостью называют любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Пусть дано уравнение плоскости П:

Ax+By+Cz+D=0

и уравнение прямой :

.

={А; В; С} – нормальный вектор плоскости;

={m; n; p} – направляющий вектор прямой.

Обозначим угол между векторами и через , а угол между плоскостью П и прямой - через . Найдем косинус угла  между векторами и :

.

При этом sin=cos. Следовательно,

или, в координатной форме,

.

Для того, чтобы плоскость П была параллельна прямой , необходимо и достаточно, чтобы векторы ={А; В; С} и ={m; n; p} были ортогональны между собой.

Условие ортогональности двух векторов и может быть записано как равенство нулю их скалярного произведения:

()=0

или в координатной форме:

Am+Bn+Cp=0.

Для того, чтобы прямая была перпендикулярна плоскости П, необходимо и достаточно, чтобы вектор был коллинеарен вектору .

Условие коллинеарности двух векторов и может быть записано как равенство нулю их векторного произведения:

()=0

или

.

Пример. Составить уравнение плоскости П, проходящей через точку М(-1; 2; -3) параллельно двум прямым:

,

.

Напишем уравнение связки плоскостей с центром в точке М:

A(x+1)+B(y-2)+C(z+3)=0.

Используем условие параллельности плоскости П и прямой , а затем и прямой :

3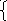А+4В+5С=0

2А-3В+С=0

Из этой системы однородных уравнений определим отношения коэффициентов А, В, С и затем в уравнение (4) вместо коэффициентов А, В, С подставим пропорциональные им величины:

;

11(x+1)+13(y-2)+17(z+3)=0;

11x+13y+17z+36=0.

6. Пучок плоскостей.

Через всякую прямую в пространстве можно провести бесчисленное множество плоскостей. Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей.

Пусть дано уравнение прямой как линии пересечения двух плоскостей:

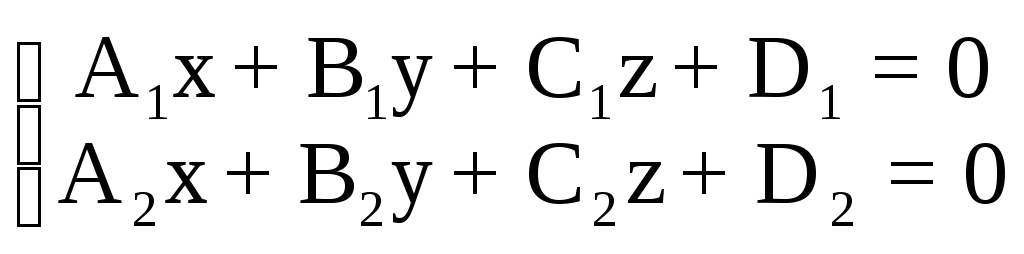(7)

Составим уравнение:

A₁x+B₁y+C₁z+D₁+(A₂x+B₂y+C₂z+D₂)=0, (8)

где  – произвольное число. При любом  это уравнение первой степени, кроме того, при любом  это уравнение определяет плоскость, проходящую через прямую (7).

Действительно, если точка М₀ принадлежит прямой (7), то:

и, следовательно

A₁x₀+B₁y₀+C₁z₀+D₁+(A₂x₀+B₂y₀+C₂z₀+D₂)=0.

Уравнение (8) называется уравнением пучка плоскостей, проходящих через прямую (7).

Уравнение (8) дает любую плоскость пучка, за исключением плоскости

A₂x+B₂y+C₂z+D₂=0.

Пример. Найти проекцию прямой

На плоскость 3x-4y+z-8=0 (П).

Составим уравнение пучка плоскостей, проходящих через прямую (9):

2x-3y+4z-1+(x+5y-2z+3)=0 (10)

или (2+)x+(5-3)y+(4-2)z+(3-1)=0.

Определим , используя условие перпендикулярности плоскостей: 3(2+)-4(5-3)+(4-2)=0. Откуда . Подставив значение в уравнение (10), найдем уравнение проектирующей плоскости:

,

Уравнения искомой проекции можно записать как уравнения линии пересечения плоскостей:

Пример. Составить уравнение плоскости, проходящей через прямую параллельно прямой .

Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

3x+2y+5z+6+(x+4y+3z+4)=0 (_*)

Преобразуем это уравнение: (3+)x+(2+4)y+(5+3)z+(6+4)=0. Используя условие параллельности прямой и плоскости получим: 3(3+)+2(2+4)-3(5+3)=0. Отсюда =1. Подставляя найденное значение  в уравнение (_*), найдем: 4x+6y+8z+10=0 или 2x+3y+4z+5=0.

Пример. Найти расстояние от точки М(1; 2; 3) до прямой

.

Решение. Проведем через М плоскость П, перпендикулярную к данной прямой и найдем точку Р, где эта плоскость пересекает данную прямую. Искомое расстояние от точки М до данной прямой будет равно расстоянию от точки М до точки Р.

Искомое уравнение плоскости П можно записать в виде:

A(x-1)+B(y-1)+C(z-1)=0;

эта плоскость должна быть перпендикулярна к данной прямой. По условию перпендикулярности прямой к плоскости имеем:

.

Выбирая здесь множитель пропорциональности для простоты равным единице, находим А=2, В=5, С=-2. Итак, плоскость имеет уравнение 2(x-1)+5(y-1)-2(z-1)=0 или 2x+5y-2z=0.

Теперь мы должны найти точку Р, в которой эта плоскость пересекается с данной прямой. Для этого нужно уравнение данной прямой решить совместно с найденным уравнением плоскости П:

.

Отсюда x=2t+11, y=5t+18, z=4-2t. Подставляя эти уравнения в уравнение найденной плоскости 2x+5y-2z-5=0, получим:

4t+22+25t+90+4t-8-5=0;

33t=-99;

t=-3.

Координаты точки Р будут равны x=5, y=3, z=10.

Искомое расстояние d от точки М до данной прямой, равное расстоянию между точками М и Р, найдется по формуле нахождения расстояния между двумя точками:

Пример. Определить условие, при котором две прямые

,

лежат на одной плоскости.

Решение. Пусть ={m₁; n₁; p₁} и ={m₂; n₂; p₂} - направляющие векторы данных прямых, М₁(a₁; b₁; c₁) и М₂(a₂; b₂; c₂) - точки, принадлежащие прямым и . Вектор ={a₂-a₁; b₂-b₁; c₂-c₁} и направляющие векторы прямых и компланарны в том и только в том случае, когда прямые и лежат в одной плоскости. Условием компланарности трех векторов является равенство нулю их смешанного произведения: =0, что в координатной записи может быть представлено в следующем виде:

.
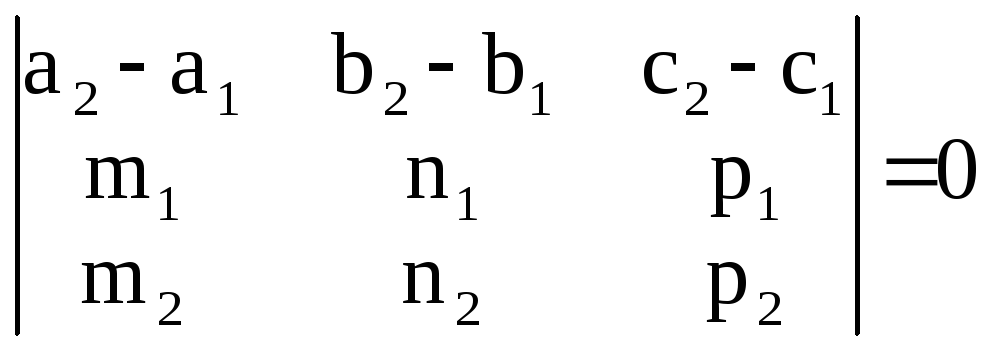