5. Интегрирование функций

Пусть для любого значения аргумента x задана скорость f(x) изменения некоторой функции F(x). Известно значение y₀=F(x₀). Найдем эту функцию.

Поскольку f(x) является производной функции y=F(x), то задача сводится к отысканию по данной функции f(x) такой функции F(x), производная F'(x) которой равна f(x).

Таким образом, мы приходим к математическим понятиям первообразной и неопределенного интеграла. Первообразной функции f(x) называется такая функция F(x), производная F'(x) которой равна f(x).

Очевидно, что если функция F(x) является первообразной функции f(x), то и функция F(x) + C, где C – любая постоянная, также является первообразной функции f(x) (ибо производная постоянной C равна нулю).

Совокупность всех первообразных одной и той же функции f(x) называется неопределенным интегралом от функции f(x) и обозначается символом ∫f(x)dx.

Следовательно, если F(x) – одна из первообразных функции f(x), то

∫f (x) dx = F (x) + C.

Для определения постоянной C воспользуемся тем, что y=y₀, когда x=x_0, т.е. y₀ = F(x₀) + C, откуда C = y₀ - F(x₀). Таким образом, интересующая нас функция имеет вид

y = F(x) + y₀ - F(x₀).

Основными свойствами неопределенного интеграла являются следующие:

d∫f(x)dx = f(x)dx;

∫dF(x) = F(x) + C;

∫[f(x)±g(x)]dx = ∫f(x)dx±∫g(x)dx;

∫ [Af (x)] dx = A∫f (x) dx, (A=const).

Ранее мы выписали таблицу производных элементарных функций. Учитывая, что каждая формула F'(x) = f(x) этой таблицы приводит к соответствующей формуле ∫f(x)dx = F(x) + C, мы получим следующую таблицу неопределенных интегралов:

п/п	f (x)	∫f (x) dx = F (x) + C
1	xα	x α+1/(α+1) + C, (α≠-1)
2	1/x	ln|x| + C
3	ax	ax/lna + C
4	sin x	-cos x + C
5	cos x	sin x + C
6	c	сx + C

Данная таблица вместе с правилами интегрирования представляет собой важный вычислительный аппарат той части математического анализа, которую обычно называют интегральным исчислением.

Однако для вычисления многих неопределенных интегралов этого аппарата недостаточно. Возникает проблема существования первообразной (и неопределенного интеграла) у произвольной функции f(x), непрерывной в каждой точке x. Отметим, что существуют непрерывные (в каждой точке x) функции (например, y = cosx²), первообразные которых существуют, но не могут быть представлены с помощью конечного числа операций сложения, вычитания, умножения, деления и образования сложных функций от простейших элементарных функций, перечисленных ранее.

6. Определенный интеграл, основные теоремы

Пусть функция f(x) имеет все неотрицательные значения (см. рис. 3). Требуется вычислить площадь, ограниченную отрезком графика функции на интервале изменений аргумента от x=a до x=b.

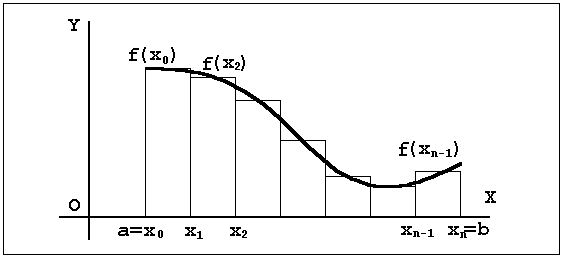
Рис. 3

Для решения задачи разобьем рассматриваемый интервал значений аргумента на малые промежутки, ограниченные точками a=x_o<x₁<x₂<...x_n=b. Естественно считать, что на каждом промежутке от x_k-1 до x_k значение функции f(x) меняется мало. Поэтому приближенно значение функции на указанном промежутке можно считать постоянным и равным, например, f(x_k). В таком случае площадь, ограниченная функцией f(x) на промежутке изменения аргумента ∆x_k=x_k -x_k-1, приближенно равна f(x_k)∆x_k, а полная площадь _aS^b на интервале от a до b приблизительно равна

_aS^b ≈ f(x₁)∆x₁ + f(x₂)∆x₂ + ... + f(x_n)∆x_n.

Естественно ожидать, что при уменьшении всех промежутков ∆x_k мы будем получать все более и более точное значение площади _aS^b. Точное значение площади мы получим, перейдя в сумме к пределу при стремлении всех ∆x_k к нулю (при этом количество слагаемых будет возрастать). Употребляя символ предела, мы можем записать следующую формулу:

_aS^b = lim_∆xk→0 {f(x₁)∆x₁ + f(x₂)∆x₂ + ... + f(x_n)∆x_n}.

В математике предел данной суммы называется определенным интегралом от функции f(x) в пределах от a до b и обозначается символом

Приближенная сумма представляет собой сумму площадей прямоугольников, основаниями которых служат отрезки ∆x_k, а высотами – f(∆x_k). Иными словами, эта сумма равна площади изображенной на рис.3 ступенчатой фигуры. Естественно ожидать, что при стремлении к нулю длин всех отрезков ∆x_k площадь указанной ступенчатой фигуры будет стремиться к площади заштрихованной фигуры, лежащей под графиком функции y = f(x) на отрезке от a до b. Эту криволинейную фигуру часто называют криволинейной трапецией. Таким образом, определенный интеграл равен площади указанной криволинейной трапеции.

Рис. 4

Обозначим через F(x) определенный интеграл от функции f(x) в пределах от a до x, т.е. положим

С геометрической точки зрения этот интеграл равен площади криволинейной трапеции, лежащей под графиком функции y=f(x) на отрезке от a до x. Используя наглядные геометрические соображения, покажем, что введенная функция F(x) является одной из первообразных функции f(x), т.е. убедимся в том, что F'(x) = f(x). Пусть ∆x – некоторое приращение аргумента x. Очевидно, что разность F(x+∆x) - F(x) равна площади заштрихованной "узкой" криволинейной трапеции на рис.4. Площадь этой трапеции при малом ∆x мало отличается от площади f(x)∆x прямоугольника с основанием ∆x и высотой f(x). Отсюда ясно, что при малом ∆x отношение {F(x+∆x) - F(x)}/ ∆x мало отличается от высоты f(x) указанного выше прямоугольника. Так как предел при ∆x→0 данной дроби равен производной F'(x), то F'(x)=f(x). Итак, функция F(x) является одной из первообразных функции f(x). Следовательно, любая первообразная Ф(x) функции f(x) имеет вид

Уточним теперь с помощью этой формулы связь между определенным интегралом _a∫^bf(x)dx и любой первообразной Ф(x) функции f(x). Полагая в формуле последовательно x=a и x=b и учитывая очевидное из наглядных геометрических соображений равенство

получим

Поэтому

Данная формула является одной из основных формул интегрального исчисления и называется формулой Ньютона-Лейбница.

Рассмотрим основные теоремы интегрирования.

1.

2. Перестановка пределов интегрирования: если существует при a<b, то существует

3. Теорема о разбиении интеграла.

Если существуют интегралы и , то существует также и для любого взаимного расположения точек a, b, c: =+.

4. Если существует , то для любой постоянной α =.

5. Если существуют интегралы и , то существует также и =+.

6. Первая теорема о среднем значении. Если f(x) интегрируема на [a, b] и m≤f(x)≤M, то существует число μ, m≤μ≤M, такое, что В частности, если f(x) непрерывна на [a, b], то существует число ξ, a<ξ<b, такое, что

7. Вторая теорема о среднем значении. Если f(x) монотонна и ограничена, а g(x) интегрируема, то на [a, b] существует такая точка ξ, что=+.

Важным частным случаем определенного интеграла является несобственный интеграл, у которого один из пределов представляет собой бесконечность.