Выражение векторного произведения (вп) в декартовых прямоугольных координатах (дпк)

Теорема. Если два вектора определены своими ДПК

,

то их ВП имеет вид

(1)

Для запоминания этой формулы удобно использовать символ определителя (см. предыдущий пункт) и переписать ее в виде

.

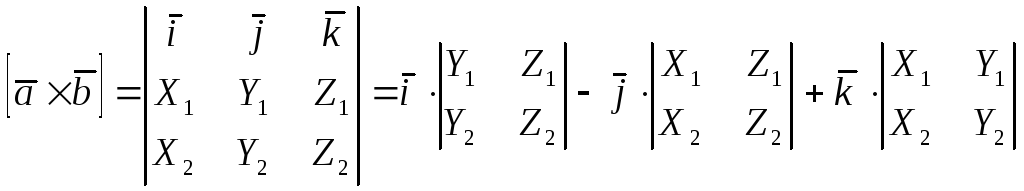Доказательство теоремы. Учитывая, что базисные векторы взаимно ортогональны, образуют правую тройку , имеем

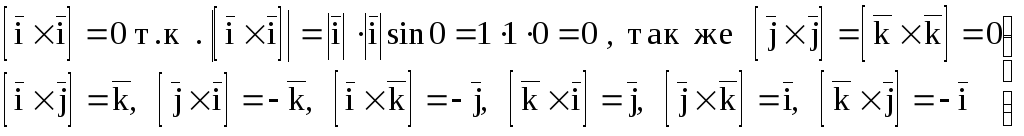(2)

Перемножая векторно , получим

Из этого равенства и соотношений (2) получаем разложение (1).

Следствие. Если два вектора и коллинеарны, то их координаты пропорциональны:

.

Доказательство. Из равенства нулю векторного произведения и из формулы 7 имеем

, ч.т.д.

4. Смешанное произведение трех векторов

Пусть даны три вектора . Если вектор векторно умножается на вектор , а затем полученный вектор скалярно умножается на вектор , то в результате получается число , называемое смешанным произведением векторов .

Из определения следует геометрический смысл смешанного произведения трех векторов:

Смешанное произведение равно объему параллелепипеда, построенного на приведенных к общему началу векторах , взятому со знаком плюс, если тройка правая, и со знаком минус, если тройка левая. Если же векторы компланарны, то.

Отсюда видно, что .

Поэтому можно записать смешанное произведение трех векторов просто в виде

,

не указывая, какие именно два вектора перемножаются векторно.

Следствие 1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Следствие 2.

Выражение смешанного произведения в декартовых координатах

Теорема. Если три вектора определены своими ДПК

,

то смешанное произведение равно определителю, строки которого соответственно равны координатам перемножаемых векторов:

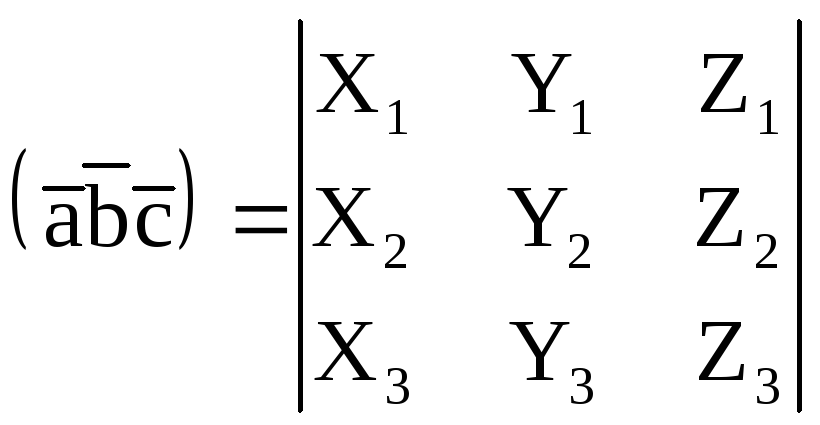
Доказательство. Так как

,

то скалярное произведение этих векторов равно

ч.т.д.

Следствие. Необходимым и достаточным условием компланарности трех векторов

является равенство нулю определителя, строками которого являются координаты этих векторов:

.

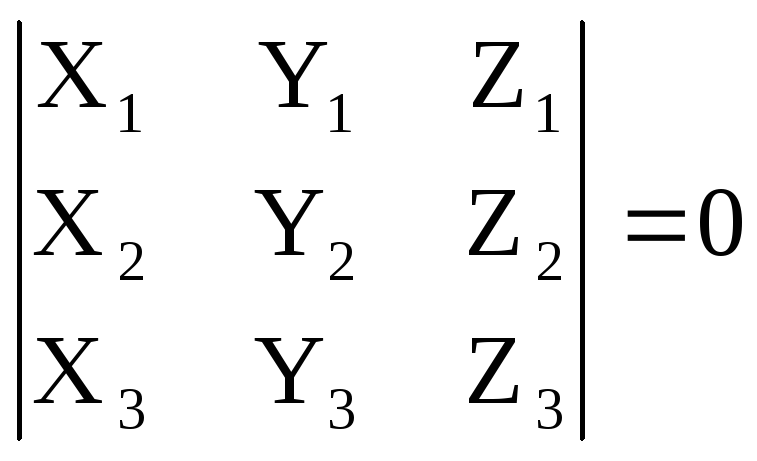5. Аналитическая геометрия на плоскости

1. Различные виды уравнений прямой на плоскости Общее уравнение прямой

Уравнение

Ax+By+C=0 (1)

с произвольными коэффициентами A, B и C такими, что A и B не равны одновременно нулю, называется общим уравнением прямой L.

Уравнение (1) имеет хотя бы одно решение , т.е. существует точка , координаты которой удовлетворяют уравнению (1):

. (2)

Вычитая из уравнения (1) тождество (2), получаем уравнение

, (3)

эквивалентное уравнению (1).

Если точка лежит на прямой L, то ее координаты удовлетворяют уравнению (3), векторы , перпендикулярный к прямой L и перпендикулярны и их скалярное произведение

равно нулю. Если же точка не лежит на прямой L, то ее координаты не удовлетворяют уравнению (3).

Итак, уравнение (3) определяет прямую L, проходящую через точку и перпендикулярную вектору . Этот вектор будем называть нормальным вектором прямой (1).

Уравнение прямой, проходящей через две заданных точки и :