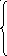- •Оглавление
- •Общие методические указания по изучению дисциплины
- •Основные теоретические положения математического анализа
- •Теория множеств
- •Основные свойства и графики элементарных функций
- •Предел функции, непрерывность функции, производная функции
- •Анализ функций одной и двух переменных
- •Интегрирование функций
- •Определенный интеграл, основные теоремы
- •Способы интегрирования
- •Дифференциальные уравнения
- •Понятие дифференциального уравнения
- •Дифференциальные уравнения первого порядка Общие сведения
- •Уравнение первого порядка с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Линейное уравнение первого порядка
- •Векторная алгебра
- •Понятие вектора и линейные операции над векторами Понятие вектора
- •Линейные операции над векторами
- •Свойства сложения векторов:
- •Понятие линейной зависимости векторов
- •Линейные комбинации двух векторов
- •Линейные комбинации трех векторов
- •Понятие базиса. Аффинные координаты
- •Проекция вектора на ось
- •Декартова прямоугольная система координат (дпск) в пространстве.
- •Полярная система координат
- •Скалярное произведение двух векторов Определение скалярного произведения (сп)
- •Геометрические свойства сп
- •Алгебраические свойства сп
- •Выражение скалярного произведения (сп) в декартовых прямоугольных координатах (дпк)
- •Векторное произведение двух векторов Правые и левые тройки векторов и системы координат
- •Векторное произведение двух векторов (вп)
- •Геометрические свойства вп
- •Алгебраические свойства векторного произведения (вп)
- •Понятие матрицы и определителя второго и третьего порядка
- •Выражение векторного произведения (вп) в декартовых прямоугольных координатах (дпк)
- •Смешанное произведение трех векторов
- •Выражение смешанного произведения в декартовых координатах
- •Аналитическая геометрия на плоскости
- •Различные виды уравнений прямой на плоскости Общее уравнение прямой
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой в отрезках
- •Каноническое уравнение прямой
- •Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
- •Кривые второго порядка
- •Эллипс Определение эллипса и вывод его канонического уравнения
- •Исследование формы эллипса
- •Эксцентриситет эллипса
- •Гипербола Определение гиперболы и вывод ее канонического уравнения
- •Исследование формы гиперболы
- •Асимптоты гиперболы
- •Равнобочная гипербола
- •Сопряженная гипербола
- •Эксцентриситет и фокальные радиусы гиперболы
- •Парабола Определение параболы и ее уравнение
- •Исследование формы параболы
- •Общее свойство кривых второго порядка - эллипса, гиперболы и параболы Директриса эллипса, гиперболы и параболы
- •Аналитическая геометрия в пространстве Плоскость как поверхность первого порядка
- •Неполные уравнения плоскости
- •Уравнение плоскости в отрезках
- •Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •Уравнение прямой в пространстве
- •Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой
- •Некоторые дополнительные предложения и примеры
- •Линейная алгебра
- •Матрицы. Основные определения
- •Действия над матрицами
- •Обратная матрица
- •Системы линейных уравнений Система линейных уравнений
- •Методы решения системы n линейных уравнений с n неизвестными
- •Методы решения системы m линейных уравнений с n неизвестными. Метод Гаусса
- •Система m линейных уравнений с n переменными
- •Задачи оптимизации
- •Математические модели оптимизации
- •Задачи линейного программирования
- •Задачи динамического программирования
- •Примеры решения типовых задач Задачи по математическому анализу, линейной алгебре и методам оптимизации
- •Варианты заданий к контрольным работам
- •Контрольная работа №1
- •Задача 6. Аналитическая геометрия на плоскости а) Линии первого порядка
- •Контрольная работа №2
- •Задачи для самостоятельной работы Пределы и непрерывность
- •Производная и ее применение
- •Определенный интеграл
- •Несобственные интегралы
- •1. Дифференциальные уравнения первого порядка
- •2. Однородные дифференциальные уравнения первого порядка
- •Вопросы к зачету
- •Определенный интеграл, основные теоремы.
- •Вопросы к экзамену
- •Определенный интеграл, основные теоремы.
- •Системы линейных уравнений.
- •Задачи линейного программирования.
- •Литература
- •К.Т.Н., доц. Тугуз Юрий Рамазанович Математика
- •Учебно-методическое пособие
- •344002, Г. Ростов-на-Дону, ул. Пушкинская, 70
-
Обратная матрица
Пусть
задана квадратная матрица
![]() порядка n.
порядка n.
Определение. Квадратная матрица А-1 порядка n называется обратной к матрице А, если она удовлетворяет соотношению
-
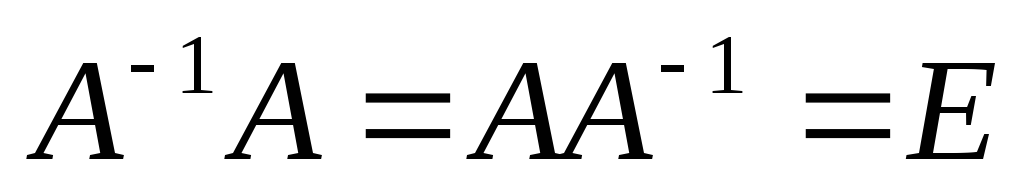 .
.(1)
Присоединенной
матрицей квадратной матрицы А называется
матрица А*, каждый элемент
![]() которой есть алгебраическое дополнение
элемента
которой есть алгебраическое дополнение
элемента
![]() транспонированной матрицы А, т.е.
транспонированной матрицы А, т.е.
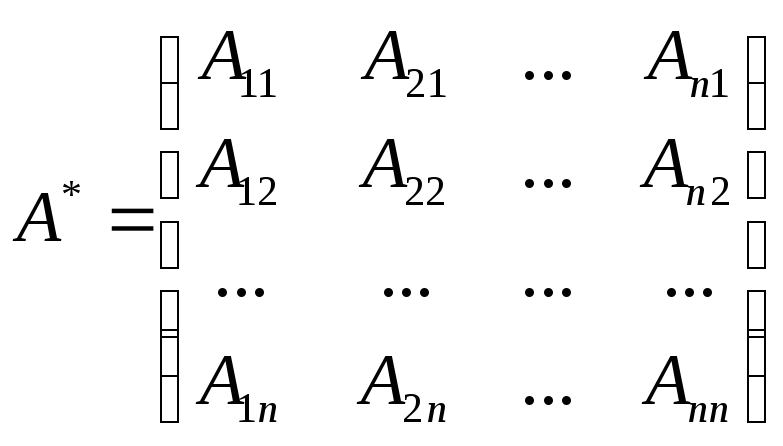 .
.
Квадратная матрица А называется невырожденной (неособенной), если ее определитель |A| отличен от нуля, и вырожденной, если |A|=0.
Теорема. Для всякой невырожденной матрицы А существует единственная обратная матрица А-1, определяемая следующим выражением:
|
|
(2) |
Обратная матрица обладает следующими основными свойствами:
-
Определитель обратной матрицы равен обратной величине определителя исходной матрицы, т.е. |A-1|=
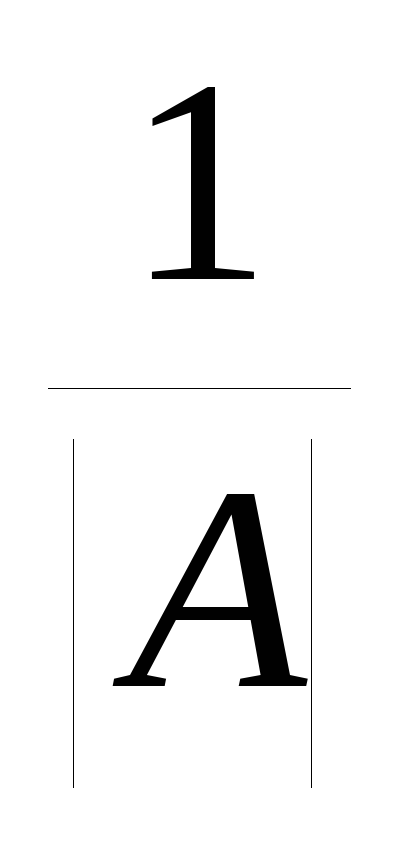 .
. -
Произведение двух невырожденных матриц А и В является невырожденной матрицей и
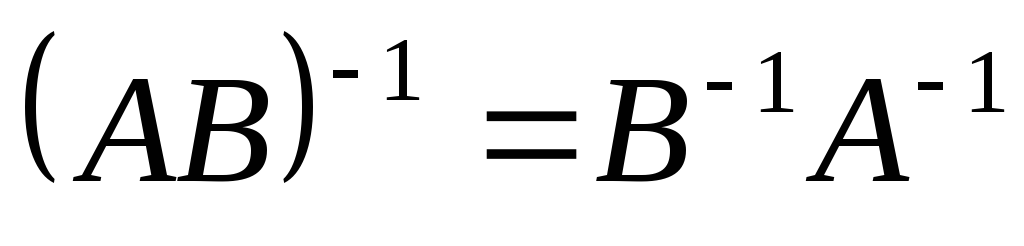 .
. -
Если матрица А невырожденная, то
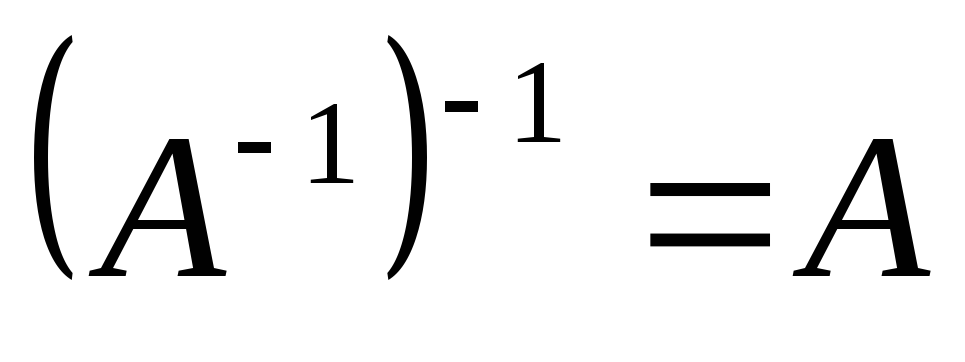 .
. -
Обратная матрица к транспонированной является транспонированной матрицей к обратной, т.е.
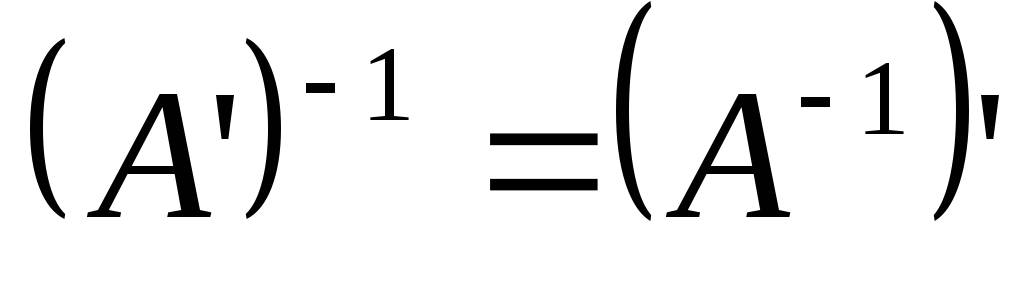 .
.
-
Системы линейных уравнений Система линейных уравнений
Системой m линейных уравнений с n неизвестными называется система m алгебраических уравнений первой степени вида
|
|
(1) |
где
![]() – неизвестные, подлежащие определению;
– неизвестные, подлежащие определению;
![]() – числа,
называемые коэффициентами при неизвестных;
– числа,
называемые коэффициентами при неизвестных;
![]() – числа,
называемые свободными членами.
– числа,
называемые свободными членами.
Решением
системы уравнений (1) называется
совокупность n
чисел
![]() таких, что если в каждое уравнение
системы вместо
неизвестных подставить эти числа (
таких, что если в каждое уравнение
системы вместо
неизвестных подставить эти числа (![]() вместо
вместо
![]() ,
,
![]() вместо
вместо
![]() вместо
вместо
![]() ),
то все уравнения обратятся в тождества.
),
то все уравнения обратятся в тождества.
Если система линейных уравнений (1) имеет хотя бы одно решение, то она называется совместной. В противном случае система называется несовместной.
Совместная система, имеющая единственное решение, называется определенной, а система, имеющая более одного решения – неопределенной.
Две системы линейных уравнений называются эквивалентными, если любое решение каждой из них является одновременно решением и другой системы.
Две произвольные несовместные системы считаются эквивалентными.
Системе
линейных уравнений (1) поставим в
соответствие матрицу
![]() и расширенную матрицу
и расширенную матрицу
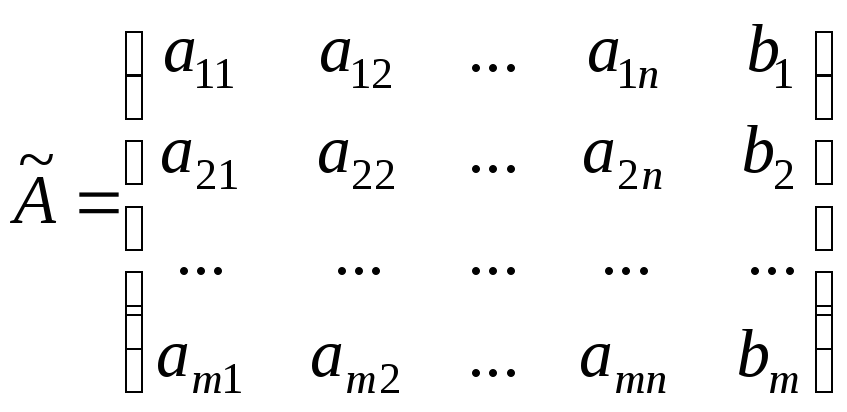 ,
,
полученную присоединением к матрице А столбца свободных членов.
Методы решения системы n линейных уравнений с n неизвестными
Рассмотрим систему n линейных уравнений с n неизвестными
|
|
(2) |
Определитель |A| матрицы А называется определителем системы (1).
Теорема Крамера. Если определитель |A| системы (1) отличен от нуля, то система совместна и имеет единственное решение.
|
|
(3) |
Из формулы (2) следует, что если система (1) совместна, то она обладает единственным решением.
Формулы (2) называются формулами Крамера.
Непосредственной
подстановкой значений
![]() ,
во все уравнения системы убедимся в
том, что они образуют ее решение:
,
во все уравнения системы убедимся в
том, что они образуют ее решение:
 .
.
При
![]() ,
,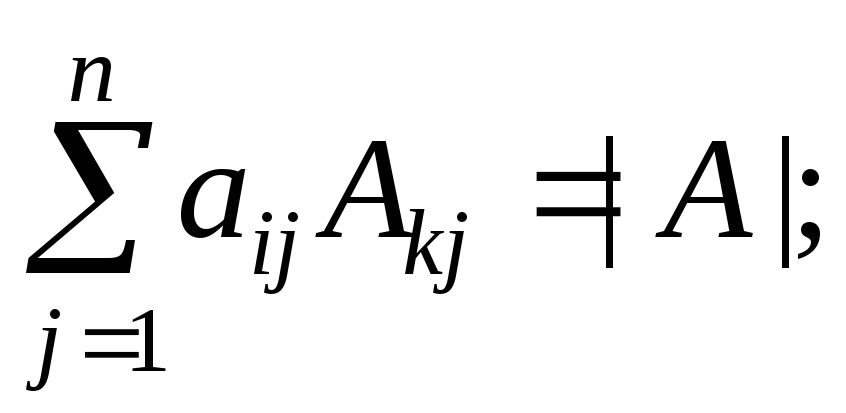 при
при
![]() ,
,
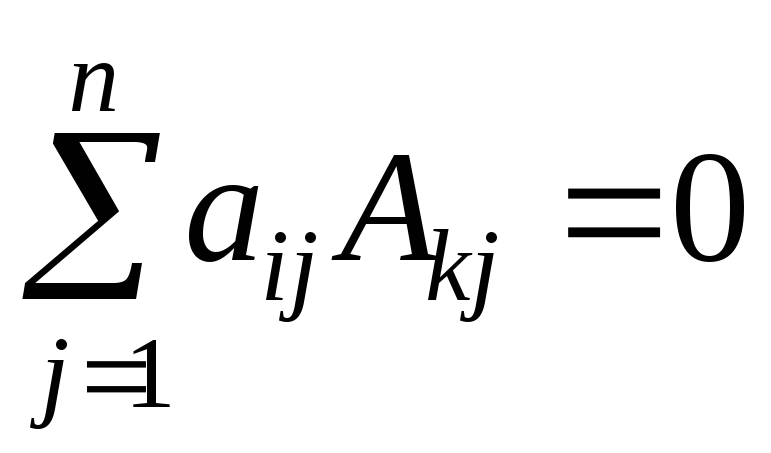 .
.
Таким образом, получим
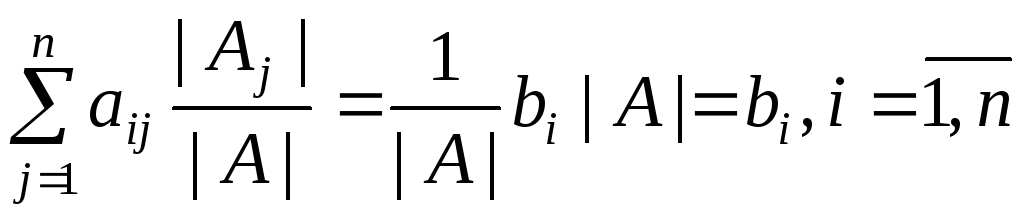 .
.
Пример. Решить систему линейных уравнений методом Крамера:
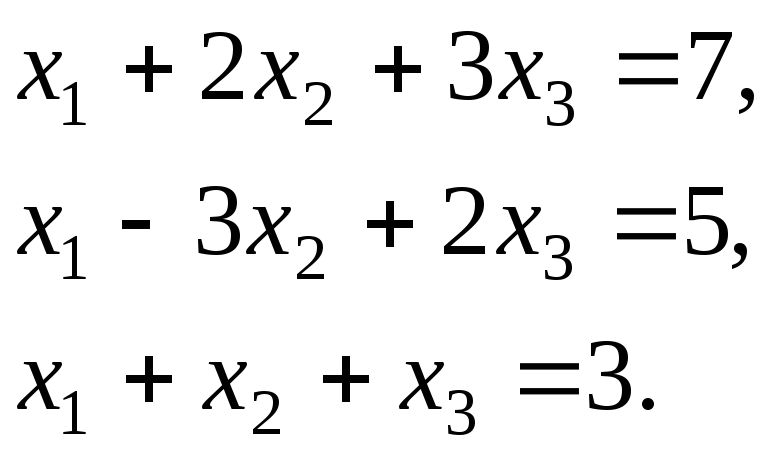
Решение.
Вычислим определитель
![]() :
:
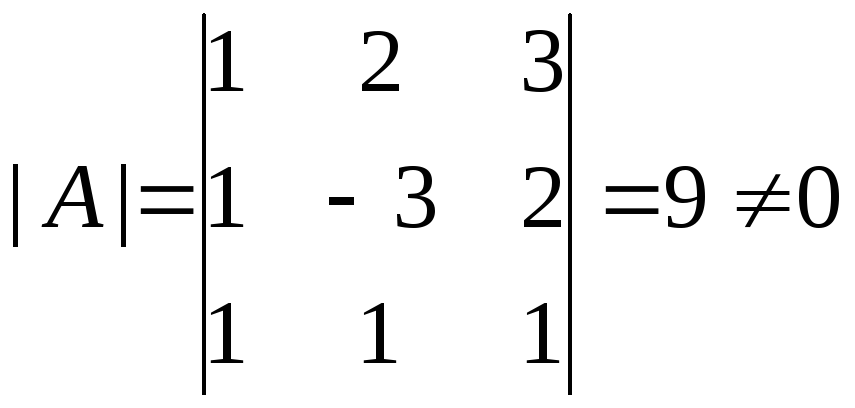
 ,
,
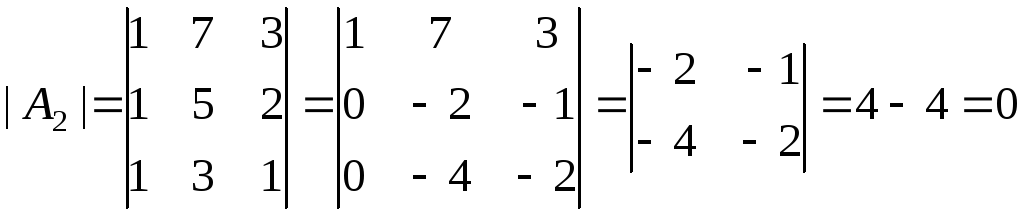 ,
,
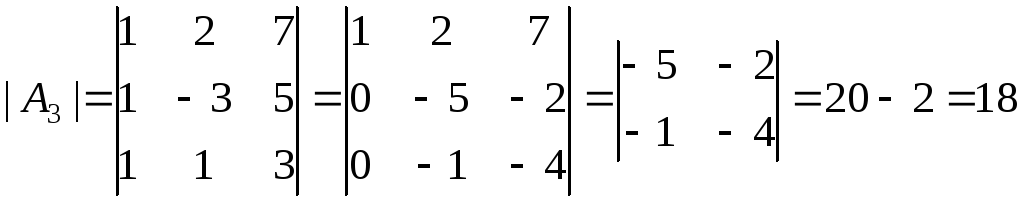 ,
,
откуда
![]()
Решение системы линейных уравнений с определителем |A|, отличным от нуля, можно найти с помощью обратной матрицы. Для этого запишем систему (1) в виде матричного уравнения
|
АХ=В, |
(4) |
где
![]() .
.
Решение матричного уравнения (4) имеет вид
|
|
(5) |
Пример. Решить систему линейных уравнений с помощью обратной матрицы
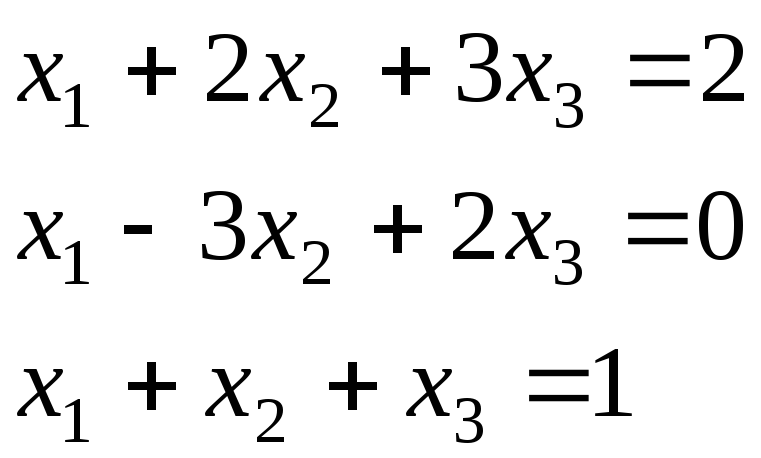
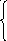
Решение. Вычислим для матрицы
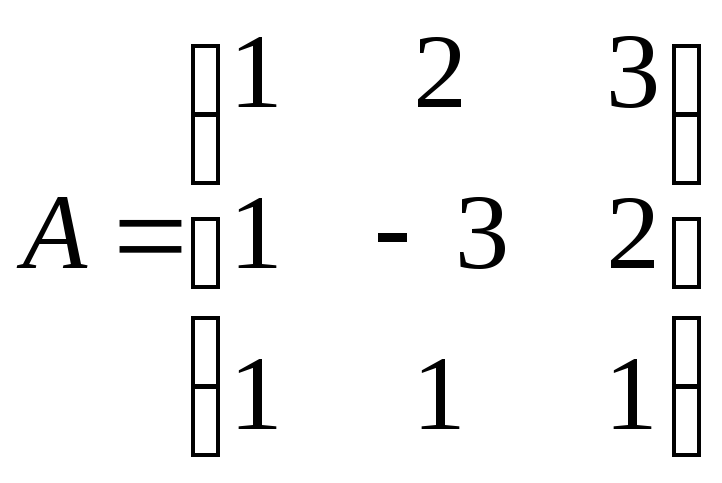
ее обратную матрицу
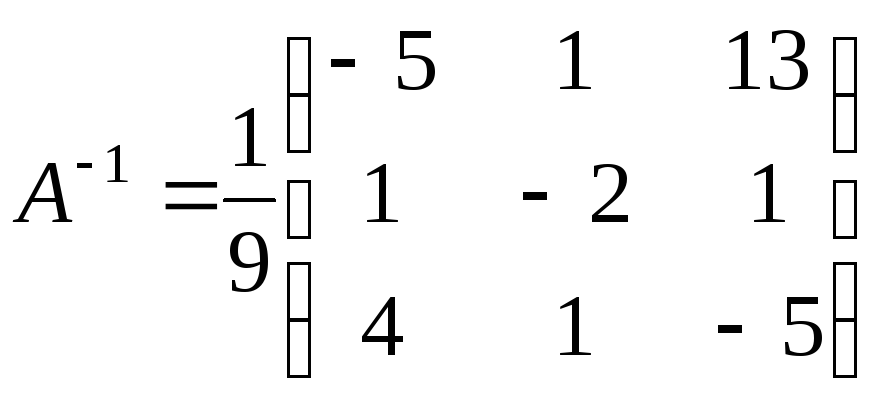 .
.
Определим неизвестную матрицу-столбец Х:
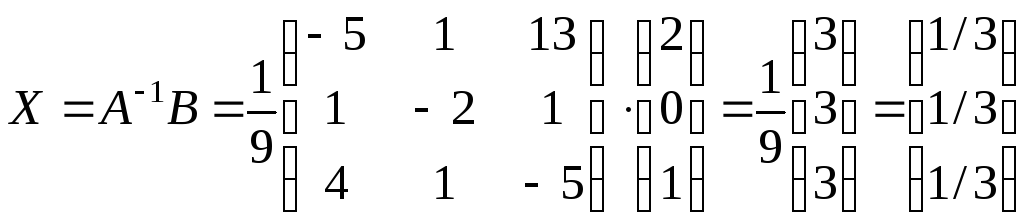 ,
,
откуда
![]()
Формулы
Крамера (3) могут быть получены из
выражения (5). Действительно, запишем
матричное равенство
![]() в развернутом виде:
в развернутом виде:
 .
.
Из полученного выражения непосредственно следуют формулы Крамера:
![]() .
.