Исследование формы гиперболы

Займемся исследованием гиперболы, определяемой уравнением

.

Прежде всего заметим, что в уравнение гиперболы обе координаты входят только в четных степенях. Следовательно, если некоторая точка М₀(х₀;у₀) лежит на гиперболе, то на гиперболе будут лежать также точки М₁(х₀;-у₀); М₂(-х₀;у₀); М₃(-х₀;-у₀). Отсюда следует, что гипербола является кривой, симметричной относительно обеих координатных осей и начала координат. Это позволяет изучение формы гиперболы ограничить первым квадрантом, а затем получившуюся кривую с помощью зеркального отображения построить во всех четырех квадрантах.

В случае канонического задания гиперболы координатные оси являются осями симметрии гиперболы. Таким образом, гипербола, как и эллипс, - центральная кривая.

От начала координат на оси абсцисс вправо и влево отложим отрезок, длина которого равна а, и построим точки A₁(a;0) и А₂(-а;0), а на оси ординат вверх и вниз отложим отрезок длиной b и построим точки В₁(0;b) и B₂(0;-b). Затем через точки А₁, А₂, В₁, В₂ проведем прямые, параллельные координатным осям, до их взаимного пересечения и таким образом построим прямоугольник (рис. 6), который назовем основным прямоугольником гиперболы.

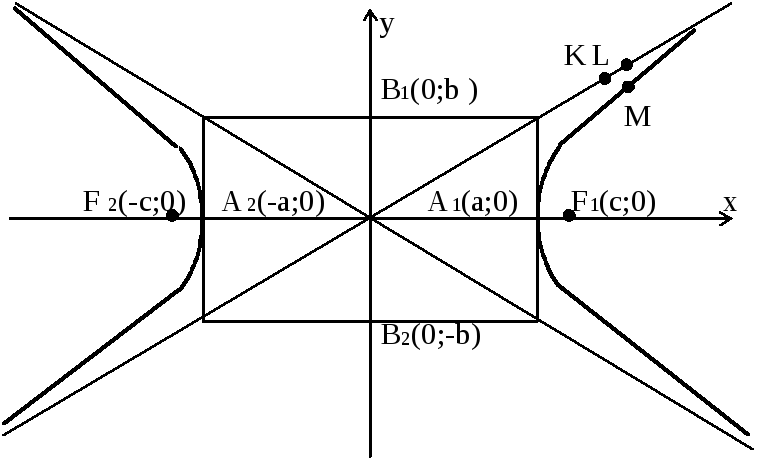
Рис. 4

Раствором циркуля, равным расстоянию А₁В₁, из начала координат как из центра, сделаем засечки на оси абсцисс. При этом мы найдем точки F₁ и F₂. Действительно, из прямоугольного треугольника ОА₁В₁: ОА₁=а, ОВ₁=b. Следовательно, на основании равенства

a² + b² = c², т.е. В₁А₁=с.

Определим теперь у из канонического уравнения гиперболы :

(9)

Так как исследование гиперболы будет вестись в первом квадранте, то в этом равенстве надо перед корнем взять знак плюс:

(10)

и рассматривать х  0.

1. Если 0  х<a, то у получает мнимые значения. Следовательно, точек гиперболы с абсциссами х, 0  х<a не существует.

2. Если х=а, то у=0. Следовательно, точка А₁(а;0) принадлежит гиперболе.

3. Если х>а, то у>0, причем при возрастании х возрастает и у.

Когда х неограниченно возрастает, у также неограниченно возрастает. Следовательно, при неограниченном возрастании х ветвь гиперболы уходит в бесконечность.

Отсюда следует, что гипербола представляет собой кривую, состоящую из двух бесконечных ветвей (для правой ветви r₁ - r₂ = -2a, для левой r₁ - r₂ = + 2a) с двумя взаимно перпендикулярными осями симметрии, причем ни одной точки гиперболы не находится внутри основного прямоугольника.

Отрезок А₂А₁ и его длина 2а называются действительной осью гиперболы, отрезок ОА₁ и его длина а называются действительной полуосью гиперболы. Отрезок В₂В₁ и его длина 2b называются мнимой осью гиперболы; отрезок ОВ₁ и его длина b называются мнимой полуосью гиперболы. Длина 2с отрезка F₂F₁ называется фокусным расстоянием. Точки пересечения гиперболы с действительной осью А₁ и А₂ называются вершинами гиперболы.

Асимптоты гиперболы

Пусть Г – какая-нибудь линия, М – переменная точка на ней, A – некоторая прямая. Если возможно такое движение точки М по линии Г, что:

1. точка М уходит в бесконечность;

2. при этом расстояние от точки М до прямой A стремится к нулю, – то говорят, что линия Г асимптотически приближается к прямой A. Прямая A в таком случае называется асимптотой линии Г.

Асимптотами гиперболы называются прямые, имеющие уравнения:

и (11)

Эти прямые являются диагоналями основного прямоугольника. Построим гиперболу и рассмотрим какую-нибудь точку М(х;у), лежащую на гиперболе в первом квадранте.

Выясним, как в первом квадранте по мере возрастания х будет изменяться расстояние от точки М гиперболы до асимптоты . Обозначим через N точку асимптоты с абсциссой х: N(x;Y), где Y=. Тогда

(12)

Так как а  х, то в скобках первое слагаемое всегда больше второго, следовательно, Y-y>0, а это означает, что при одной и той же абсциссе точка гиперболы лежит под соответствующей точкой асимптоты.

Преобразуя неравенство (12):

, (13)

убеждаемся, что длина отрезка MN по мере возрастания х уменьшается, и когда х неограниченно растет, то MN стремится к нулю. Так как MN больше расстояния МК от точки M до асимптоты, то при этом МК и подавно стремится к нулю.

Аналогичное рассуждение можно провести в любом квадранте.

Итак, прямые в смысле определения являются асимптотами гиперболы

.

При построении гиперболы обычно строят основной прямоугольник и проводят асимптоты, так как они позволяют точнее вычерчивать гиперболу.