Глава 10. Картографические проекции используемые в навигации
10.1. Классификация картографических проекций
Для получения плоского изображения земной поверхности нужно сначала нанести на плоскость систему координатных линий, которая соответствовала бы таким же линиям на сфере.
Имея нанесенную на плоскость систему меридианов и параллелей, можно теперь нанести на эту сетку любые точки Земли.
Картографическая сетка– условное изображение географической сетки земных меридианов и параллелей на карте в виде прямых или кривых линий.
Картографическая проекция– способ построения картографической сетки на плоскости и изображение на ней сферической поверхности Земли, подчиненный определенному математическому закону.
Картографические проекции по характеру искаженийделятся на:
Равноугольные (конформные)– проекции, не искажающие углов. Сохраняется подобие фигур. Масштаб изменяется с изменением широты (j) и долготы (l). Отношение площадей не сохраняется на карте. (о. Гренландия»Африке; на самом делеS Африки≈ 30,1 млн. км2аSГренландии ≈ 2,1 млн. км2, то есть в 13,8 раза больше.
Равновеликие (эквивалентные)– проекции, на которых масштаб везде одинаков и площади на картах пропорциональны соответствующим площадям на Земле. Равенства углов и подобия фигур не сохраняются. Масштаб длин в каждой точке не сохраняется по разным направлениям.
Произвольные– проекции, заданные несколькими условиями, но не обладающие ни свойствами равноугольности, ни свойствами равновеликости.
Картографические проекции по способу построениякартографической сетки делятся на:
Цилиндрические – проекции, на которых картографическая сетка меридианов и параллелей получается путем проецирования земных координатных линий на поверхность цилиндра, касающегося условного глобуса (или секущего его), с последующей разверткой этого цилиндра на плоскость.
Прямая цилиндрическая проекция®ось цилиндра совпадает с осью Земли;
Поперечная цилиндрическая проекция®ось цилиндра перпендикулярна оси Земли;
Косая цилиндрическая проекция®ось цилиндра наклонена к оси Земли под углом, отличным от 0°и 90°.
Конические – проекции, на которых проецирование выполняется не на цилиндр, а на конус. По аналогии с цилиндрическими, конические также могут быть прямыми, поперечными или косыми.
Азимутальные– проекции, в которых меридианы – радиальные прямые, исходящие из одной точки под углами, равными, соответствующим углам в натуре, а параллели – концентрические окружности, проведенные из точки схождения меридианов (ортографические, внешние, стереографические, центральные, полярные, экваториальные, горизонтные).
Из всего многообразия картографических проекций, более подробно рассмотреныте из них, которые в той или иной степени применяются в судовождении.
10.2. Поперечная цилиндрическая проекция
Поперечная цилиндрическая проекция применяется для составления морских навигационных карт и карт-сеток на приполюсные районы для j Г>75¸80°N(S).
Как и нормальная цилиндрическая проекция Меркатора (см. п. 6.2), эта проекция является равноугольной (не искажает углы).
При построении и использовании карт в данной проекции применяется система квазигеографическихкоординат(«квази» (лат.) – как бы»), которая получается следующим образом (рис. 10.1):
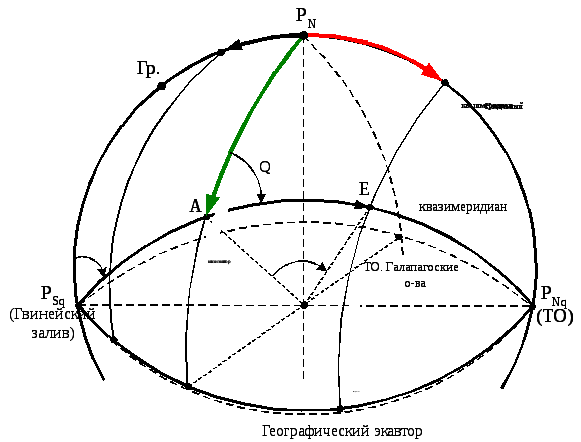
Рис. 10.1. Поперечная цилиндрическая проекция
Северный полюс условно помещается в точку с координатами: jГ= 0°,lГ= 180°(р-н Тихого океана), а южный полюс – в точку с координатами:jГ= 0°,lГ= 0°(р-н Гвинейского залива).
Полученные точки называются квазиполюсами:PNq– северным,PSq– южным.
Проведя квазимеридианы и квазипараллели относительно квазиполюсов, получим новую систему координат, повернутую на 90°относительно географической.
Координатными осями этой системы будут:
®начальный квазимеридиан– большой круг, проходящий через северный географический полюс (PN) и квазиполюсы (PNqи PSq), он совпадает с географическим (lГ= 0°иlГ= 180°) Гринвичским (начальным) меридианом;
®квазиэкватор– большой круг, проходящий через географический полюс (PN) и точки на экваторе с долготами:lГ= 90°Е(р-н Индийского океана) иlГ= 90°W(р-н Галапагоских островов).
Координатными линиями этой системы являются:
®квазимеридианы– большие круги, проходящие через квазиполюсы;
®квазипараллели– малые круги, плоскости которых параллельны плоскости квазиэкватора.
Положение любой точки на поверхности Земли на картах в поперечной цилиндрической проекции определяется квазиширотой (jq)иквазидолготой(lq).
Квазиширота (jq) ®угол при центре Земли (шара) между плоскостью квазиэкватора и радиусом, проведенным в данную точку земной поверхности. Квазиширота определяет положение квазипараллелей; отсчитывается от квазиэкватора к квазиполюсам: кPNq®+jqи кPSq ®–jqот 0°до 90°.
Квазидолгота (lq) ® двугранный угол при квазиполюсе между плоскостями начального квазимеридиана и квазимеридиана данной точки. Квазидолгота определяет положение квазимеридианов; отсчитывается от географического полюсаРNпо квазиэкватору к востоку (+lq) и к западу (–lq) от 0°до 180°.
Началом отсчета квазигеографических координат является географический северный полюс (т. РN).
Основные уравнения поперечной цилиндрической равноугольной проекции имеют вид:
(10.1)
где
(10.2)
– радиус Земли (м);
mиn– частные масштабы по квазимеридиану и квазипараллели.
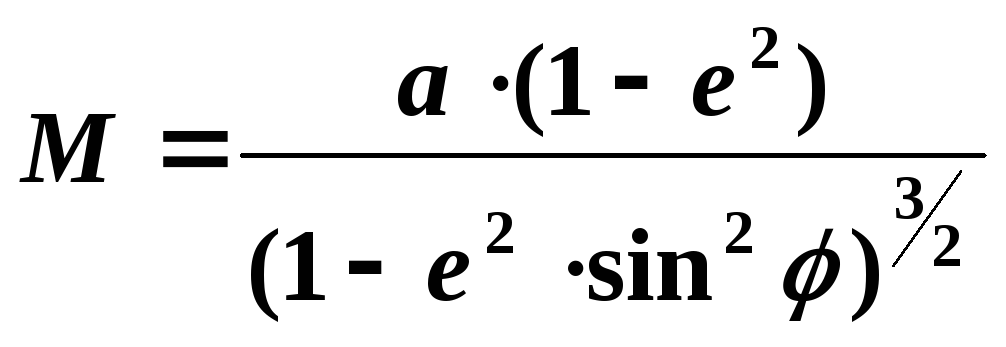(10.3)
(10.4)
где а = 3437,74¢.
Для эллипсоида Красовского: а = 6378245 м.
Переход от географических координат к квазикоординатам выполняется по формулам:
(10.5)
(10.6)
Прямой линией на такой карте изображается квазилоксодромия, пересекающая квазимеридианы под одним и тем же квазикурсомКq(рис. 10.2).
Рис. 10.2. Квазилоксодромия
Локсодромия,вследствие кривизны географических меридианов, сходящихся на полюсе, будет изображаться кривой линией, обращенной выпуклостью к экватору.
Ортодромияже представит собой кривую малой кривизны, обращенную выпуклостью в сторону ближайшего квазиполюса.
Таким образом, при построении квазигеографической сетки карты используются формулы, аналогичные формулам для нормальной проекции Меркатора с заменой в них географических координат квазигеографическими.
Главный масштаб карт и карт-сеток относят к квазиэкватору.
Географические меридианы изображаются кривыми, близкими к прямым линиям.
Географические параллели изображаются кривыми линиями, близкими к окружностям.
Квазикурс (Кq)– угол между квазисеверной частью квазимеридиана и направлением носовой части продольной оси судна (отсчитывается по часовой стрелке от 0°до 360°).
Для перехода от географических направлений к направлениям в квазигеографической системе координат используется угол перехода Q– угол между географическим меридианом и квазимеридианом, значение которого можно получить из треугольникаАPNPNq(рис. 10.1).
(10.7)
(10.8)
В широтах >80°, когдасоs jq»1, получим:
(10.9)
т.е. в высоких широтах угол перехода практически равен долготе точки (Q »1).
Прокладка курса на такой карте относительно географических или квазигеографических меридианов осуществляется по формуле:
(10.10)
Для прокладки расстояний необходимо пользоваться специальными вертикальными шкалами с линейным масштабом в морских милях, находящимися за боковыми рамками карт.
Для приполюсных районов Северного Ледовитого океана (СЛО) издаются карты М 1:500.000, на которых красным цветомнанесены квазипараллели, ачерным цветом– географические меридианы и параллели с двойной оцифровкой красным и зеленым цветом. Это позволяет использовать карту-сетку в двух районах, симметричных относительно географических меридианов 0°…..180°и 90°Е…..90°W.
По аналогии с нормальной проекцией Меркатора на картах и картах-сетках в поперечной проекции Меркатора прямой линией изображается квазилоксодромия– кривая на поверхности Земли, пересекающая квазимеридианы под постоянным угломКq(приjq£15°ее можно принимать за кратчайшую линию).
Уравнение квазилоксодромии:
(10.11)
где lq2 – lq1– разность квазидолгот точек;
Dq2 – Dq1– разность квазимеридиональных частей (табл. 26 «МТ-75» или табл. 2.28а«МТ-2000»).
Уравнение (10.11) используется при аналитическом счислении в квазигеографической системе координат.
Если известен главный масштаб карты или карты-сетки
(10.12)
по квазиэкватору, то частный масштаб
(10.13)
в точке с квазиширотой jqвычисляется по формуле:
(10.14)
или
(10.15)
(масштаб карт увеличивается по мере удаления от квазиэкватора).