6.2.2. Меркаторская проекция
Предложенная Меркатором проекция относится к разряду нормальных цилиндрических равноугольных проекций.
Карты, построенные в этой проекции, называются меркаторскими, а проекция ®проекция Меркатораилимеркаторская проекция.
В меркаторской проекции все меридианы и параллели прямые и взаимноперпендикулярные линии, а линейная величина каждого градуса широты постепенно увеличивается с возрастанием широты, соответственно растягиванию параллелей, которые все в этой проекции по длине равны экватору.
Проекция Меркатора по характеру искажений относится к классу равноугольных.
Для получения морской навигационной карты в проекции Меркатора условный глобус помещают внутрь касательного цилиндра таким образом, чтобы их оси совпали.
Затем проецируют из центра глобуса меридианы на внутренние стенки цилиндра. При этом все меридианы изобразятся прямыми, параллельными между собой и перпендикулярными экватору линиями. Расстояния между ними равны расстояниям между теми же меридианами по экватору глобуса. Все параллели растянутся до величины экватора. При этом параллели, ближайшие к экватору, растянутся на меньшую величину и по мере удаления от экватора и приближения к полюсу величина их растяжения увеличивается.
Закон растяжения параллелей (рис. 6.1).
|
а) |
б) |
в) |
Рис. 6.1. Закон растяжения параллелей
Rиr– радиус Земли и произвольной параллели (СС¢).
j– широта произвольной параллели (СС¢).
Из прямоугольного треугольника ОС¢Кполучим:
(6.4)
Обе части равенства умножим на 2p, получим:
(6.5)
где 2p×R– длина экватора;
2p×r – длина параллели в широтеj.
Следовательно, длина экватора равна длине соответствующей параллели, умноженной на секанс широты этой параллели. Все параллели, удлиняясь до длины экватора, растягиваются пропорционально sec j.
Разрезав цилиндр по одной из образующих, и развернув его на плоскость, получим сетку взаимно перпендикулярных меридианов и параллелей (рис. 6.1б).
Эта сетка не удовлетворяет требованию равноугольности, т.к. изменились расстояния между меридианами по параллели, ибо каждая параллель растянулась и стала равной длине экватора. В результате фигуры с поверхности Земли перенесутся на сетку в искаженном виде. Углы в природе не будут соответствовать углам на сетке.
Очевидно, для того, чтобы не было искажений, т.е.чтобы сохранить на карте подобие фигур, а следовательно, и равенство углов, необходимо все меридианы в каждой точке растянуть настолько, на сколько растянулись в данной точке параллели, т.е. пропорциональноsec j.При этом эллипс на проекции вытянется в направлении малой полуоси и станет кругом, подобным острову круглой формы на поверхности Земли. Радиус круга станет равным большой полуоси эллипса, т.е. будет вsec j раз больше круга на поверхности Земли (рис. 6.1в).
Полученная таким образом картографическая сетка и проекция будут полностью удовлетворять требованиям, предъявленным к морским навигационным картам, т.е. проекцией Меркатора.
6.3. Уравнение проекции Меркатора
Покажем, что прямая линия на карте в меркаторской проекции действительно представляет собой локсодромию.
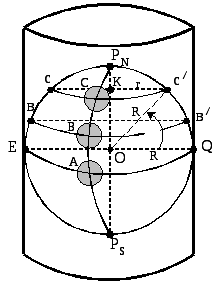
Локсодромия®кривая, пересекающая все меридианы под одним и тем же угломК(рис. 6.2).
Рис. 6.2. Локсодромия на земном шаре
Судно, совершающее плавание постоянным курсом, перемещается именно по локсодромии.
Уравнение локсодромии на поверхности эллипсоида имеет вид:
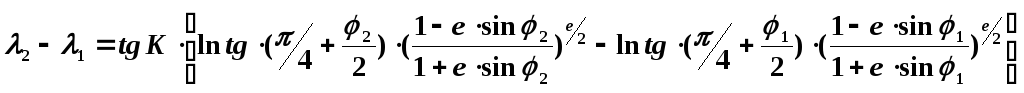(6.6)
Если пренебречь сжатием эллипсоида и приняв Землю за шар, то уравнение локсодромии примет вид:
(6.7)
Из формулы (6.7) выводятся следующиесвойства локсодромии:
– при К = 0°(180°) ® локсодромия совпадает с меридианом;
– при К = 90°(270°) ® локсодромия совпадает с параллелью, а при j = 0° – с экватором;
– при любых других К – локсодромия является логарифмической спиралью, стремящейся к полюсу, но никогда его не достигающей;
– локсодромия своей выпуклостью обращена к экватору.
Длину и направление локсодромии по известным координатам точек вычисляют по формулам аналитического счисления.
Напишем уравнение прямой, проходящей через т. А(Х0,У0) наклонно к осиХпод угломКравным курсу (рис. 6.3).
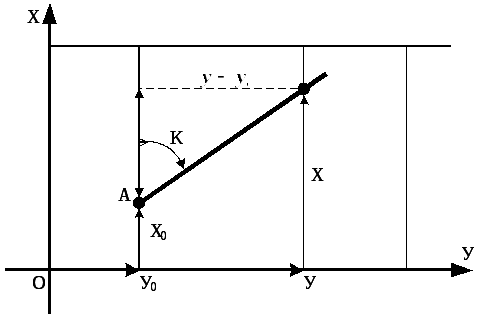
Рис. 6.3. Уравнение прямой
(6.8)
Подставим в полученное уравнение (6.5) вместо ХиУих выражения черезjиl, принимая для простоты Землю за шар:
(6.9)
где а – коэффициент пропорциональности определяющий расстояния между меридианами.
(6.10)
Тогда:
(6.11)
Это уравнение показывает, что прямая линия на меркаторской проекции действительно представляет собой локсодромию.
Таким образом, проводя на меркаторской проекции параллели в расстоянии МЧот экватора, удовлетворяются оба требования, предъявляемые к морской навигационной карте.