
- •Математика в 4-му класі початкової школи
- •Методика вивчення нумерації і арифметичних дій в 4-му класі.
- •Методика роботи над задачами в 4-му класі
- •Зміст курсу математика 4-го класу
- •Узагальнення та систематизація знань за третій клас. Нумерація трицифрових чисел
- •Арифметичні дії додавання і віднімання, множення і ділення
- •Узагальнення обчислювальних прийомів додавання і віднімання в межах 1000.
- •Додавання і віднімання по частинах
- •Пам'ятка Порозрядне додавання
- •Пам'ятка Порозрядне віднімання
- •Порозрядне додавання кількох чисел.
- •Пам'ятка Додавання (віднімання) способом округлення
- •1.Прийом укрупнення розрядних одиниць.
- •Узагальнення обчислювальних прийомів поза табличного множення і ділення
- •Прийом укрупнення
- •Прийом на підставі множення ( ділення) добутку на число
- •Прийом на підставі ділення числа на добуток
- •Прийом на підставі конкретного змісту дії ділення
- •Прийом на підставі множення (ділення ) суми на число
- •Правило множення на 9, 99, 999
- •Правило множення у випадках, якщо один з множників близький до розрядного двоцифрового або трицифрового числа
- •Узагальнення знань учнів про складені задачі.
- •Задачі на знаходження четвертого пропорційного.
- •Ускладнені задачі на знаходження четвертого пропорційного.
- •Задачі на спільну роботу.
- •Методика вивчення нумерації і арифметичних дій в 4-му класі. Усна та письмова нумерація багатоцифрових чисел .
- •Читання багатоцифрових чисел
- •Запис багатоцифрових чисел
- •Запис багатоцифрових чисел.
- •Читання багатоцифрових чисел
- •Методика вивчення додавання і віднімання багатоцифрових чисел
- •Письмове додавання і віднімання
- •Методика вивчення письмового множення і ділення багатоцифрових чисел.
- •Методика вивчення множення багатоцифрових чисел на одноцифрове число
- •Письмове множення на одноцифрове число.
- •Множення багатоцифрового числа, що закінчується нулями на одноцифрове
- •Методика вивчення ділення на одноцифрове число
- •Дидактична задача: формувати навички письмового ділення трицифрового
- •Дидактична задача: формувати навички письмового ділення трицифрового
- •Письмове ділення
- •Усне множення і ділення на розрядну одиницю.
- •Множення і ділення на розрядну одиницю: 10, 100, 1000...
- •Методика вивчення множення багатоцифрових чисел на двоцифрове число
- •Множення на числа, що закінчуються нулями
- •Множення чисел, що закінчуються нулями
- •Письмове множення на двоцифрове число
- •Методика вивчення ділення багатоцифрових чисел на двоцифрове число
- •Спосіб перевірки пробних цифр частки
- •Методика вивчення дробів
- •З двох дробів з рівними знаменниками
- •Чим на більше число рівних частин поділене ціле, тим менше величина кожної частини.
- •Якщо у дробів однакові чисельники та різні знаменники, то більший той дріб, в якого знаменник менший.
- •У дробів однакові чисельники та різні знаменники, то менший той дріб, в якого знаменник більший.
- •З двох дробів з однаковими чисельниками той, у якого знаменник .
- •Якщо чисельник і знаменник дробу помножити на одне й те саме натуральне число, то отри маємо дріб, який рівний даному.
- •Якщо чисельник і знаменник дробу розділити на одне й те саме натуральне число, то отри маємо дріб, який рівний даному.
- •Якщо чисельник і знаменник дробу помножити або розділити на одне й те саме натуральне число, то отри маємо дріб, який рівний даному.
- •Якщо в задачі треба знайти дріб від числа , треба: першою дією дізнатися про величину однієї частини, а другою дією знайти величину дробу.
- •Щоб знайти дріб від числа, треба число поділити спочатку на знаменник, і отриману частку помножити на чисельник.
- •Задачі з дробами
- •1. Знаходження частини від числа.
- •Методика роботи над задачами в 4-му класі Види простих задач 4-го класу та методика роботи над ними
- •Задачі на збільшення (зменшення) числа на декілька одиниць, сформульовані у непрямій формі .
- •Задачі, що утримують величини: швидкість, час, відстань.
- •Задачі на час.
- •Види складених задач 4-го класу Задачі на знаходження четвертого пропорційного. Спосіб відношень.
- •Розв’язання
- •Задачі на подвійне наведення до одиниці
- •Задачі на спільну роботу.
- •Задачі на одночасний рух в різних напрямках
- •Пам’ятка ( 1 спосіб: s, V )
- •3) Задачі на знаходження часу.
- •Пам’ятка ( 2 спосіб: s, V, t )
- •Задачі на рух в одному напрямку
- •Задачі на неодночасний рух в різних напрямках
- •Задачі на рух за течією та проти течії річки
- •Задачі на пропорційне ділення
- •Четвертою дією ми дізнаємося про масу вугілля ,яку було привезено другого дня.
- •Задачі на знаходження невідомого за двома різницями
- •Задачі на знаходження середнього арифметичного
- •Задачі, які містять дроби Задачі на знаходження дробу від відомого числа.
- •Складені задачі, які містять знаходження дробу від невідомого числа.
- •6 Пачок по 50 шт.
- •Алгебраїчний матеріал в курсі математики 4-го класу
- •Геометричні фігури та величини.
- •Геометричні тіла
- •Методика вивчення величин в 4-му класі
- •Площа фігури
- •2. Основні питання методики вивчення теми. Введення поняття “Площа фігури”
- •Нестандартні задачі для 4-го класу
- •Задачі, що розв’язуються арифметичним методом.
- •Задачі, що розв’язуються „з кінця”
- •Задачі на комбінації чисел
Задачі на рух за течією та проти течії річки
Задачі на рух за течією та проти течії річки спираються на поняття: власна швидкість катера ( Vвласна) , швидкість течії річки( Vтечії), швидкість катера за течією річки ( Vза течією) та швидкість катера проти течії річки ( Vпроти течії). Отже, ці поняття слід ввести, познайомити учнів з відповідними формулами та показати учням як виконується креслення до подібних задач.
Познайомити учнів з даними поняттями можна залучивши досвід дітей по спостереженню за рухом маленького паперового кораблика у річці. Діти згадують:
Коли кораблик пливе за течією річки, то течія річки, йому допомагає, підштовхує, тому його швидкість збільшується:
Vтечії
Vза
течією
= Vвласна
+ Vтечії

Vвласна



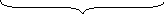

Коли кораблик пливе проти течії річки, то течія йому перешкоджає, гальмує, тому його швидкість зменшується:
Vтечії
Vза
течією
= Vвласна
- Vтечії


Vвласна



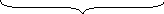

Задача. Відстань між двома пристанями по річці 180 км. За який час катер пройде цю відстань туди й назад, якщо швидкість катера в стоячій воді
15
![]() ,
а швидкість течії річки 3
,
а швидкість течії річки 3![]() ?
?
Про що йде мова в задачі? ( Про рух катера в стоячій воді, за течією та проти течії річки.)
Отже, можна цю задачу розбити на три частини:
розглянути рух катера за течією річки;
розглянути рух катера проти течії річки; виходячи з другої та першої частин відповісти на перше запитання задачі.
Які висновки можна зробити ?
При русі катера за течією річки, течія ніби підштовхує катер і його швидкість збільшується на швидкість течії;
При русі проти течії річки, течія заважає руху катера, його швидкість зменшується на швидкість течії.
Зробимо креслення.
1
За
коротким записом поясніть числа задачі.
( Число 15 означає власну швидкість
катера. 15
![]() означає, що катер при працюючому двигуні
за кожну годину проходить по 15 км.
означає, що катер при працюючому двигуні
за кожну годину проходить по 15 км.
3
![]()
1
 5
5![]()





180 км
Число
3 означає швидкість течії річки. 3
![]() означає, що якщо вимкнути двигун катера,
то він рухатиметься тільки за течією,
долаючи за кожну годину по 3 км. Число
180 означає відстань між пристанями.
означає, що якщо вимкнути двигун катера,
то він рухатиметься тільки за течією,
долаючи за кожну годину по 3 км. Число
180 означає відстань між пристанями.
3
![]()
1
 5
5![]()





180 км
Назвіть запитання задачі. (За який час катер пройде цю відстань туди й назад?)
Що треба знати, щоб на нього відповісти? ( Потрібно знати два числові значення: 1 – час руху катера за течією , невідомо, та П – час руху катера проти течії річки.)
Якою арифметичною дією відповімо на запитання задачі? ( Дією додавання.)
Чи можна відразу відповісти на запитання задачі? ( Ні, ми не знаємо обидва числові значення.)
Що треба знати, щоб дізнатися про час руху катера за течією? (Треба знати два числові значення: 1 – відстань, яку пройшов катер за течією, відомо 180 км, та П – швидкість катера за течією, невідомо .)
Якою арифметичною дією відповімо на це запитання? ( Дією ділення.)
Чи можна одразу відповісти на це запитання? (Ні, невідома швидкість катера за течією річки. )
Що треба знати, щоб про це дізнатися? ( Треба знати два числові значення: 1 – власну швидкість катера, відомо 15
 ,
та П – швидкість течії річки, відомо 3
,
та П – швидкість течії річки, відомо 3 )
)Якою арифметичною дією відповімо на це запитання? ( Дією додавання.)
Чи можна тепер відповісти на запитання задачі? ( Ні, ми не знаємо час руху катера проти течії річки.)
Що треба знати, щоб про це дізнатися? ( Треба знати два числові значення: 1 – власну швидкість катера, відомо 15
 ,
та П – швидкість течії річки, відомо 3
,
та П – швидкість течії річки, відомо 3 )
)Якою арифметичною дією відповімо на це запитання? ( Дією віднімання.)
Чи можна тепер відповісти на запитання задачі. ( Так, ми від запитання перейшли до числових даних. Аналіз закінчено.)

?



? + ?








180 : ? 180 : ?








15 + 3 15 - 3
Складіть план розв’язування задачі. ( Першою дією дізнаємось про швидкість катера за течією річки. Другою дією дізнаємось про час руху катера за течією річки. Третьою дією дізнаємось про швидкість катера проти течії річки. Четвертою дією дізнаємось про час руху катера проти течії річки. П’ятою дією дізнаємось про загальний час руху катера туди і назад.)
Запишіть розв’язання по діях з поясненням.
1)
15 + 3 = 18 (![]() )
– швидкість катера за течією;
)
– швидкість катера за течією;
2) 180 : 18 = 10 (год) – час руху катера за течією;
3)
15 – 3 = 12 (![]() )
– швидкість руху катера проти течії;
)
– швидкість руху катера проти течії;
4) 180 : 12 = 15 ( год) – час руху катера проти течії річки;
5) 10 + 15 = 25 ( год) – загальний час руху катера за течією та проти течії річки;
Відповідь: 25 год потрібно катеру, щоб подолати відстань туди і назад.
Задача . По озеру човен пройшов за 20 хв 8 км, а коли ввійшов у річку, то за 2 год пройшов 42 км. Знайди швидкість течії річки ( мотор працював увесь час однаково.)
Розв’язання
8км = 8000 м; 42 км = 42000 м; 2 год = 120 хв.
8000 : 20 = 200 (
 )
– швидкість човна по озеру, власна
швидкість човна;
)
– швидкість човна по озеру, власна
швидкість човна;42000 : 120 = 350 (
 )
– швидкість човна за течією річки;
)
– швидкість човна за течією річки;350 – 200 = 150 (
 )
– швидкість течії річки
)
– швидкість течії річки
Відповідь:
150
![]() .
.
При розв’язанні цієї задачі ми скористалися формулою знаходження швидкості течії річки. Виведемо можливі формули знаходження швидкості течії річки.
В формулі:
Vза
течією
= Vвласна
+ Vтечії
Сума 1 доданок 2 доданок
Швидкість течії – це другий доданок. Щоб знайти другий доданок, треба від суми відняти перший доданок. Отже маємо:
Vтечії
=
Vза
течією
- Vвласна
В формулі:
Vпроти
течії
= Vвласна
- Vтечії
Різниця Зменшуване Від’ємник
Швидкість течії – це від’ємник. Щоб знайти невідомий від’ємник, треба від зменшуваного відняти різницю. Отже, маємо:
Vтечії
=
Vвласна
-
Vпроти
течії
Складнішою є задача на знаходження швидкості течії за відомими швидкістю за течією річки та швидкістю проти течії річки.
Задача.
Швидкість руху човна за течією річки
а
![]() ,
а швидкість човна проти течії річкив
,
а швидкість човна проти течії річкив
![]() .Знайти
швидкість течії.
.Знайти
швидкість течії.
Vвласна











Vпроти течії Vтечії
Vвласна Vтечії









Vза
течією
= а
![]()
З малюнка бачимо, що швидкість човна за течією більше швидкості човна проти течії на подвійну швидкість течії. Тому маємо формулу:
Vтечії
=
(Vза
течією
– Vпроти
течії
) : 2
