З двох дробів з рівними знаменниками

більший той, у якому чисельник більший.

• Запиши цей висновок у загальному вигляді.

Якщо а>в, то >.

• Запиши кілька дробів з однаковими знаменниками і розташуй їх в порядку спадання.

• Як змінюються чисельники? Як змінюються дроби?

• Який висновок можна зробити?

З двох дробів з рівними знаменниками

менший той, у якому чисельник менший.

• Запиши цей висновок в загальному вигляді.

Якщо а<в, то <.

• Поєднайте обидва висновки у один.

З двох дробів з однаковими знаменниками той,

у якого чисельник .

Завдання 4. Запиши дроби, в яких: чисельник 2, знаменник 5; чисельник 4, знаменник 6; чисельник 4, знаменник 10; чисельник 1, знаменник 7.

• Чи можна порівняти ці дроби за величиною користуючись зробленим висновком? Поясни відповідь.

• Для кожного записаного дробу запиши кілька дробів, з якими їх зручно порівнювати. Розташуй кожну групу дробів в порядку зростання величини дробів.

Завдання 5. Накресли відрізок довжиною 6 см. Розділи його на 12 рівних частин. Покажи цього відрізку.

• Скільки таких частин містить .

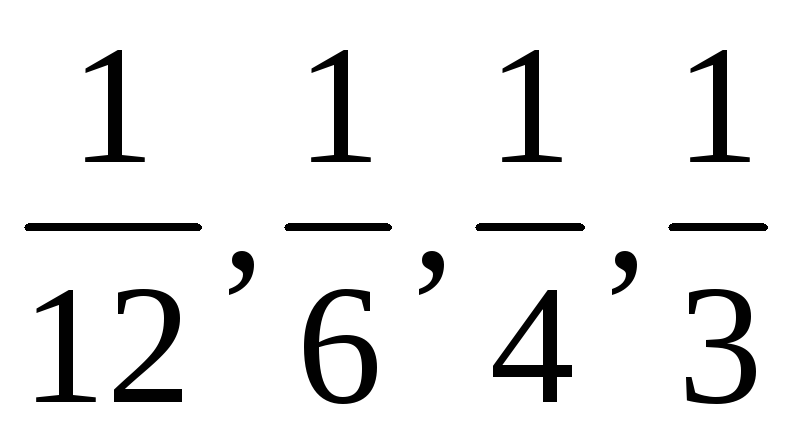• Порівняй дроби .

Міркуємо так: цілу величину спочатку поділили на 12 рівних частин, а потім на 3 рівні частини, величина частини менше, ніж величиначастини, тому величина< . Згадуємо висновок, який було зроблено при вивченні частин:

Чим на більше число рівних частин поділене ціле, тим менше величина кожної частини.

Завдання 6. Розглянь дроби:

Чим вони схожі? Чим відрізняються?

• Випиши спочатку найменший дріб, а потім найбільший. Як ти дізнався, який дріб найменший? А найбільший?

• Запиши всі дані дроби в порядку зростання.

Завдання 7. Порівняй дроби та ; та .

Міркуємо так: цілу величину спочатку поділили на 6 рівних частин, а потім на 3 рівні частини, величина частини менше, ніж величина частини, тому величина < .

Завдання 8. Чим схожі і чим відрізняються дроби:

?

• Яка з них найменша? Підкресли її однією рискою. Яка з них найбільша? Підкресли її двома рисками. Поясни відповідь.

• Як в них змінюються знаменники? Як змінюються дроби?

• Який висновок можна зробити?

Якщо у дробів однакові чисельники та різні знаменники, то більший той дріб, в якого знаменник менший.

Завдання 9. В якому порядку записані наступні дроби:

?

• Що спільного в цих дробах? Чим вони відрізняються?

• Як змінюються знаменники? Як змінюються дроби?

• Який висновок можна зробити?

У дробів однакові чисельники та різні знаменники, то менший той дріб, в якого знаменник більший.

• Поєднайте обидва висновків в один.

З двох дробів з однаковими чисельниками той, у якого знаменник .

Завдання 10. Запиши дроби в порядку зростання( спадання): ; ; ; ; .

Завдання 11.Порівняй дроби: .

Завдання 12. Порівняй дроби:

та та тата.

Завдання 13. Порівняй дроби:

А)

Б)

Завдання 14. Записати дроби у порядку зростання: .

• За яким принципом складені ці дроби? (Чисельник кожного дробу на 1 менший за його знаменник.)

• Яким дробом можна доповнити кожний дріб до 1? Запишіть відповідні дроби під кожним з даних дробів.

Д

роби у нижньому рядку зручно порівнювати, тому що в них рівні чисельники. Найменший з них дріб, найбільший. Чим меншу частину ми віднімемо з 1, тим більше буде решта. Тому в порядку зростання ці дроби вишукуються наступним чином:.

Завдання 15. При яких натуральних значеннях змінної вірна нерівність:

> > >

Завдання 16. Які значення можуть приймати змінні х та у щоб нерівності були вірними:

а) б)

в) г)

Завдання 17. Запиши множину дробів , якщо відомо, що:

а) 3 < x 4 , 6 y 8; б) 9 < x < 12 , 18 < y < 20.

Порівняй ці дроби.

Завдання 18. Знайди 3 значення змінної t, які задовольняють нерівності:

а) 1 < t < 5 б) t

Завдання 19. Розташуй дроби в порядку зростання:,,,,,,.

• Яка найбільше число у знаменнику? ( 8.)

• Що вона показує? ( На скільки рівних частини поділили , наприклад відрізок. Відрізок поділили на 8 рівних частин.)

• Що покає чисельник? ( Скільки взяли рівних частин.)

• Накресли три відрізка довжиною 8 см і похилу лінію. Перший відрізок розділи на дві рівні частини. Кожна частина цього відрізка містить 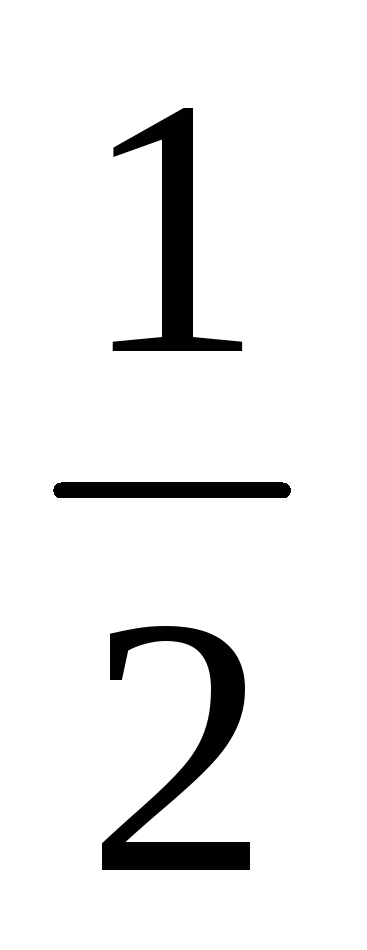відрізка. Другий відрізок розділи на чотири рівні частини. Кожна частина містить відрізка. Третій відрізок поділи на 8 рівних частин. Кожна частина містить відрізка.

• Проведи пунктирні лінії на похилу. Починай по порядку з тих дробів, які записані вище. Точки можна відмічати кольоровим олівцем. Отже, починай з 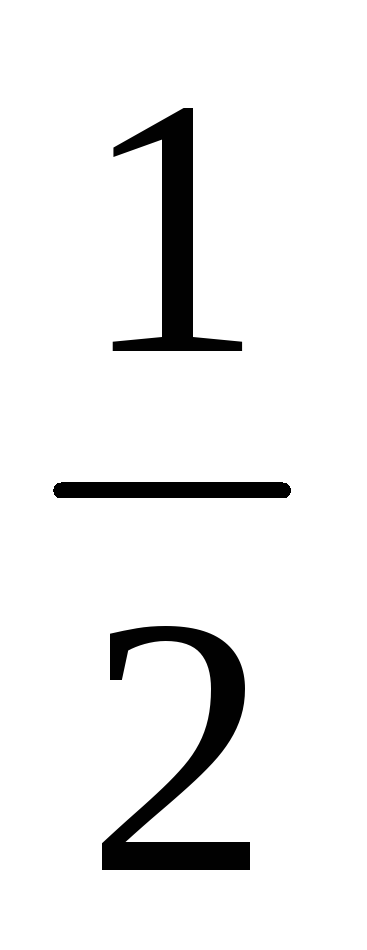,, і так далі.

Відмітивши точки на похилій, учні наочно уявляють дроби в порядку зростання і записують їх в наступному порядку : ,,,,,,.

Завдання 20. За таким кресленням порівняти дроби. та,та.

Завдання 21. За допомогою креслення ( накресли два відрізка, довжиною 6 см = 12 клітинок) відповіси на запитання:

1. Що більше 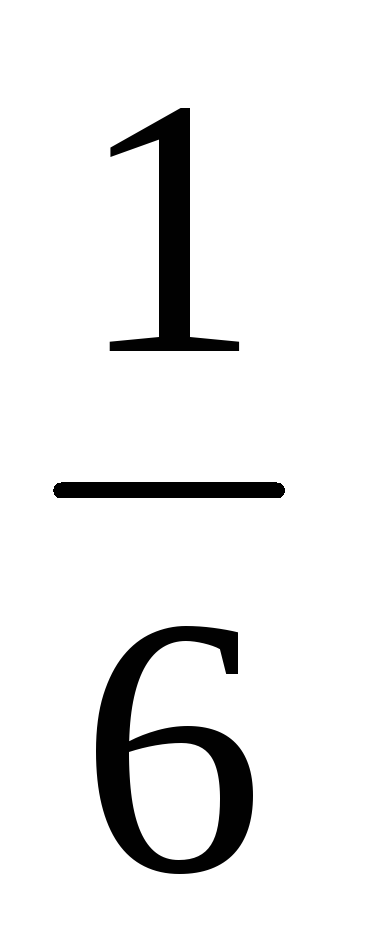або?

2. Як з отримати?

3. Скільки в?

4. Скільки в шостих частин?

Завдання 22. Розглянь дроби: . Як вони пов’язані між собою?

• Накресли відрізок довжиною 12 см і відміть на ньому дроби. Скільки різних точок ти отримав?

• Подумай і поясни, чому ти отримав лише одну точку?

• Чи можна стверджувати, що ці дороби рівні одна одній?

• Чи вірно таке міркування: - це половина ітеж половина, тому що розділили на 4 рівні частини і взяли половину таких частин.

• Проведи таке міркування для дробів та.

• Розглянь даний рядок дробів. Порівняй чисельники першого та другого дробу. Як в них змінився чисельник? Порівняй їх знаменники. А як змінився знаменник? Таку саму роботу проведи з першим та третім дробами....

• Що цікавого ти помітив? Як змінюються чисельник і знаменник в кожному дробу? За цим правилом запиши ще кілька дробів, які будуть рівні даним.

• Одночасно помноживши і чисельник і знаменник на одне й те саме число, запиши як можна більше дробів, що дорівнюють .

Завдання 23. Порівняй дроби кожної пари:

• Що ти можеш про них сказати? Постав між цими дробами знак порівняння.

• Чи вірно твердження: Дроби кожної пари рівні між собою?

• Порівняй чисельники дробів кожної пари та їх знаменники. У скільки разів чисельник другого дробу більший за чисельник першого? А знаменник? Зроби висновок.