32.4. Критерии согласия Пирсона и Колмогорова

Критерием согласияназывается критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Пусть по выборке объема nполучено эмпирическое распределение:

Варианта	x1	x2	…	xm
Эмпирическая (наблюдаемая) частота	n1	n2	…	nm

По данным наблюдения выдвигают гипотезу о законе распределения генеральной совокупности, например, предполагают, что генеральная совокупность распределена равномерно или нормально. Затем для тех же объектов, которые попали в выборку, вычисляют частоты, исходя уже из теоретической гипотезы. В результате получают частоты (их называют выравнивающими частотами), которые, вообще говоря, отличаются от наблюдавшихся. Для того чтобы определить, правильно или нет выдвинута гипотеза (т. е. случайны ли расхождения наблюдавшихся и выравнивающих частот или эти расхождения являются следствием неправильной гипотезы) применяюткритерии согласия эмпирических наблюдений выдвинутой гипотезе. Име­ются несколько критериев согласия:(«хи квадрат») Пирсона, Колмогорова, Смирнова и др. Познакомимся с критерием согласия Пирсона.

Предположим, что на основе приведенного выше распределения выдвинута гипотеза: генеральная совокупность имеет нормальное распределение.

Алгоритм применения критерия Пирсона

1.Вычисляются выборочная средняяи выборочное среднее квадратическое отклонение

2.Вычисляются теоретические частоты

где n– объем выборки (сумма всех частот);

h– шаг (разность между двумя соседними вариантами);

3.Сравниваются эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:

а) составляется расчетная таблица, по которой находят наблюдаемое значение критерия

б) по таблице критических точек распределения (прил. 7), по заданному уровню значимостии числу степеней свободы(s– число групп выборки) находится критическая точкаправосторонней критической области.

Если – нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно). Если– гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.

Заметим, что малочисленные частоты следует объединить. В этом случае и соответствующие им теоретические частоты тоже надо сложить. При условии объединения частот, для определения числа степеней свободы по формулеследует в качествеsпринять число групп выборки, оставшихся после объединения частот.

Пусть эмпирическое распределение задано в виде последовательности интервалов и соответствующих им частотn_i(n_i– сумма частот вариант, которые попали вi-й интервал):

		…
		…

Проверка гипотезы о нормальном распределении

генеральной совокупности X

Чтобы при уровне значимости проверить гипотезу о нормальном распределении генеральной совокупности, необходимо реализовать следующий алгоритм.

1.Вычислить выборочную среднююи выборочное среднее квадратическое отклонениепричем в качестве вариантпринять среднее арифметическое концов интервала:

2.ПронормироватьX, т. е. перейти к случайной величинеи вычислить концы интервалов:причем наименьшее значениеZ, т. е.положить равныма наибольшее, т. е.– равным

3.Вычислить теоретические частоты

где n– объем выборки (сумма всех частот);

–вероятности попадания Xв интервалы

–функция Лапласа.

4.Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого надо:

а) составить расчетную таблицу, по которой можно найти наблюдаемое значение критерия Пирсона

б) по таблице критических точек распределения (прил. 7), по заданному уровню значимостии числу степеней свободы(s– число интервалов выборки) найти критическую точку правосторонней критической области

Если – нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Если– гипотезу отвергают.

Заметим, что интервалы, содержащие малочисленные эмпирические частоты следует объединить, а частоты этих интервалов сложить. При условии объединения интервалов для определении числа степеней свободы по формулеследует в качествеsпринять число интервалов, оставшихся после объединения интервалов.

Рассмотрим вопрос проверки гипотезы о показательном распределении генеральной совокупности.

Пусть задано эмпирическое распределение непрерывной случайной величины Xв виде последовательности интервалови соответствующих им частотn_i– объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величинаXимеет показательное распределение.

Чтобы при уровне значимости проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо выполнить следующие действия:

1.Найти по заданному эмпирическому распределению выборочную среднююприняв в качестве «представителя»i-го интервала его середину

2.Принять в качестве оценки параметрапоказательного распределения величину, обратную выборочной средней,

3.Найти вероятности попаданияXв интервалыпо формуле

4.Вычислить теоретические частоты

где – объем выборки.

5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы гдеs – число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s – число интервалов, оставшихся после объединения.

Проверка гипотезы о распределении генеральной

совокупности по биномиальному закону

Пусть произведено nопытов. Каждый опыт состоит изNнезависимых испытаний, в каждом из которых вероятность появления событияAодна и та же. Число появлений событияAв каждом опыте регистрируется. В результате получим следующее распределение дискретной случайной величиныX– числа появлений событияA:

	0	1	2	…
	0	1	2	…

В первой строке указано число x_iпоявлений событияAв одном опыте. Во второй строке – частотаn_iпоявлений событияA.

Необходимо с помощью критерия Пирсона проверить гипотезу о распределении дискретной случайной величины Xпо биномиальному закону.

Чтобы при уровне значимости проверить гипотезу о том, что дискретная случайная величинаXраспределена по биномиальному закону, необходимо реализовать следующий алгоритм.

1.Найти по формуле Бернулли вероятностиP_iпоявления ровноiсобытийAвNиспытаниях (i = 0, 1, 2, …,s, гдеs– максимальное число наблюдавшихся появлений событияAв одном опыте, т. е.

2.Найти теоретические частоты

где n– число опытов.

3. Сравнить эмпирические и теоретические частоты по критерию Пирсона, приняв число степеней свободы(при этом предполагается, что вероятностьpпоявления событияAзадана, т. е. не оценивалось по выборке и не производилось объединение малочисленных частот).

Если же вероятность pбыла оценена по выборке, тоЕсли, кроме того, было произведено объединение малочисленных частот, тоs– число групп выборки, оставшихся после объединения частот.

Проверка гипотезы о равномерном распределении

генеральной совокупности

Пусть имеется эмпирическое распределение непрерывной случайной величины Xв виде последовательности интервалови соответствующих им частотn_i– объем выборки). Необходимо с помощью критерия Пирсона проверить гипотезу о равномерном распределении случайной величиныX.

Чтобы проверить гипотезу о равномерном распределении X, т. е. по закону

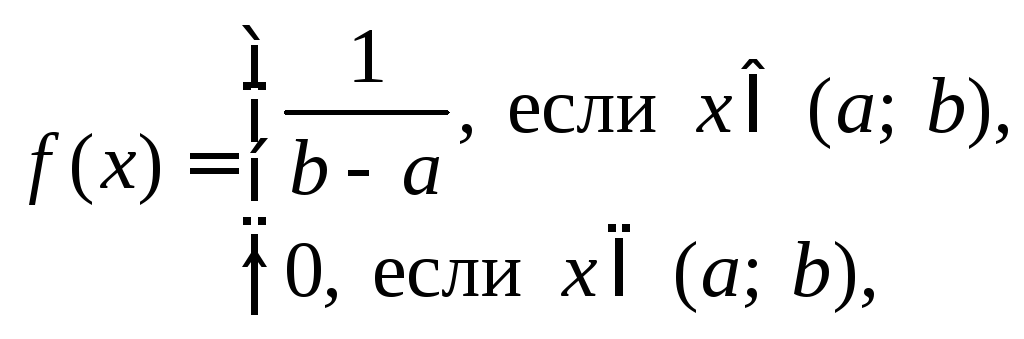
необходимо реализовать следующий алгоритм.

1.Оценить параметрыaиb– концы интервала, в котором наблюдались возможные значенияX, по формулам

2.Найти плотность вероятностей предполагаемого распределения

3.Найти теоретические частоты:

4.Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободыгдеs– число интервалов, на которые разбита выборка.

Проверка гипотезы о распределении генеральной

совокупности по закону Пуассона

Чтобы при уровне значимости проверить гипотезу о том, что случайная величинаXраспределена по закону Пуассона, необходимо реализовать следующий алгоритм.

1.Найти по заданному эмпирическому распределению выборочную среднюю

2.Принять в качестве оценки параметрараспределения Пуассона выборочную среднюю

3. Найти по формуле Пуассона (прил. 3) вероятности P_i появления ровно i событий в n испытаниях (i = 0, 1, 2, …, r, где r – максимальное число наблюдавшихся событий; n – объем выборки).

4.Найти теоретические частоты по формуле

5.Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободыs– число различных групп выборки (если производилось объединение малочисленных частот в одну группу, тоs– число оставшихся групп выборки после объединения частот).

Если закон распределения признака Xс непрерывной вариацией известен (т. е. вид функции и числовые значения параметров известны), то можно применятькритерий согласия Колмогорова. При его использовании сравниваются эмпирическаяи гипотетическая (предполагаемая)функции распределения. Отметим, что критерий Колмогорова применяется для проверки гипотез о законах распределения только непрерывных случайных величин.

Критерий Колмогорова проверки гипотезы о виде закона распределения является наиболее простым, однако этот критерий можно применять только в том случае, когда гипотетическое распределение полностью известно, т. е. когда известен не только вид функции распределенияно и все входящие в нее параметры.

Общий алгоритм применения критерия Колмогорова может быть сформулирован следующим образом.

Пусть из генеральной совокупности с функцией распределения произведена выборка объемомn

1.Результаты выборки представить в виде интервального ряда или расположить в возрастающем порядке.

2.Найти эмпирическую функцию распределения

где – накопленная частота.

3. Вычислить значения предполагаемой теоретической функции распределения по данным выборки.

4.Для каждого значенияx_iвычислить

5.Вычислить наблюдаемое значение выборочной статистикиКолмогорова

6.По заданному уровню значимостииз таблицы критических значений распределения Колмогорова (прил. 9) найти

7.Еслито наблюдаемые данные хорошо согласуются с теоретическим распределением; еслито проверяемая гипотеза отклоняется.

Пример 1. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

Эмпирическая частота	6	13	38	74	106	85	30	14
Теоретическая частота	3	14	42	82	99	76	37	13

Решение. Вычислим для чего составим расчетную таблицу:

i	ni
1	6	3	3	9	3
2	13	14	–1	1	0,07
3	38	42	–4	16	0,38
4	74	82	–8	64	0,78
5	106	99	7	49	0,49
6	85	76	9	81	1,07
7	30	37	–7	49	1,32
8	14	13	1	1	0,08


Найдем число степеней свободы, учитывая, что число различных вариант Имеем:По уровню значимостии числу степеней свободыпо таблице значений(прил. 7) найдем:Так какнет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности.

Пример 2. Даны 100 значений температуры масла двигателя БелАЗ при средних скоростях:

Предполагая, что наблюдаемая случайная величина X распределена по нормальному закону, записать гипотетическую функцию распределения случайной величины X. Найти теоретические частоты нормального распределения и проверить согласие гипотетической функции распределения с нормальным законом с помощью критерия согласия (уровень значимости принять равным

Решение. Температура масла в двигателе является непрерывной случайной величиной. Обозначим ее X.

Для построения интервального статистического ряда выберем наибольшее и наименьшееиз имеющихся значений случайной величиныX:

Диапазон имеющихся значений разобьем на 6 частичных интервалов длины h. Разбиение произведем так, чтобы было серединой первого частичного интервала,– серединой последнегоk-го интервала. Очевидно, длина отрезка будет равнойОтсюда находим

Взяв начальную точку равной получим частичные интервалы [45; 47), [47; 49), [49; 51), …, [55; 57). Подсчитаем для каждого интервала частотыn_i. Построим интервальный статистический ряд частот случайной величины X.

xi	[45; 47)	[47; 49)	[49; 51)	[51; 53)	[53; 55)	[55; 57)
ni	4	13	34	32	12	5

–число выборочных значений случайной величины X.

Вычислим точечные оценки параметров нормального распределения.

Для вычисления воспользуемся формулой

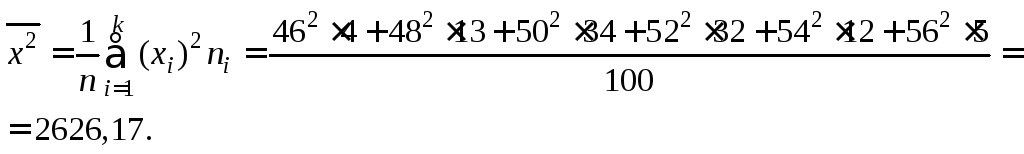
Запишем функцию распределения нормального закона

Вычислим вероятности P_i попадания значений рассматриваемой CB X с функцией распределения вi-й частичный интервал и теоретические частоты . Значения функциивозьмем из таблицы значений функции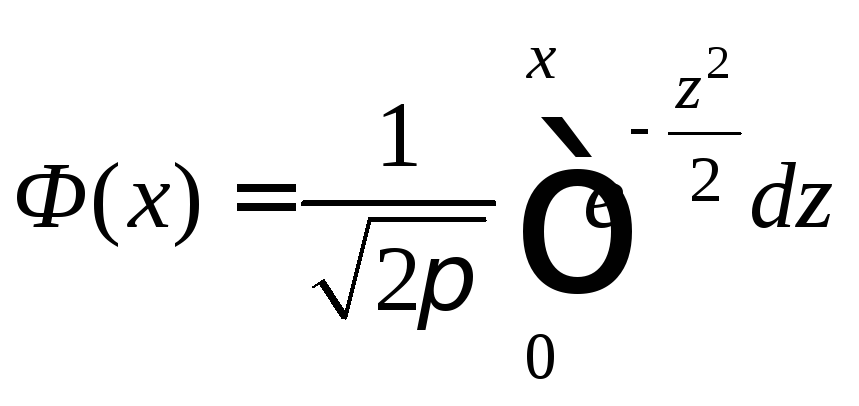(прил. 2). Контролируем выполнение неравенстваЭто необходимо для того, чтобы обеспечить близость закона распределенияχ²-статистики Пирсона к χ²-распределению.

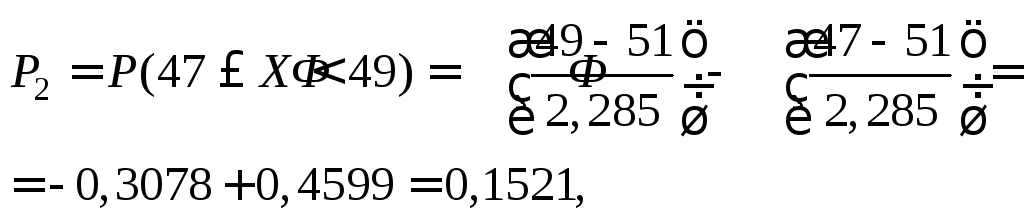
Найдем χ²-статистику Пирсона:

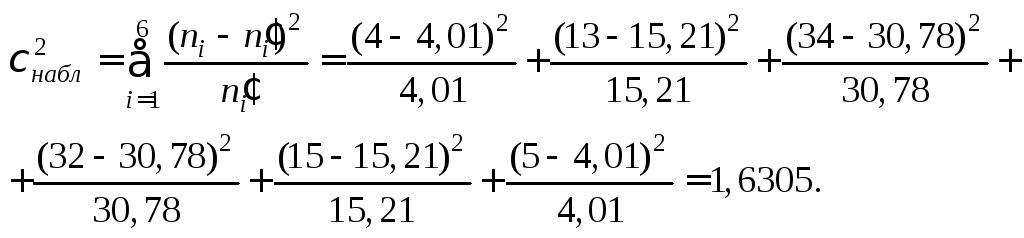
По таблице значений (прил. 7) – распределения по уровню значимостии числу степеней свободывыберем значениеСравним вычисленное значениесПосколькуто гипотеза о нормальном распределении температуры масла с параметрамисогласуется с опытными данными.

Пример 3. Дана выборка объемом извлеченная из генеральной совокупностиX:

xi	2	4	6	8	10	12
ni	1	2	2	2	2	1

При уровне значимости проверить с помощью критерия Колмогорова гипотезу о равномерном распределении генеральной совокупностиX в интервале (2; 12).

Решение. Гипотетическая функция распределения

По данным выборки найдем иво всех точкахx_i и оценим Результаты вычислений сведем в таблицу:

i	xi	ni
1	2	1	0,0	0	0
2	4	2	0,1	0,2	0,1
3	6	2	0,3	0,4	0,1
4	8	2	0,5	0,6	0,1
5	10	2	0,7	0,8	0,1
6	12	1	0,9	1,0	0,1

Вычислим:

По заданному уровню значимости найдем(прил. 9).

Так как то предположение о равномерном распределении генеральной совокупности не отвергается.

Задания