
- •31. Теория вероятностей
- •31.1. Основные понятия теории вероятностей.
- •I уровень
- •II уровень
- •III уровень
- •31.2. Теоремы сложения и умножения вероятностей
- •I уровень
- •II уровень
- •III уровень
- •31.3. Формула полной вероятности. Формула Байеса
- •I уровень
- •II уровень
- •III уровень
- •31.4. Повторение испытаний
- •I уровень
- •II уровень
- •III уровень
- •31.5. Дискретные случайные величины. Функция
- •I уровень
- •II уровень
- •31.6. Непрерывные случайные величины
- •I уровень
- •II уровень
- •III уровень
- •31.7. Основные законы распределения
- •I уровень
- •II уровень
- •III уровень
- •31.8. Функция одного случайного аргумента
- •I уровень
- •II уровень
- •III уровень
- •31.9. Функция двух случайных аргументов
- •I уровень
- •II уровень
- •III уровень
- •31.10. Закон больших чисел
- •I уровень
- •II уровень
- •III уровень
- •32. Математическая статистика
- •32.1. Основные понятия математической
- •I уровень
- •II уровень
- •III уровень
- •32.2. Точечные и интервальные оценки
- •I уровень
- •II уровень
- •III уровень
- •32.3. Статистическая проверка
- •I уровень
- •II уровень
- •III уровень
- •32.4. Критерии согласия Пирсона и Колмогорова
- •I уровень
- •II уровень
- •III уровень
- •32.5. Элементы теории корреляции. Выборочное
- •I уровень
- •II уровень
- •III уровень
31. Теория вероятностей
31.1. Основные понятия теории вероятностей.
Элементы комбинаторики
Всякое осуществление определенного комплекса условий или действий, при которых наблюдается соответствующее явление, называют опытомилииспытанием(например, опытом являются стрельба по мишени, бросание монеты, бросание игральной кости, т. е. кубика с нанесенным на каждую грань числом очков – от одного до шести).
Возможный результат, исход опыта называется событием. Например, при стрельбе по мишени событием будет попадание или промах, при бросании монеты – герб или цифра на ее стороне и т. д.
Для обозначения событий используются большие буквы латинского алфавита: A,B,C,Dи т. д.
Событие называется
достовернымв данном опыте, если
оно обязательно произойдет в этом опыте.
Достоверное событие обозначают![]() .
.
Событие называется
невозможным, если в данном опыте
оно не может произойти. Невозможное
событие обозначают
![]()
Событие называется случайнымпо отношению к данному опыту, если при осуществлении этого опыта оно может наступить, а может и не наступить.
З а м е ч а н и е 1. Одно и то же событие в некотором опыте может быть достоверным, в другом – невозможным, в третьем – случайным.
Суммой событийAиBназывается третье событиеA+B, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий:AилиB.
Если наступление события обозначать знаком «+», а ненаступление – знаком «–», то полную характеристику будет давать следующая таблица:
|
A |
B |
A + B |
|
+ |
+ |
+ |
|
+ |
– |
+ |
|
– |
+ |
+ |
|
– |
– |
– |
Аналогично определяется сумма трех, четырех и т. д. событий. Вообще, сумма любого множества событий есть событие, которое наступает в тех и только тех случаях, когда наступает хотя бы одно из событий данного множества.
Произведением событийAиBназывается третье событиеAB, которое наступает тогда и только тогда, когда наступают оба события:AиB.
Полную характеристику события AB дает следующая таблица:
|
A |
B |
AB |
|
+ |
+ |
+ |
|
+ |
– |
– |
|
– |
+ |
– |
|
– |
– |
– |
Аналогично определяется произведение любого множества событий.
Событием,
противоположным событиюA,
называется событие![]() которое наступает тогда и только тогда,
когда не наступает событиеА.
которое наступает тогда и только тогда,
когда не наступает событиеА.
Противоположное событие можно определить следующей таблицей:
|
А |
|
|
+ |
– |
|
– |
+ |
События AиBназываютсяравными, если каждый раз, когда наступает одно из них, наступает и другое.
Равенство событий AиBзаписываютA=B.
Для наглядного истолкования соотношений между событиями удобно использовать так называемые диаграммы Эйлера–Венна. Каждое событие в этом случае рассматривается как попадание случайно брошенной точки в некоторую область на плоскости, т. е. каждое событие задается некоторой фигурой на плоскости.
При
таком толковании, событие A
+ B
будет не что иное, как попадание точки
в объединение фигур A
и B
(рис. 31.1), событие AB –
попадание в область, являющуюся
пересечением фигур A
и B,
а событие
![]() – попадание в область, дополнительную
к фигуреA.
– попадание в область, дополнительную
к фигуреA.
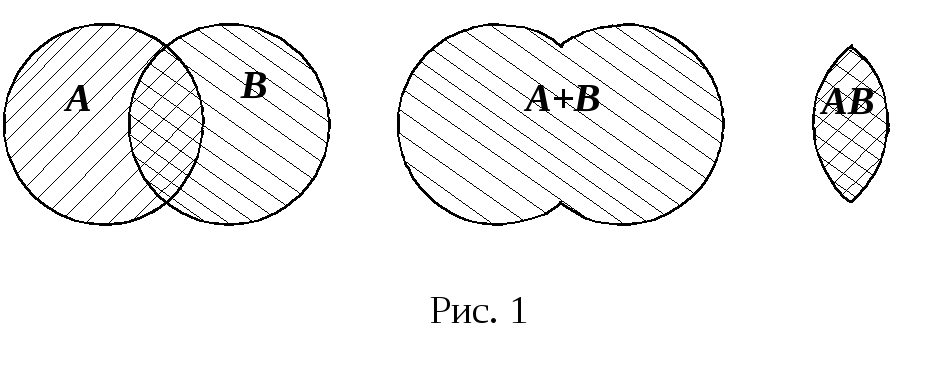
Рис. 31.1
Пусть А–
случайное событие по отношению к
некоторому опыту. Если произведеноNопытов и при этом событиеАнаступило
вNAслучаях, то отношение![]() называетсяотносительнойчастотойсобытияАв данной
серии опытов.
называетсяотносительнойчастотойсобытияАв данной
серии опытов.
Длительные наблюдения показывают, что если в одинаковых условиях производятся опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа.
Вероятностью случайного событияАназывается числоP(A), около которого колеблется относительная частота этого события в длинных сериях опытов.
Приведенное выше определение часто называют «статистическим определением» вероятности.
Так как частота
![]() удовлетворяет условиям
удовлетворяет условиям![]() то в тех же пределах заключена и
вероятность любого события:
то в тех же пределах заключена и
вероятность любого события:
![]()
При этом, если
событие Адостоверное (т. е.
наступает при каждом осуществлении
опыта), тоNA = Nи, значит,
![]() = 1;
тем самымвероятность достоверного
события равна единице.
В другом
крайнем случае, когда событиеAневозможно:NA = 0
и, значит,
= 1;
тем самымвероятность достоверного
события равна единице.
В другом
крайнем случае, когда событиеAневозможно:NA = 0
и, значит,
![]() = 0.
Значит,вероятность невозможного
события равна нулю.
= 0.
Значит,вероятность невозможного
события равна нулю.
События А,В,Сназываютсянесовместными, если два из них не могут произойти в данном опыте вместе.
События А,В,Сназываютсясовместными, если в данных условиях появление одного из этих событий не исключает появление другого при этом же испытании.
Если сумма событий
![]() – достоверное событие, т. е.
– достоверное событие, т. е.![]() то говорят, что события
то говорят, что события![]() образуютполную группу событий
для данного опыта.
образуютполную группу событий
для данного опыта.
Если события
![]() обладают свойствами:
обладают свойствами:
1)
![]()
2)
![]() при
при
![]()
то говорят, что они образуют полную группу попарно несовместных событий.
Если
![]() – полная группа попарно несовместных
событий, связанных с некоторым испытанием,
то события
– полная группа попарно несовместных
событий, связанных с некоторым испытанием,
то события![]() называютэлементарными событиями.
называютэлементарными событиями.
Событие А называется благоприятствующим событию В, если наступление события А влечет за собой наступление события В.
Исторически первым было классическое определение вероятности.
Вероятностью события Аназывается отношение числа элементарных событий, благоприятствующих событиюА, к числу всех равновозможных элементарных событий опыта, в котором может появиться событиеА.
В соответствии с классическим определением вероятности
![]() (31.1)
(31.1)
где m– число элементарных событий, благоприятствующих событиюA;
n– число элементарных событий, образующих полную группу равновозможных и попарно несовместных событий.
Классическое определение вероятности предполагает, что число всех элементарных событий конечно. Но на практике часто встречаются опыты, для которых множество таких событий бесконечно.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Пусть на плоскости задана квадрируемая область G, т. е. область, имеющая площадь. Площадь этой области обозначим черезSG. В областиGсодержится областьgплощадиSg(рис. 31.2).
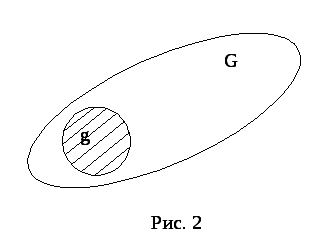
Рис. 31.2
В область Gнаудачу брошена точка. Считают, что брошенная точка может попасть в некоторую часть областиGс вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. ЕслиA– попадание брошенной точки в областьg, то геометрическая вероятность этого события определяется формулой
![]()
Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область объема VG, содержащую областьgобъемаVg:
![]()
Часто приходится составлять из конечного числа элементов различные комбинации и производить подсчет числа всех возможных комбинаций, составленных по некоторому правилу. Такие задачи называются комбинаторными, а раздел математики, занимающийся их решением, называетсякомбинаторикой.
Правило суммы:если некоторый объектAможно выбратьmспособами, а объектB–kспособами, причем любой способ выбора объектаAотличен от любого способа выбораB, то выбор «AилиB» можно сделатьm + kспособами.
Правило произведения:пусть объектAможно выбратьmспособами, а после каждого такого выбора другой объектBможно выбрать (независимо от объектаA)kспособами, то пару объектовAиBможно выбратьmkспособами.
Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число (номер элемента) от 1 доn, гдеn– число элементов множества, так что различным элементам соответствуют различные числа.
Различные упорядоченные множества, которые отличаются лишь порядком элементов (т. е. могут быть получены из того же самого множества), называются перестановками. Число возможных перестановок из nэлементов вычисляют по формуле
![]() (31.2)
(31.2)
(читается «n-факториал»).
Конечные упорядоченные подмножества данного множества называются размещениями данного множества.
Число упорядоченных
k-элементных подмножеств
множества, состоящего изnэлементов, т. е.число размещений
изnпо
k обозначают![]() и вычисляют по формуле
и вычисляют по формуле
![]() (31.3)
(31.3)
Произвольное
k-элементное подмножествоn-элементного множества
называетсясочетаниемиз n
элементов по k.
Число сочетаний изn
элементов поk
обозначается![]() и вычисляется по формуле
и вычисляется по формуле
![]()
З а м е ч а н и е 2. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае множества с повторениями вычисляются по другим формулам.
Если среди nэлементов естьn1элементов одного вида,n2элементов другого вида и т. д., точисло перестановок с повторениямиопределяется формулой
![]()
где
![]()
Число размещений поkэлементов с повторениями изnэлементовравноnk, т. е.
![]()
Число сочетаний с повторениями изnэлементов поkэлементовравно числу сочетаний без повторений изn+k–1 элементов поkэлементов, т. е.
![]()
Пример
1.
С помощью таблиц, определяющих A + B,
AB
и
![]() доказать равенство
доказать равенство
![]()
Решение. Составим таблицы, дающие все случаи наступления и ненаступления левой и правой частей доказываемого равенства:
|
A |
B |
|
|
|
|
|
A |
B |
AB |
|
+ |
+ |
– |
– |
– |
+ |
|
+ |
+ |
+ |
|
+ |
– |
– |
+ |
+ |
– |
|
+ |
– |
– |
|
– |
+ |
+ |
– |
+ |
– |
|
– |
+ |
– |
|
– |
– |
+ |
+ |
+ |
– |
|
– |
– |
– |
Последние
столбцы этих таблиц одинаковы, это и
означает справедливость равенства
![]()
Пример 2. Английский математик Карл Пирсон (1857–1936) бросал монету 24 000 раз, причем герб выпал 12 012 раз. Найти относительную частоту выпадения герба в данной серии опытов.
Решение. Относительная частота выпадения герба в данной серии опытов равна:
![]()
Пример 3. Найти вероятность появления верхней грани с числом очков, делящимся на 3, при бросании игральной кости.
Решение. Благоприятствующими данному событию A будут элементарные события A3 и A6 (выпадение 3 и 6), а всего элементарных исходов будет шесть. Поэтому
![]()
Пример 4. В круг радиуса R наудачу брошена точка. Найти вероятность того, что эта точка окажется внутри правильного треугольника, вписанного в данный круг (рис. 31.3).
|
Рис. 31.3 |
Решение. Искомая вероятность равна отношению площади треугольника к площади круга:
|
Пример 5. Определить, сколько двузначных чисел можно записать в десятичной системе счисления.
Решение.
Число десятков двузначного числа может
принимать одно из девяти значений: 1, 2,
3, 4, 5, 6, 7, 8, 9. Число единиц может принимать
одно из десяти значений: 0, 1, 2, 3, 4, 5, 6, 7,
8, 9. Всего получим
![]() двузначных чисел.
двузначных чисел.
Пример 6. Определить, сколькими различными способами могут разместиться на скамейке 6 человек.
Решение. Согласно формуле (31.2) при n = 6, находим
![]()
Пример 7. Определить, сколькими способами можно выбрать четырех человек на четыре различные должности из девяти кандидатов на эти должности.
Решение. Воспользуемся формулой (31.3). При n = 9, k = 4 получаем
![]()
Пример 8. В девятом классе 35 учащихся. Из них нужно выбрать четыре делегата на конференцию. Определить, сколько имеется возможностей такого выбора.
Решение.
![]()
Пример 9. Определить, сколькими способами можно поставить на книжной полке три экземпляра учебника по алгебре, два экземпляра учебника по физике и один экземпляр учебника по белорусскому языку.
Решение.
![]()
Пример 10. Сколько разных пятизначных чисел можно составить из цифр 0, 2, если одна и та же цифра может повторяться несколько раз?
Решение.
Из цифр 0, 2 можем получить
![]() пятизначных чисел. Но числа, записанные
пятью цифрами, первая из которых нуль,
не являются пятизначными.
пятизначных чисел. Но числа, записанные
пятью цифрами, первая из которых нуль,
не являются пятизначными.
Их
столько, сколько четырехзначных чисел
можно составить из цифр 0, 2 при повторении
цифр, т. е.
![]() Поэтому ответ:
Поэтому ответ:![]()
Пример 11. На пяти одинаковых по форме и размеру карточках написаны буквы слова Минск – по одной на каждой карточке. Карточки тщательно перемешаны. Их вынимают наудачу и раскладывают одна за другой на столе. Определить, какова вероятность того, что снова получится слово Минск.
Решение.
Из пяти различных элементов можно
составить P5
перестановок:
![]() Значит, всего равновозможных элементарных
событий будет 120, а благоприятствующих
данному событию – только одно.
Следовательно,
Значит, всего равновозможных элементарных
событий будет 120, а благоприятствующих
данному событию – только одно.
Следовательно,
![]()
Пример 12. В играх на первенство страны по баскетболу участвуют 16 команд, которые будут распределены по жребию на две группы по 8 команд. Какова вероятность того, что две команды-победительницы в промежуточных состязаниях войдут в одну группу?
Решение.
Число всех способов распределения 16
команд на две группы по 8 команд равно
![]() Пусть обе команды-победительницы вошли
в одну группу. К ним следует присоединить
еще 6 любых команд из оставшихся 14. Это
можно сделать
Пусть обе команды-победительницы вошли
в одну группу. К ним следует присоединить
еще 6 любых команд из оставшихся 14. Это
можно сделать![]() способами.
способами.
Отобранные
8 команд можно объявить группой 1,
оставшиеся – группой 2, и наоборот.
Следовательно, требованию задачи
удовлетворяют
![]() комбинаций. Искомая вероятность равна:
комбинаций. Искомая вероятность равна:
![]()
Задания

